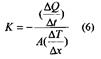|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Viscoelastic deformation
We know that materials generally expand upon heating. This thermal expansion is monitored as an incremental increase in length, ∆L, divided by its initial length, L0. Two unique mechanical responses are found in measuring the thermal expansion of an inorganic glass or an organic polymer (Fig. 6.22). First, there is a distinct break in the expansion curve at the temperature Tg. There are a two different thermal expansion coefficients (slopes) above and below Tg. The thermal expansion coefficient below Tg is comparable to that of a crystalline solid of the same composition. The thermal expansion coefficient above Tg is comparable to that of a crystalline solid of the same composition. The thermal explanation coefficient above Tg is comparable to that for a liquid. As a result, Tg is referred lo as the glass transition temperature.
Below the material is a true glass (a rigid solid), and above Tgit is a super cooled liquid. In terms of mechanical behavior, elastic deformation occurs below Tg,while viscous(liquidlike) deformationoccurs above Tg.continuing to measure thermal expansion above Tgleads to n precipitations drop in the data curve at the temperature Ts.
Fig.6.23. Upon heating, a crystal undergoes modest thermal expansion up to its melting point (Tm), at which a sharp increase in specific volume occurs. Upon further heating, the liquid undergoes a greater thermal expansion. Slow cooling of the liquid would allow crystallization abruptly at Tm and a retracing of the melting plot. Rapid cooling of the liquid can suppress crystallization producing a supercooled liquid. In the vicinity of the glass transition temperature (Tg), gradual solidification occurs. A true glass is a rigid solid with thermal expansion similar to the crystal but an atomic-scale structure similar to the liquid. The viscous behavior of glasses (organic or inorganic) can be described by the viscosity, q, which is defined as the proportionality constant between a shearing force per unit area (F/A) and velocity gradient (dv/dx): F/A = qdv/dx The units for viscosity are traditionally the poise [ = lg/(cm s)], which is equal to 0.1 Pa s.
24. Give definition of Heat capacity and Debye temperature.
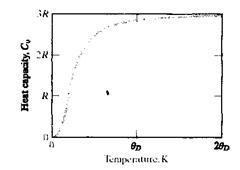
As a material absorbs heat from its environment, its temperature rises. This common observation can be quantified with a fundamental material property, the heat capacity, C, defined as the amount of heat required to raise its temperature by 1K (=1°C): C= Q/∆ Т (1) With Q being the amount of heat producing a temperature change A T. It is important to note that, for incremental temperature changes, the magnitude of ∆ T is the same in either the Kelvin (K) or Celcius (°C) temperature scales. The magnitude of С will depend on the amount of material. The heat capacity is ordinarily specified for a basis of one gram-atom (for elements) or one mole (for compounds) in units of J/g-atom К or J/mol K. A common alternative is the specific heat using a basis of unit mass, such as J/kg K. Along with the heat and the mass, the specific heat is designated by lowercase letters: C= q/m∆ Т (2) There are 2 common ways in which heat capacity (or specific heat) is measured. One is while maintaining a constant volume, Cv (cv), and the other is while maintaining a constant pressure, Cp (cp). The magnitude of Cp is always greater than Cv, but the difference is minor lor most solids at room temperature or below. Because we ordinarily use mass-based amounts of engineering materials under a fixed, ulmospheric pressure, we will tend to use Cp data in this lecture. Fundamental studies of the relationship between atomic vibrations and heat capacity in the early part of the 20-th century led to the discovery that, at very low temperatures, Cv rises sharply from zero al 0 К as Сv = AT3 (3) where A is a temperature-independent constant. Furthermore, above a Debye temperature (ӨD), the value of CV was found to level off at approximately 3R, where R is the universal gas constant. Fig. summarizes how Cv rises to an asymptotic value of 3R above ӨD. As ӨD is below room temperature for many solids and Cp~ Cv, we have a useful rule of thumb for the value of the heat capacity of many engineering materials.
Fig.7.1. The temperature dependence of the heat capacity at constant volume, Cv. The magnitude of Cv rises sharply with temperature near О К and, above the Debye temperature (0D), levels off at a value of approximately 3R. Finally, it can be noted that there are other energy-absorbing mechanisms, besides atomic vibrations, that can contribute to the magnitude of heat capacity.
25. Thermal behavior. Thermal conductivity.
The mathematics for the conduction of heat in solids is analogous to that for diffusion. The analog for diffusivity, D, is thermal conductivity,k, which is defined by Fourier’s law:к - (dQ/dt) / A(dT/dx) (5) where dQ/dt is the rate of heat transfer across an area, A. Due to a temperature gradient dT/dx. Fig. 1. relates the various terms of Eq. (5) and should be compared with the illustration of Fick’s first law.
Fig.1. Heat transfer is defined by Fourier's law (5). The units for к are J/(s m K). For steady-state heat conduction through a flat slab, the differentials of Eq. 7.5 become average terms:
Eq. 6 is appropriate for describing heat flow through refractory walls in high-temperature furnaces. The conduction of heat in engineering materials involves 2 primary mechanisms, atomic vibrations and the conduction of free electrons. For poor electrical conductors such as ceramics and polymers, thermal energy is transported primarily by the vibration of atoms. For electrically conductive metals, the kinetic energy of the conducting (or “free”) electrons can provide substantially more efficient conduction of heat than atomic vibrations. The increasing vibration of the crystal lattice at increasing temperature, then, generally results in a decrease in thermal conductivity. Similarly, the structural disorder created by chemical impurities results in a similar decrease in thermal conductivity. As a result, metal alloy tend to have lower thermal conductivities than pure metals. For ceramics and polymers, atomic vibrations are the predominant source of thermal conductivity, given the very small number of conducting electrons. These lattice vibrations are, however, also wavelike in nature and are similarly impeded by structural disorder. As a result, glasses will tend to have a lower thermal conductivity than crystalline ceramics of the same chemical compositions. In the same way, amorphous polymers will tend to have a greater thermal conductivity than crystalline polymers of comparable compositions. Also, the thermal conductivities of ceramics and polymers will drop with increasing temperature due to the increasing disorder caused by the increasing degree of atomic vibration. For some ceramics, conductivity will eventually begin to rise with further increase in temperature due to radiant heat transfer. Significant amounts of infrared radiation can be transmitted through ceramics, that tend to be optically transparent. The thermal conductivity of ceramics and polymers can be further reduced by the presence of porosity. The gas in the pores has a very low thermal conductivity, giving a low net conductivity to the overall microstructure.
26. Thermal behavior. Thermal expansion.
An increase in temperature leads to greater thermal vibration of the atoms in a material and an increase in the average separation distance of adjacent atoms. In general, the overall dimension of the material in a given direction, L, will increase with increasing temperature, T. This is reflected by the linear coefficient of thermal expansion, α, given by α = dL/LdT (4) with a having units of mm/(mm °C). Note that the thermal expansion coefficients of ceramics and glasses are generally smaller than those for metals, which are, in turn, smaller than those for polymers. The differences are related to the asymmetrical shape of the energy well. The ceramics and glasses generally have deeper wells (i.e., higher bonding energies) associated with their ionic and covalent-type bonding. The elastic modulus is directly related to the derivative of the bonding energy curve near the bottom of the well, and it follows that the deeper the energy well, the larger the value of that derivative and henee the greater the elastic modulus. Furthermore, the stronger bonding associated with deeper energy wells corresponds to higher melting points. The thermal expansion coefficient itself is a function of temperature. 27. Thermal behavior. Thermal shock.
The common use of some inherently brittle materials, especially ceramics and glasses, at high temperatures leads to a special engineering problem called thermal shock. This can be defined as the facture (partial or complete) of the material as a result of a temperature change (usually a sudden cooling). The mechanism of thermal shock can involve both thermal expansion and thermal conductivity. Thermal shock follows from these properties in one or 2 ways. First, a failure stress can be built up by constraint of uniform thermal expansion. Second, rapid temperature changes produce temporary temperature gradients in the material with resulting internal residual stress. More than one furnace design has been flawed by inadequate allowance for expansion of refractory ceramics during heating. Similar consideration must be given to expansion coefficient matching of coating and substrate for glazes (glass coatings on ceramics) and enamels (glass coatings on metals). Even without external constraint, thermal shock can occur due to the temperature gradients created because of a finite thermal conductivity. The surface contracts more than the interior, which is will relatively hot. As a result, the surface “pulls” the interior into compression and is itself “pulled” into tension. With the inevitable presence of Griffith flaws at the surface, this surface tensile stress creates the clear potential for brittle fracture. The ability of a material to withstand a given temperature change depends on a complex combination of thermal expansion, thermal conductivity, overall geometry, and the inherent brittles of that material.
Поиск по сайту: |
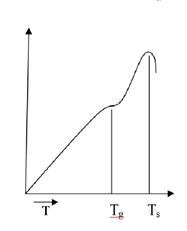 Fig.6.22. Typical thermal expansion measurement of an inorganic glass or an organic polymer indicates a glass transition temperature, Tg, and a softening temperature, Ts.
Fig.6.22. Typical thermal expansion measurement of an inorganic glass or an organic polymer indicates a glass transition temperature, Tg, and a softening temperature, Ts.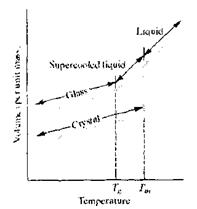 This is the softening temperature and marks the point where the material has become so fluid that it can no longer support the weight of the length-monitoring probe (a small refractory rod).
This is the softening temperature and marks the point where the material has become so fluid that it can no longer support the weight of the length-monitoring probe (a small refractory rod).