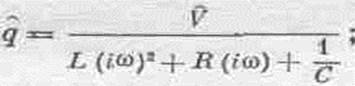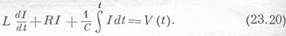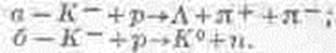Электрический резонанс

Простейшие и самые широкие технические применения резо­нанс нашел в электричестве. Имеется довольно много устройств, из которых собираются электрические цепи. Их часто называют пассивными элементами цепи, и бывают они трех типов, хотя в каждый элемент одного типа всегда примешано чуточку эле­ментов других типов. Прежде чем подробно описать эти элементы, заметим, что наше представление о механическом осцилляторе как о массе, подвешенной к концу пружины, всего лишь приближение. В «массе» сосредоточена вовсе не вся масса системы: пружина тоже обладает какой-то массой, пружина тоже инерционна. Точно так же «пружина» не состоит из одной пружины, масса тоже немного упруга, а не абсолютно тверда, как это может показаться. Подпрыгивая вверх и вниз, она слегка изгибается под толчками пружины. Так же обстоит дело и в электричестве. Расположить все предметы по «элемен­там цепи» с чистыми, идеальными характеристиками можно только приближенно. Так как у нас нет времени обсуждать пре­делы таких приближений, мы просто предположим, что они до­пустимы.

Итак, о трех элементах цепи. Первый называется емкостью (фиг. 23.4); в качестве примера емкости могут служить две ме­таллические пластинки, разделенные тонким слоем диэлект­рика.

Фиг. 23.4. Три пассивных элемента цепи.

Если пластинки зарядить, то между ними возникает раз­ность потенциалов. Та же самая разность потенциалов будет между точками А и В, потому что при любой дополнительной разности потенциалов вдоль соединительных проводов заряды стекут по проводам. Таким образом, заданной разности потен­циалов V между пластинками соответствуют определенные заряды +q и -q на каждой пластинке. Между пластинками существует некое электрическое поле; мы даже вывели соответствующую формулу для него (см. гл. 13 и 14)

V=sd/e₀=qd/e₀A , (23.14)

где d — расстояние между пластинками, А — площадь пласти­нок. Заметим, что разность потенциалов линейно зависит от за­ряда. Если построить емкость не из параллельных пластин, а придать отдельным электродам какую-нибудь другую форму, разность потенциалов будет по-прежнему пропорциональна заряду, но постоянную пропорциональности не так-то легко будет рассчитать. Однако надо знать только одно: разность по­тенциалов между концами емкости пропорциональна заряду V=q/C; множитель пропорциональности равен 1/С (С и есть емкость объекта).

Второй элемент цепи называется сопротивлением; этот эле­мент оказывает сопротивление текущему через него электриче­скому току. Оказывается, что все металлические провода, а так­же многие другие материалы сопротивляются току одинаково; если к концам куска такого материала приложить разность по­тенциалов, то электрический ток в куске I=dq/dt будет пропор­ционален приложенной разности потенциалов

V=RI=R(dq/dt). (23.15)

Коэффициент пропорциональности называют сопротивлением R. Соотношение между током и разностью потенциалов вам, на­верное, уже известно. Это закон Ома.

Если представлять себе заряд, сосредоточенный в емкости, как нечто аналогичное смещению механической системы х, то электрический ток dq/dt аналогичен скорости, сопротивление R аналогично коэффициенту сопротивления g, а 1/С аналогично постоянной упругости пружины k. Самое интересное во всем этом, что существует элемент цепи, аналогичный массе! Это спираль, порождающая внутри себя магнитное поле, когда через нее проходит ток. Изменение магнитного поля порождает на концах спирали разность потенциалов, пропорциональную dI/dt. (Это свойство спирали используется в трансформаторах.) Магнитное поле пропорционально току, а наведенная разность потенциалов (так ее называют) пропорциональна скорости из­менения тока

V=L(dI/dt)=L(d²q/dt²). (23.16)

Коэффициент L — это коэффициент самоиндукции; он является электрическим аналогом массы.

Предположим, мы собираем цепь из трех последовательно соединенных элементов (фиг. 23.5); приложенная между точ­ками 1 и 2 разность потенциалов заставит заряды двигаться по цепи, тогда на концах каждого элемента цепи тоже возникает

разность потенциалов: на концах индуктивности V_L=L(d²q/dt²), на сопротивлении V_R=R(dq/dt), а на емкости V_c=q/C.

Фиг. 23.5. Электрический ко­лебательный контур, состоящий из сопротивления, индуктивности и емкости.

Сумма этих напряжений дает нам полное напряжение

Мы видим, что это уравнение в точности совпадает с механиче­ским уравнением (23.6); будем решать его точно таким же спо­собом. Предположим, что V(t) осциллирует; для этого надо со­единить цепь с генератором синусоидальных колебаний. Тогда можно представить V(t) как комплексное число V, помня, что для определения настоящего напряжения V(t) это число надо еще умножить на exp(iwt) и взять действительную часть. Анало­гично можно подойти и к заряду q, а поэтому напишем уравнение, в точности повторяющее (23.8): вторая производная q— это (iw)²q, а первая — это (iw)q. Уравнение (23.17) перейдет в

или

последнее равенство запишем в виде

где w²₀=1/LC, a g=R/L. Мы получили тот же знаменатель, что и в механической задаче, со всеми его резонансными свойст­вами! В табл. 23.1 приведен перечень аналогий между элект­рическими и механическими величинами.

Таблица 23.1 • МЕХАНИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ВЕЛИЧИНЫ

Еще одно чисто техническое замечание. В книгах по электри­честву используют другие обозначения. (Очень часто в книгах на одну и ту же тему, написанных людьми разных специаль­ностей, используются различные обозначения.) Во-первых, для обозначения Ö-1 используют букву j, а не i (через i должен обозначаться ток!). Во-вторых, инженеры предпочитают соотношение между V и I, а не между V и q. Они так больше привыкли. Поскольку I=dq/dt=iwq, то вместо q можно под­ставить I/iw, и тогда

Можно слегка изменить исходное дифференциальное уравнение (23.17), чтобы оно выглядело более привычно. В книгах часто попадается такое соотношение:

Во всяком случае, мы находим, что соотношение (23.19) между напряжением V и током I то же самое, что и (23.18), и от­личается только тем, что последнее делится на iw. Комп­лексное число R +iwL+1/iwC инженеры-электрики часто называют особым именем: комплексный импеданс Z. Введение новой буквы позволяет просто записать соотношение между током и сопротивлением в виде V=ZI. Объясняется это при­страстие инженеров тем, что в юности они изучали только цепи постоянного тока и знали только сопротивления и закон Ома: V=RI. Теперь они более образованы и имеют уже цепи перемен­ного тока, но хотят, чтобы уравнения были те же самые. Вот они и пишут V=ZI, и единственная разница в том, что теперь со­противление заменено более сложной вещью: комплексным чис­лом. Они настаивают на том, что они не могут использовать принятого во всем мире обозначения для мнимой единицы и пишут j; поистине удивительно, что они не требуют, чтобы вме­сто буквы Z писали букву R! (Много волнений доставляют им разговоры о плотности тока; ее они тоже обозначают буквой j. Сложности науки во многом связаны с трудностями в обозна­чениях, единицах и прочих выдумках человека, о чем сама при­рода и не подозревает.)

Резонанс в природе

Хотя мы детально разобрали вопрос о резонансе в электри­ческих цепях, можно приводить пример за примером из любых наук и отыскивать в них резонансные кривые. В природе очень часто что-нибудь «колеблется» и так же часто наступает резо­нанс. Об этом уже говорилось в одной из предыдущих глав; приведем теперь некоторые примеры. Зайдите в библиотеку, возьмите с полки несколько книг, полистайте их; вы обнаружите кривые, похожие на кривые фиг. 23.2, и уравнения, по­хожие на уравнения, приведенные в этой главе. Много ли най­дется таких книг? Для убедительности возьмем всего пять-шесть книг, и они обеспечат вас полным набором примеров резонансов.

Первые два относятся к механике. Самый первый грандио­зен — речь идет о колебаниях атмосферы. Если бы атмосфера, ко­торая, по нашим представлениям, шарообразна и обволакивает нашу Землю равномерно со всех сторон, под влиянием Луны вы­тянулась бы в одну сторону, то атмосфера приняла бы форму вы­тянутой дыни. Если предоставить атмосферу, имеющую форму дыни, самой себе, то возникнут колебания. Так получается осцил­лятор. Этими колебаниями управляет Луна, которая вращается вокруг Земли. Чтобы понять, как это происходит, представим се­бе, что Луна стоит неподвижно на каком-то расстоянии от Земли, а Земля вращается вокруг своей оси. Поэтому проекция силы, скажем, на ось х имеет периодическую составляющую. Отклик атмосферы на приливно-отливные толчки Луны будет обычным откликом осциллятора на периодическую силу. Кривая bна фиг. 23.6 изображает ожидаемый отклик атмосферы (кривая а приведена на заимствованном нами рисунке из книги Мунка и Мак-Дональда по другому поводу и нас не касается). Может показаться странным, что удалось начертить эту кривую: ведь Земля вращается с постоянной скоростью, и поэтому мож­но получить только одну точку на кривой — точку, приблизи­тельно соответствующую периоду 12 — 12,7 час (приливы бывают дважды в сутки) плюс еще немного, потому что надо учесть движение Луны. Но, измеряя величину атмосфер­ных приливов и время их задержки — фазу, можно найти обе характеристики отклика r и q. По ним можно вычислить w₀ и g а затем начертить уже всю кривую! Вот пример чистой науки. Из двух чисел получают два числа, по этим двум числам чертят очень красивую кривую, которая, конечно, прохо­дит через ту же точку, по которой построена кривая! Кривая эта, конечно, бесполезна, пока нельзя измерить еще чего-нибудь, а в геофизике сделать это зачастую очень трудно. В нашем слу­чае тем, что нужно было бы еще измерить, могут служить колебания атмосферы с собственной частотой w₀; необходимо какое-то возмущение, которое бы заставило атмосферу коле­баться с частотой w₀. Такой случай однажды представился. В 1883 г. произошло извержение вулкана Кракатау, в резуль­тате которого в атмосферу взлетело пол-острова. Взрыв был такой, что удалось измерить период колебаний атмосферы. Он оказался равным 10¹/₂ час. Собственная частота w₀, получен­ная из кривой фиг. 23.6, была равна 10 час 20 мин; таким об­разом было получено по крайней мере хоть одно подтверждение правильности наших представлений об атмосферных приливах.

Фиг. 23.6. Влияние внешнего возбуждения на атмосферу.

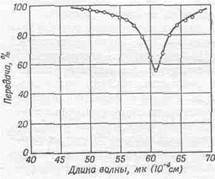
Во втором примере речь пойдет о совсем малых колебаниях. Мы рассмотрим кристалл хлористого натрия, который со­стоит из расположенных друг возле друга ионов натрия и хлора (мы об этом говорили ранее). Ионы эти несут электрический заряд: первый — положительный, второй — отрицательный. Посмотрим, какие интересные колебания могут возникнуть в кристалле. Если отодвинуть все положительные заряды впра­во, а отрицательные — влево и предоставить их самим себе, то они начнут колебаться взад и вперед: решетка ионов натрия против решетки ионов хлора. Но как растащить эти заряды? Очень просто: если внести кристалл в электрическое поле, оно отодвинет положительные за­ряды в одну сторону, а отри­цательные — в другую! Зна­чит, имея внешнее электриче­ское поле, можно, пожалуй, вызвать колебания кристалла. Но для этого частота электриче­ского поля должна быть столь большой, что она соответствует инфракрасному излучению! Таким образом попытаемся построить резонансную кривую, измеряя поглощение инфракрасного света хлористым натрием. Такая кривая изображена на фиг. 23.7.

Фиг. 23.7. Прохождение инфра­красного излучения через тонкую (0,17 мк) пленку поваренной соли.

По абсциссе отложена не частота, а длина волны, но это техни­ческая деталь; между частотой и длиной волны существует стро­го определенное соотношение, так что мы все-таки имеем дело со шкалой частот, и одна из этих частот— резонансная ча­стота.

Ну, а что можно сказать о ширине резонансной кривой? Чем эта ширина определяется? Очень часто кривая выглядит гораздо шире, чем ей предписывается теоретическим значением g (эта ширина называется естественной шириной). Есть две причины уширения резонансной кривой. Мы наблюдаем колеба­ния многих осцилляторов сразу, а их частоты могут немного от­личаться. К этому приводят, например, натяжения в отдельных частях кристалла. Поэтому мы видим сразу много резонансных кривых, проходящих рядом. Они сливаются в одну кривую с большей шириной. Вторая причина очень проста — не всегда можно точно измерить частоту. Сколько со спектрометром ни возись, он всегда зарегистрирует не одну частоту, а целый спектр частот Dw. Поэтому может оказаться, что разрешающая сила спектрометра недостаточна для определения точной формы кри­вой. Так или иначе, но, глядя на фиг. 23.7, трудно сказать, что там за ширина — естественная или та, что соответствует неоднородностям кристалла или разрешающей силе спектрометра.

Еще один пример —более хитрый. Посмотрим, как качает­ся магнит. Если поместить магнит в постоянное магнитное поле, то северный полюс захочет повернуться в одну сторону, а юж­ный — в другую, и если магнит может поворачиваться вокруг оси, он будет колебаться около положения равновесия, как это делает стрелка компаса. Однако магниты, о которых пойдет речь,— это атомы. Они обладают моментом количества движе­ния, и вращение порождает не простое движение в направле­нии поля, а прецессию. Посмотрим со стороны на какую-нибудь составляющую «шатаний», а потом возмутим колебания или по­пробуем управлять ими, чтобы затем измерить поглощение.

На фиг. 23.8 изображена кривая поглощения — типично резонансная кривая.

Фиг. 23.8. Зависимость потери, магнитной энергии в парамаг­нитном органическом соединении от напряженности приложенного поля.

Только получена она немного не так, как предыдущая. Частота горизонтального поля, управляющего ко­лебаниями, все время остается постоянной, хотя, казалось бы, экспериментатор, чтобы получить кривую, должен менять ча­стоту. Можно поступить и так, но технически легче оставить и неизменной, а менять напряженность постоянного поля, что соответствует изменению w₀ в нашей формуле. Таким образом мы имеем дело с резонансной кривой для w₀. Тем не менее мы получаем резонанс с определенными w₀ и g.

Пойдем дальше. Следующий наш пример связан с атомным ядром. Движение протонов и нейтронов в ядре — в некотором смысле колебательное движение. Убедиться в этом можно при помощи такого эксперимента: давайте обстреливать ядра лития протонами. Мы обнаружим, что в ядрах при этом будут происхо­дить какие-то реакции, в результате которых возникает g-излучение. Кривая, изображающая количество испущенного из­лучения, имеет очень острый, типично резонансный максимум. Это изображено на фиг. 23.9. Однако приглядитесь к рисунку повнимательнее: на горизонтальной шкале отложена не частота, как обычно, а энергия! Дело в том, что та величина, которую в классической физике мы привыкли считать энергией, в кван­товой механике оказывается определенным образом связанной с частотой некоторой волны. Если в привычной нам крупномас­штабной физике при анализе какого-нибудь явления приходится иметь дело с частотой, то в квантовомеханических явлениях, связанных с атомным веществом, аналогичные кривые будут зависеть от энергии. Кривая на фиг. 23.9 иллюстрирует эту связь. Размышляя над этой кривой, можно прийти к мысли, что частота и энергия имеют глубокую взаимосвязь; так оно и есть на самом деле.

Вот еще одна резонансная кривая, полученная в результате опытов с атомными ядрами; она очень узкая, уже всех предыду­щих. На фиг. 23.10 величина w₀ соответствует энергии 10 000 эв, а ширина g равна приблизительно 10^-5 эв; иначе говоря, Q=10¹⁰!

Фиг. 23.10. Кривая поглощения g-излучения, полученная Р. Мёссбауэром.

Построив такую кривую, экспериментатор измерил Q самого добротного из ныне известных осцилляторов. Это проделал Р. Мёссбауэр, получивший за свои работы Нобелевскую пре­мию. На горизонтальной шкале отложена скорость, потому что для сдвига частоты использовался эффект Допплера, получаю­щийся в результате относительного движения источника и по­глотителя. Цифры дают некоторое представление о тонкости эксперимента — пришлось измерять скорости в несколько сан­тиметров в секунду! Если продолжить горизонтальную шкалу влево, то нулевую частоту мы найдем на расстоянии 10¹⁰ см! Страницы для этого, пожалуй, не хватит!

Наконец, возьмем какой-нибудь выпуск журнала Physical Review, скажем, за 1 января 1962 г. Найдется ли в нем резонансная кривая? Резонансные кривые имеются непременно в каждом выпуске этого жур­нала, и на фиг. 23.11 изоб­ражена одна из таких кри­вых.

Фиг. 23.11. Зависимость эф­фективных сечений реакций от величины момента количества дви­жения.

Нижняя кривая описывает нерезонанс­ный фон; верхняя кривая показывает, что на зтот фон наложено резонансное сечение.

Это очень интересная кривая. Она соответствует ре­зонансу в реакциях со стран­ными частицами (K^--мезоны и протоны). Резонанс был об­наружен при измерении ко­личества частиц разных сор­тов, получающихся в резуль­тате реакции. Разным про­дуктам реакции соответствуют разные кривые, но в каждой из них при одной и той же энергии есть пики примерно одинаковых очертаний. Зна­чит, при определенной энергии K^--мезона существует резо­нанс. При столкновении К^--мезонов и протонов, наверное, создаются благоприятные для резонанса условия, а может быть, даже новая частица. Сегодня мы еще не можем сказать, что такое эти выбросы в кривых — «частица» или просто ре­зонанс. Очень узкий резонанс соответствует очень точно от­меренному количеству энергии; это бывает тогда, когда мы имеем дело с частицей. Когда резонансная кривая уширяется, то становится трудно сказать, с чем мы имеем дело — с части­цей, которая живет очень мало, или просто с резонансом в реак­ции. В гл. 2 мы отнесли эти резонансы к частицам, но когда писалась та глава, об этом резонансе еще не было известно, по­этому нашу таблицу элементарных частиц можно дополнить!

Глава 24

ПЕРЕХОДНЫЕ РЕШЕНИЯ

Энергия осциллятора

Затухающие колебания

Поиск по сайту: