 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Закон додавання швидкостей
Нехай у системі К рухається матеріальна точка з координатами x(t). y(t) і z(t). Ця ж сама точка в системі К' описується координатами x'(t'), y'(t'), z'(t'). Продиференціюємо координату х' за t'. щоб знайти швидкість точки и'x у системі K'. Користуємось оберненими перетвореннями (12§1) :
З перетворень (12§1) неважко обчислити похідну dt'/dt:
Підставляючи її в (1) маємо:
до вирази для и'у та u'z отримано цілком аналогічним способом. Зовсім неважко записати вирази для зворотного перо-ходу:
Відмітимо, що в нерелятивіському випадку, V/c —> 0. перетворення СТВ для швидкостей (3) мають вигляд класичних перетворень Галілея (5) . В іншому граничному випадку. V —> с. формула (3) забезпечує граничний характер швидкості світла с. Отже, швидкість, згідно з перетвореннями Лоренца, завжди не перевищує швидкості світла. Тут слід підкреслити, що цей результат не означає, шо в СТВ ніякі швидкості не перевищують с. СТВ стверджує лито. І по з надсвітловими швидкостями неможливо передати інформацію. Так, наприклад, фазова швидкість хвилі (але не групова), швидкість світлового «зайчика» можуть бути як завгодно більше за с. Механіка СТВ Геометрія 4—простору Отримавши перетворення Лоренца, ми пересвідчились у тому, що світ, який нас оточує, має в дійсності чотири виміри (r,ct), ане три. Щоправда, відмінності трьохвимірної геометрії від чотирьохвимірної стають суттєвими лише при швидкостях, які можна порівнювати зі швидкістю світла. Проте нас турбує зараз лише принципова сторона цього питання. А навіщо таку геометрію будувати? Причин, принаймні, дві. Перша — ця геометрія є об'єктивно існуючою, ми в цьому 4-просторі живемо, хоча до цього часу це не усвідомлювали. Є й друга причина. Звичайно, можна було б просто користуватись перетвореннями Лоренца і безпосередньо показати, що рівняння Максвелла відносно цих перетворень інваріантні. Але це далеко не найкращий вихід, бо крім рівнянь Максвелла є інші рівняння — Шредінгера, Дірака та ін. А якщо нам потрібно записати деякі рівняння так, щоб вони гарантовано були б лоренц-інваріантні? Очевидно, треба йти шляхом, який вибирали при побудові векторного числення. Справа в тому, що векторна форма запису є спосіб зображення векторних величин незалежно від перетворення системи координат (зсуву, повороту тощо). Наприклад, вирази M=r×p, B= не залежать від перетворень системи координат (на відміну від покоординатної форми запису). Для трьохвимірного випадку ми побудували цілу низку понять, що можуть входити в ліву та праву частини рівності.
Оскільки всі ці величини при повороті системи координат змінюються однаковим чином, то в цілому рівняння не змінюються і від простих перетворень координат фізичний результат не залежить. Аналогічним чином введемо систему понять для 4-простору. Тоді, якщо показати, що деяке рівняння містить лише об'єкти чотирьохвимірного простору, то воно гарантовано буде лоренц-інваріантним. Крім того, маючи відповідний набір чотирьохвимірних об'єктів, ми зможемо будувати нові рівняння, що будуть лоренц-інваріантними. Звертаємо увагу, що на відміну від евклідової геометрії у чотирьохвимірному просторі-часі мірою довжини є інтервал:
Нагадаємо, що в евклідовому 4-просторі такою мірою є:
де ω — четверта координата. Відмінність очевидна, але ці дві геометрії мають багато спільного. Введемо низку правил та означень, якими будемо користуватись, не виконуючи докладних обґрунтувань.
1.Сукупність координат події будемо вважати компонентами чотирьохвимірного радіус-вектора (вектор у чотирьохвимірному просторі) та позначати:
Часто також використовують позначення 2. Квадрат довжини цього вектора, як ми вже бачили, дорівнює:
Ця величина не змінюється при довільних поворотах чотирьохвимірної системи координат. Зокрема такими поворотами є й перетворення Лоренца. Не потребує спеціального доведення той факт, що координатна частина інтервалу не змінюється при звичайних трьохвимірних поворотах навколо початку координат. 3. Зрозуміло, що 4-вектором може бути не лише сукупність координат деякої події. З геометричного погляду сукупність чотирьох чисел, що при довільних поворотах системи координат (включаючи і перетворення Лоренца) змінюється так само як і,
Квадрат довжини довільного 4-вектора, очевидно, є величиною, що не змінюється при переходах (та поворотах) від однієї системи координат до іншої,
4. Для зручності запису вводять два типи величин: з індексами зверху Ai (контраваріантні) таз індексами внизу Визначимо зв'язок між коваріантними та контраваріантними компонентами 4-вектора наступним правилом:
Отже діє правило: підняття або опускання просторових індексів не змінює знак компоненти, а переміщення часового індексу змінює знак на протилежний. Перехід від контра- до коваріантних компонент вектора можна подати в такому вигляді:
Використовуючи ці позначення квадрат 4-вектора набуває форми:
У цих та аналогічних виразах прийнято знак суми не писати, а мати на увазі, що якщо індекс повторюється двічі (один раз внизу і один раз вверху), то за ним необхідно взяти суму від 1 до 4. Такі індекси звуть німими. Для ортогональних некосокутних координат різниці між коваріантними та контраваріантними величинами немає. Для координат косокутних різниця полягає в тому, що коваріантні компоненти утворюються при проектуванні точки шляхом опущення перпендикуляра, а контраваріантні — шляхом паралельного переносу (див. рис. 5.3).
Використовуючи коваріантні та контраваріантні позначення, можемо записати основну властивість 4-вектора (6) у вигляді:
Тобто, якщо при поворотах системи координат (включаючи і лоренцеві), деяка сукупність чотирьох величин перетворюється вищезазначеним чином, то вона має право називатись вектором чотирьохвимірного простору. Вираз для матриці
5. Аналогічно до трьохвимірного випадку вводять поняття скалярного добутку:
Взагалі, у парі німих індексів верхній та нижній індекс можемо змінювати місцями. Введений таким чином скалярний добуток є скаляр і не змінюється при довільних поворотах системи координат.
6.Квадрат 4-вектора може бути додатним, від'ємним та дорівнювати нулеві. Відповідно до цього будемо називати 4-вектори просторовоподібними , часоподібними або нульовими.
7.Просторові компоненти 4-вектора утворюють звичайний 3-вектор А. Відносно трьохвимірного простору компонента А4 є скаляр. Квадрат 4-вектора часто позначають таким чином:
8. Аналогічно до трьохвимірного випадку 4-тензором другого рангу називають сукупність 16 величин, які при перетвореннях координат перетворюються на добуток двох 4-векторів:
9.Компоненти 4-тензора другого рангу можуть бути зображені у вигляді контраваріантному
10.Компоненти 11.Тензор 12.Найважливіше правило, яким постійно користуються при обчисленнях: у всякій тензорній (зокрема і векторній) рівності вирази в обох частинах повинні містити однакові й однаково розташовані вільні індекси (до німих індексів це, звичайно, не відноситься). Вільні індекси можемо переміщувати вверх або вниз, але обов'язково одночасно у всіх частинах рівності. Прирівнювати коваріантні та контрваріантні величини не можна. Один з простіших тензорів другого рангу це так званий матричний тензор:
Переходячи до іншої інерціальної системи координат за правилом (8), переконуємося, що цей тензор незмінний, тобто він є інваріант відносно перетворень Лоренца. За допомогою метричного тензора зв'язок між коваріантними та контраваріантними компонентами 4-векторів набуває вигляду
Очевидно, що:
Поиск по сайту: |
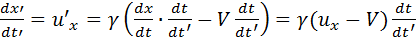 (1)
(1)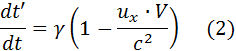

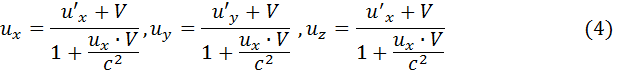
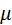 H (1)
H (1)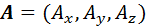
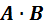
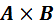
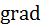 ϕ
ϕ
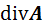
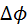
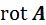
 (2)
(2)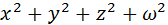 (3)
(3) ,
, 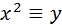 ,
, 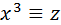 ,
, 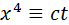 (4)
(4)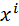 = (x,y,z,ct), або
= (x,y,z,ct), або  (5)
(5) називають чотирьохвимірним вектором {4-вектором) і позначають Аi = (А, А4). Закон перетворення має вигляд:
називають чотирьохвимірним вектором {4-вектором) і позначають Аi = (А, А4). Закон перетворення має вигляд: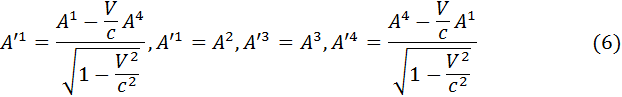
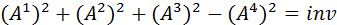 (7)
(7)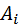 (коваріантні).
(коваріантні). ,
, 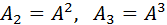 ,
,  (8)
(8)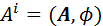 ,
,  (9)
(9) (10)
(10)


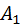 x
x
 або
або 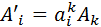 (11)
(11) легко записати безпосередньо з перетворень Лоренца:
легко записати безпосередньо з перетворень Лоренца: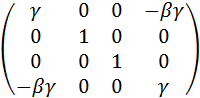 (12)
(12)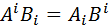 =
= 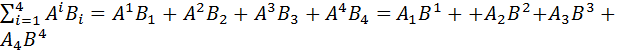 (13)
(13)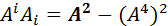 (14)
(14)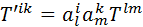 (15)
(15)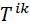 , коваріантному Тік або змішаному
, коваріантному Тік або змішаному 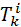 . При цьому діє загальне правило: підняття або опускання просторових індексів не змінює знак компоненти, а переміщення часового індексу змінює знак на протилежний:
. При цьому діє загальне правило: підняття або опускання просторових індексів не змінює знак компоненти, а переміщення часового індексу змінює знак на протилежний: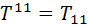 ,
, 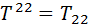 ,
, 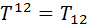 ,
, 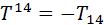 ,
, 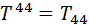 (16)
(16)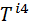 та
та 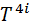 (і =1,2,3) утворюють 3-вектори. Компонента Т44 відносно трьохвимірного простору є скаляр.
(і =1,2,3) утворюють 3-вектори. Компонента Т44 відносно трьохвимірного простору є скаляр. та антисиметричним, якщо
та антисиметричним, якщо  . В антисиметричного тензора всі діагональні компоненти нулеві (покажіть самостійно).
. В антисиметричного тензора всі діагональні компоненти нулеві (покажіть самостійно). (17)
(17)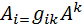
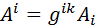 (18)
(18) (19)
(19)