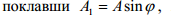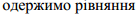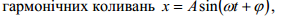|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Динамічний коефіцієнт при ударі
дарне прикладення навантаження до пружної системи приводить до значного зростання напружень і переміщень у порівнянні із статичним прикладенням такого ж навантаження. Це збільшення оцінюється динамічним коефіцієнтом КД , що показує, у скільки разів напруги і переміщення при динамічному впливі навантаження будуть більше, ніж при статичному її прикладенні.
При згинальному ударі (рис.4.16)
σД = КД·σст; fД = КД·fст,
де σст і fст - напруга і прогин при статичному прикладенні сили Р;
σД і fД - ті ж величини при динамічному впливі сили Р.
Наближена теорія удару виходить з того, що кінетична енергія падаючого вантажу цілком переходить у потенційну енергію деформації балки.
Вплив маси пружної системи на деформації і напруження при ударі Якщо власна вага стержня Q і вага падаючого вантажу P (рис.12.1) – величини одного порядку, то інерцію маси стержня слід враховувати, оскільки це може суттєво вплинути на результати розрахунків. Якщо стержень безмасовий
Якщо врахувати масу стержня, але привести її до місця удару, то
де Розділивши (12.17) на (12.16), отримаємо поправку
тоді формула динамічного коефіцієнта із врахуванням маси стержня набуде вигляду
Міцність матеріалів при ударному навантаженні. Ударна в’язкість При ударі, внаслідок того що швидкості навантаження великі, утворення і розвиток пластичної деформації матеріалу зразка чи деталі утруднене. Тому значення Ударну в’язкість
де Т1 ,Т2 – покази вимірювального пристрою маятникового копра (Н/м). Вільні коливання стержня з одним ступенем вільності Розглянемо вільні (власні) поздовжні коливання системи, що складається з прямого стержня довжиною A і закріпленого на кінці вантажу вагою Q і масою m . Позначимо :δст – статичне видовження стержня, спричинене вантажем Q . Одержимо диференційне рівняння вільних коливань Розв”язком рівняння є Вводячи замість сталих
Вимушені коливання систем з одним ступенем вільності Напруження в циліндричній системі координат
Поиск по сайту: |

 .
.
 ,
,
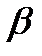 - коефіцієнт приведення розподіленої маси стержня до точки удару.
- коефіцієнт приведення розподіленої маси стержня до точки удару. , яку треба внести до формули (12.6)
, яку треба внести до формули (12.6)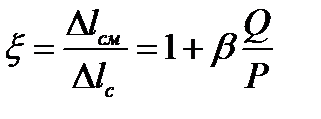 ,
,
 .
.
 і
і  матеріалу підвищуються, натомість різко знижуються його характеристики пластичності
матеріалу підвищуються, натомість різко знижуються його характеристики пластичності визначають як роботу
визначають як роботу  , затрачену на руйнування зразка при ударному згині, віднесену до робочої площі його поперечного перерізу
, затрачену на руйнування зразка при ударному згині, віднесену до робочої площі його поперечного перерізу  .
.