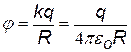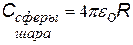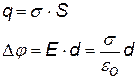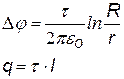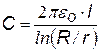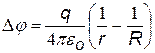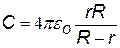|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Проводники в электростатическом поле
При внесении незаряженного проводника во внешнее электростатическое поле на его поверхности появляются заряды. Явление перераспределения зарядов в проводнике при внесении его во внешнее электростатическое поле, называется электростатической индукцией (наведением зарядов, электризацией посредством наведения).
3) Величина наведенного (индуцированного) заряда всегда меньше величины наводящего заряда. Только в случае, когда наводящий заряд находится внутри металлической полости, наведенный заряд оказывается таким же по величине, но при этом поверхностная плотность зарядов оказывается различной. На рисунке: точечный заряд окружен незаряженным металлическим полым телом. И внутренняя и внешняя поверхности сферические, но центры их смещены. На внешней поверхности индуцированный заряд распределяется равномерно, а на внутренней – сложным образом. 4) Наведенные заряды влияют на электрическое поле наводящих зарядов. 5). Индуцированный заряд возникает и на уже заряженном теле. Если рядом находятся два положительных заряда +Q и +q, они должны отталкиваться. Но наведенный отрицательный заряд на одном из зарядов может оказаться бόльшим, чем его собственный заряд, и заряды будут притягиваться друг к другу.
Электроемкость. Все проводники обладают свойством накапливать электрические заряды. Это свойство называется электроемкостью. Количественная характеристика этого свойства также называется электроемкостью [10] и обозначается С. Различают электроемкость уединенного проводника (собственная емкость), находящегося вдали от других проводников, и взаимную емкость системы из двух и более проводников.
Фарада – единица измерения емкости в СИ - является чрезвычайно большой величиной. Так, емкость земного шара примерно 7×10-4 Ф, поэтому обычно пользуются микро-, нано- и пикофарадами. Собственная емкость зависит только от формы и размеров проводника и от диэлектрических свойств окружающей среды (вакуум, воздух, керосин,…) и не зависит ни от материала проводника (Fe, Cu, Al,…), ни от того, заряжен он или нет.[11] Каждый уединенный проводник обладает «своей» емкостью, если, например, изогнуть кусок проволоки или сделать вмятину в шарике, их емкость изменится. Вычисление емкости представляет собой сложную математическую задачу, и если проводник имеет сложную конфигурацию, то аналитически эта задача не решается. Вычислим электроемкость уединенной сферы (шара).
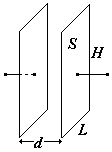
Взаимная емкость также зависит от формы и размеров проводников и, кроме того, от их взаимного расположения. Система из двух проводников называется конденсатором в том случае, когда расстояние между ними достаточно мало, и электрическое поле (когда они заряжены) сосредоточено в основном между проводниками. Сами проводники при этом называют обкладками. Вычислить емкость такой системы можно для обкладок простей формы: плоских, сферических и цилиндрических (без учета краевых эффектов). Вычислим емкость плоского конденсатора – это две металлические параллельные пластины (обкладки) одинаковых размеров, разделенные слоем диэлектрика (вакуум, воздух и др.). Если расстояние между пластинами значительно меньше размеров пластин: d << L, H, поле между пластинами можно считать однородным. В действительности вблизи краев пластин поле неоднородно (см. рис., на котором показана половина плоского конденсатора, линии со стрелками – это силовые линии, без стрелок – эквипотенциальные поверхности). Учесть эти краевые эффекты трудно.
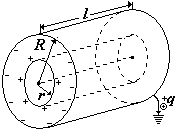
Цилиндрический конденсатор. Это два соосных металлических цилиндра, в промежутке между которыми – диэлектрик (вакуум, воздух и др.). Длина цилиндров-обкладок l, радиусы R и r (см. рис.). Если сообщить внутренней обкладке заряд +q, на внешней обкладке индуцируются заряды -q и +q, положительный заряд с внешней поверхности наружной обкладки уводится в землю. Поле конденсатора в основном сосредоточено между обкладками, если расстояние между ними (R - r) << l. Краевые эффекты не учитываем.
Сферический конденсатор. Это две металлические концентрические сферы, разделенные сферическим слоем диэлектрика. Если внутренней обкладке сообщить заряд +q, на внутренней поверхности внешней обкладки индуцируется заряд -q, а на внешней ее поверхности +q. Этот заряд отводится в землю за счет заземления (см. рис.). Поле такого конденсатора сосредоточено только между обкладками.
Поиск по сайту: |
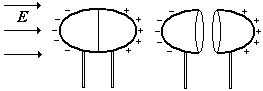 1) Если в поле внести незаряженный металлический проводник из двух контактирующих частей, на их поверхностях возникнут индуцированные заряды. Если эти части развести с помощью изолирующих ручек, то каждая часть окажется заряженной соответствующим зарядом (см. рис.). При этом напряженность поля внутри проводников всегда равна нулю.
1) Если в поле внести незаряженный металлический проводник из двух контактирующих частей, на их поверхностях возникнут индуцированные заряды. Если эти части развести с помощью изолирующих ручек, то каждая часть окажется заряженной соответствующим зарядом (см. рис.). При этом напряженность поля внутри проводников всегда равна нулю.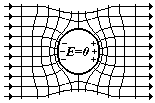 2) Незаряженный проводник, внесенный в электростатическое поле искажает поле (см. рис.- линии со стрелками – силовые линии внешнего однородного поля; перпендикулярные им линии – это эквипотенциальные поверхности; ± - обозначены наведенные заряды).
2) Незаряженный проводник, внесенный в электростатическое поле искажает поле (см. рис.- линии со стрелками – силовые линии внешнего однородного поля; перпендикулярные им линии – это эквипотенциальные поверхности; ± - обозначены наведенные заряды).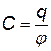 (фарада) (§)
(Ф = Кл/В)
(фарада) (§)
(Ф = Кл/В)
 (§§)
(§§)