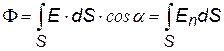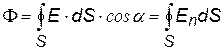|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Графическое изображение электростатического поля
Электростатическое поле удобно изображать графически с помощью силовых линий и эквипотенциальных поверхностей.
1) Силовые линии непрерывны. Они имеют начало и конец – начинаются на положительных и заканчиваются на отрицательных зарядах. 2) Силовые линии не могут пересекаться друг с другом, т.к. напряженность – это сила, а две силы в данной точке от одного заряда не могут быть. 3) Силовые линии проводят так, чтобы их количество через единичную перпендикулярную площадку было пропорционально величине напряженности. 4) Силовые линии «выходят» и «входят» всегда перпендикулярно поверхности тела. 5) Силовую линию не следует путать с траекторией движущегося заряда. Касательная к траектории совпадает с направлением скорости, а касательная к силовой линии – с силой и, следовательно, с ускорением. Эквипотенциальной поверхностьюназывают поверхность, в каждой точке которой потенциал имеет одинаковое значение j = const. Силовые линии всегда перпендикулярны эквипотенциальным поверхностям. Докажем это. Пусть вдоль эквипотенциальной поверхности перемещается точечный заряд q. Элементарная работа, совершаемая при этом равна dA=qE×cosa×dl = q×dj = 0, т.к. dj = 0. Поскольку q ,E и ×dl ¹ 0, следовательно cosa = 0 и a = 90о .
Принцип суперпозиции. На основе опытных данных был получен принципа суперпозиции (наложения) полей: «Если электрическое поле создается несколькими зарядами, то напряженность и потенциал результирующего поля складываются независимо, т.е. не влияя друг на друга». При дискретном распределении зарядов напряженность результирующего поля равна векторной сумме, а потенциал алгебраической (с учетом знака) сумме полей, создаваемых каждым зарядом в отдельности. При непрерывном распределении заряда в теле векторные суммы заменяется на интегралы, где dE и dj– напряженность и потенциал поля элементарного (точечного) заряда, выделенного в теле. Математически принцип суперпозиции можно записать так.
В качестве примера получения выражения для напряженности поля с помощью принципа суперпозиции найдем напряженность поля тонкого стержня конечной длины, равномерно заряженного с линейной плотностью заряда t Выберем бесконечно малый элемент dl стержня с зарядом dq. Поскольку напряженности от различных элементов направлены по-разному, введем оси проекций х и у. Итегрируя, найдем результирующие напряженности Ех и Еу.
Этот пример показывает, что вычисление напряженности полей представляет собой достаточно сложную задачу даже в нашем случае, когда мы не учитывали поле вблизи концов стержня. Основной задачей электростатики является вычисление полей заряженных тел. Найти напряженность поля заряженного тела можно с помощью: 1) принципа суперпозиции - это сложная математическая задача, решаемая только в некоторых простых случаях или 2) теоремы Гаусса, которая упрощает расчеты, но только в случае бесконечной плоскости, бесконечной нити (цилиндра) или сфер и шаров (см. ниже). Теорема Гаусса. Сначала введем понятие «поток вектора» - это скалярная величина
Поиск по сайту: |
 Силовая линия – это линия, в каждой точке которой касательная совпадает с направлением вектора напряженности (см. рис.). Силовым линиям придают направление стрелкой. Свойства силовых линий:
Силовая линия – это линия, в каждой точке которой касательная совпадает с направлением вектора напряженности (см. рис.). Силовым линиям придают направление стрелкой. Свойства силовых линий:

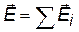



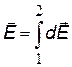
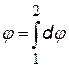
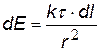
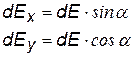





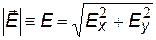
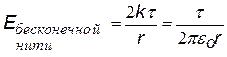
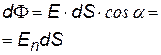 (Н×м2/Кл = В×м)
(Н×м2/Кл = В×м)