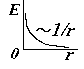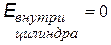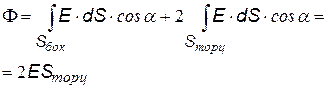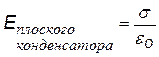|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Применение теоремы Гаусса
Чтобы найти напряженность с помощью теорем Гаусса, нужно взять интеграл. А как его взять, если мы Е еще только пытаемся найти? Кроме того, под интегралом «мешает» cosa. Надо суметь выбрать такую замкнутую поверхность (ее удобно называть гауссовой), в каждой точке которой было бы Е = const, и cosa = const. Тогда в левой части теоремы Е и cosa можно будет вынести из-под знака интеграла. Поэтому практически теорему Гаусса можно применить только в следующих случаях: сфера, шар, длинная нить, длинный цилиндр, бесконечная плоскость. 1) Сфера,заряженная с поверхностной плотностью заряда s (Кл/м2) Рассмотрим области : 1) вне сферы (
2)Тонкая длинная нить,заряженная с линейной плотностью заряда t (Кл/м) В этом случае «гауссова» поверхность – соосный с нитью цилиндр длиной l. Сначала найдем поток, потом воспользуемся теоремой Гаусса.
3) Тонкостенный длинный цилиндр, заряженный: 1) с линейной плотностью заряда t или 2)с поверхностной плотностью заряда s. Этот пример аналогичен предыдущему. Выбираем гауссову поверхность в виде соосного цилиндра, разбиваем поверхность на боковую и две торциальные. В первом случае при заданной линейной плотности t получим такую же формулу, как идля длинной нити. Во втором случае охватываемый заряд равен (s×2p×R×l) и формула для E несколько иная, хотя зависимость от r – та же.
4) Плоскость, бесконечно протяженная, заряженная с поверхностной плотностью заряда s. Выберем гауссову поверхность S в виде цилиндра, перпендикулярного заряженной плоскости. Высота цилиндра (2×х/2). [9] Разобьем поверхность на боковую и две торцевых.
5) Две плоскости, параллельные, разноименно заряженные (плоский конденсатор). В этом случае напряженность поля можно найти по принципу суперпозиции, зная напряженность поля одной плоскости:
Поиск по сайту: |
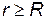 ) и внутри ее (
) и внутри ее ( 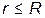 ). Выберем поверхности: 1) S1 и 2) S2 – обе поверхности – сферы, концентрические с заряженной сферой. Сначала найдем потоки вектора Е через выбранные поверхности, а затем воспользуемся теоремой.
). Выберем поверхности: 1) S1 и 2) S2 – обе поверхности – сферы, концентрические с заряженной сферой. Сначала найдем потоки вектора Е через выбранные поверхности, а затем воспользуемся теоремой. (¨)
(¨)


 (¨¨)
(¨¨)


 q = s×2pR2 – полный заряд сферы
q = s×2pR2 – полный заряд сферы