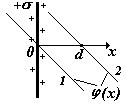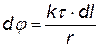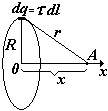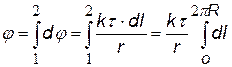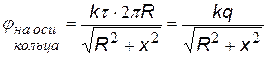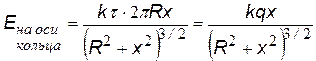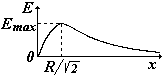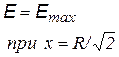|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Потенциалы полей различных заряженных тел
Будем рассматривать только случаи, когда напряженность и потенциал зависят только от одной координаты х или радиальной координаты r для сферически или цилиндрически симметричных тел. Разность потенциалов связана с напряженностью в этом случае как (см. формулу (···)):
Из уравнений (ª) или (···) можно найти разность потенциалов, если известна функция Е(r) или Е(r). Чтобы получить формулу для потенциала, следует выбрать уровень нулевого потенциала (так же, как в случае потенциальной энергии – см. механику). Обычно принимают j = 0 на бесконечности, но для поля нити это невозможно (см. ниже). Точечный заряд. Подставим в формулу (ª) выражение для напряженности поля точечного заряда. 1 и 2 – любые две точки на радиальной оси координат r. Примем j 1 = 0 при r1 ®¥, заменим j 2 ® j , r2 ®r получим j (r).
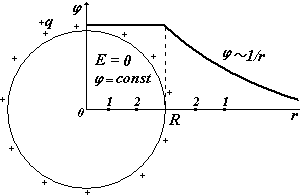
2).Сфера радиуса R, заряженная с поверхностной плотностью заряда s (Кл/м2). Полный заряд на сфере q = s×4p×R2 . Будем рассматривать две области:1)
3)Бесконечно длинная нить, заряженная с линейной плотностью заряда t. Выберем на оси радиальных координат r две любые точки с координатами r1 и r2. (см. рис.). Подставим в (ª) напряженность поля длинной нити и проинтегрируем.
4)Бесконечно протяженная плоскость, равномерно заряженная с поверхностной плотностью заряда s (Кл/м2). Выберем на оси координат х две произвольные точки х1 и х2 .). Используем формулу связи Е и j (···), подставим выражение для напряженности поля бесконечной плоскости.
Следует иметь в виду, что формулы для Е и j в случаях плоскости, нити, цилиндра применимы только на расстояниях от них, существенно меньших размеров этих тел. В действительности при учете краевых эффектов поля становятся более сложными. Во всех случаях, задавая нулевой уровень потенциала j = 0 в различных точках, мы можем получить сколько угодно формул для потенциала данного поля. Потенциальные кривые (или прямые), т.е. графики j(r)или j(х) при этом будут перемещаться по вертикали параллельно самим себе. В принципе, неважно, где выбрать нулевой уровень потенциала, т.к. во всех задачах имеет значение не сам потенциал, а его изменение Так как потенциал – скалярная величина, а напряженность – вектор, то значительно проще найти сначала зависимость j(r) или j(х), затем дифференцируя, получить формулу для Е(r)или Е (х). В качестве примера найдем потенциал поля на оси тонкого кольца, равномерно заряженного с линейной плотностью t, а затем Е (х).Для этого выделим в кольце бесконечно малый элемент dl с зарядом dq = t×dl (см. рис.) В некоторой точке A потенциал складывается из потенциалов, создаваемых всеми элементами кольца.
Поиск по сайту: |
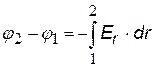 (ª)
(ª)
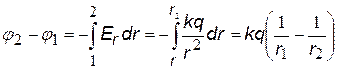
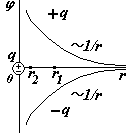
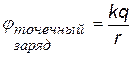 (при j¥ = 0)
(при j¥ = 0)
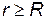 - выбираем две любые точки 1 и 2 в этой области и 2)
- выбираем две любые точки 1 и 2 в этой области и 2) 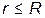 также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т.к. по смыслу j - потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.
также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т.к. по смыслу j - потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.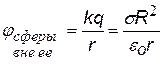 (при j¥ = 0)
(при j¥ = 0)
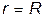
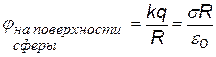

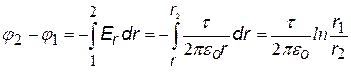
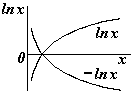 j 1 = 0 при r1 = r0,
заменим j 2 ® j , r2 ®r получим
j (r)
j 1 = 0 при r1 = r0,
заменим j 2 ® j , r2 ®r получим
j (r)
 j = 0 при r = r0
j = 0 при r = r0


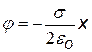 j = 0 при х = 0
2)
j = 0 при х = 0
2)  j = 0 при х = d
j = 0 при х = d