 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Движущиеся синхронизированные часы с точки зрения неподвижного наблюдателя
При анализе парадокса близнецов и решении многих других задач по релятивизму известную трудность вызывает тот факт, что показания часов движущейся системы, синхронизированных в этой системе, для неподвижного наблюдателя представляются различными. Остановимся на этом эффекте подробнее.
Вернемся снова к точке зрения земного наблюдателя. Пусть часы a и b принадлежат подвижной системе и они синхронизированы в этой системе. Когда часы b проходят над наблюдателем B часы a проходят над наблюдателем A. Пусть кроме того часы земного наблюдателя начали свой отсчет в тот момент, когда часы b проходили над наблюдателем A. Тогда в тот момент, когда часы b пройдут над пунктом B, часы земного и космического наблюдателя будут показывать соответственно В этот же момент над наблюдателем A проходят часы подвижной системы координат t2. Иначе можно сказать, что часы t2 прошли над наблюдателем A, когда его часы показывали время Запишем оба выражения рядом: Видно, что с точки зрения земного наблюдателя подвижные синхронизированные часы показывают разное время. Найдем разницу в их показаниях. Запомним этот результат.
Если двое синхронизированных в своей системе отсчета часов t1 и t2 движутся относительно неподвижной системы со скоростью Та же самая разница по часам неподвижного наблюдателя будет равна При этом отстающие часы показывают опережающее время: t2 > t1. Еще одно полезное замечание. Из полученных выражений видно, что если наблюдатель на Земле будет следить за часами удаляющегося наблюдателя, то заметит, что они отстают от его часов: Теперь вернемся к задаче о близнецах и решим ее еще одним способом.
Поиск по сайту: |

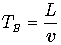 ,
, 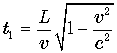 .
.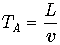 . Теперь перейдем в подвижную систему координат. С точки зрения подвижного наблюдателя все его часы показывают одно и то же время. Кроме того ему известно, что в момент встречи часов t2 и наблюдателя A, часы наблюдателя A показывали время
. Теперь перейдем в подвижную систему координат. С точки зрения подвижного наблюдателя все его часы показывают одно и то же время. Кроме того ему известно, что в момент встречи часов t2 и наблюдателя A, часы наблюдателя A показывали время 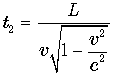 . Именно этот результат и должен увидеть земной наблюдатель в пункте A.
. Именно этот результат и должен увидеть земной наблюдатель в пункте A.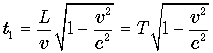 ,
, .
. , где
, где  .
.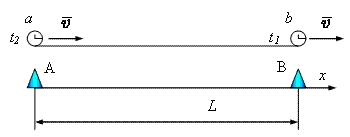
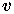 , а расстояние между ними равно L в неподвижной системе, то они показывают разное время. Причем
, а расстояние между ними равно L в неподвижной системе, то они показывают разное время. Причем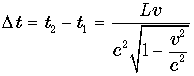 , где
, где 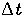 – разница в показаниях подвижных часов.
– разница в показаниях подвижных часов.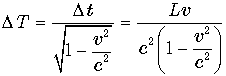 .
.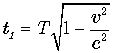 . А если он будет следить за часами движущейся системы, которые проносятся непосредственно над ним, то эти часы будут опережать время на Земле:
. А если он будет следить за часами движущейся системы, которые проносятся непосредственно над ним, то эти часы будут опережать время на Земле: 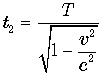 .
.