 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ІНТЕГРУВАННЯ ІРРАЦІОНАЛЬНИХ ФУНКЦІЙ
Розглянемо інтеграли від деяких простіших ірраціональних функцій, які за допомогою певних підстановок можна звести до інтегралів від раціональних функцій.
Інтеграли виду
де
Такі інтеграли раціоналізуються підстановкою
де
Дійсно,
де Приклад 6.1. Знайти інтеграли
1)
3)
Розв’язання.
1) Найменшим спільним кратним знаменників дробів
НСК(2,3) = 6. Тому застосуємо підстановку
2) Представимо даний інтеграл у вигляді:
Найменшим спільним кратним знаменників дробів
Виділимо цілу частину
3)
Запишемо розклад підинтегральної функції на елементарні дроби:
Таким чином,
Повернемося до змінної
4)
Одержано інтеграл від неправильного раціонального дробу. Виділяючи цілу частину, маємо
Для знаходження останнього інтегралу запишемо розклад підинтегральної функції на елементарні дроби:
звідки
Маємо,
Повертаючись до змінної
Інтеграли виду
де
Такі інтеграли раціоналізуються підстановкою
де
Приклад 6.2. Знайти інтеграли
1)
Розв’язання.
1) Введемо підстановку Виразимо
Тому
2) Застосуємо підстановку
звідки
Отже,
3) Застосуємо підстановку
звідки
Представимо підинтегральну функцію у вигляді
Після почленного ділення чисельника дробу на знаменник одержуємо
Зауважимо, що інтеграли виду
є окремим випадком інтегралів (6.3) коли ( Інтеграли (6.5) раціоналізуються підстановкою
Приклад 6.3. Знайти інтеграл
Розв’язання.
Інтеграли виду
Кожен з інтегралів (6.7) – (6.9) можна звести до інтегралу від раціональної функції за допомогою тригонометричних підстановок. Укажемо ці підстановки
І.
ІІ.
ІІІ.
Приклад 6.4. Знайти інтеграли
1)
Розв’язання.
1)
2)
3)
Інтеграли виду
( Даний інтеграл за допомогою підстановки
зводиться до одного з інтегралів виду (6.7) – (6.9).
Дійсно,
Наведемо всі можливі випадки, коли підкорінний вираз існує. 1. Нехай
2.Нехай
3.Нехай
Відповідні приклади рекомендуємо розв’язати самостійно при виконанні завдань п. 7.6 (інтегрування ірраціональних функцій).
ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ
Поиск по сайту: |
 , (6.1)
, (6.1) – натуральні числа;
– натуральні числа; – раціональна функція аргументів
– раціональна функція аргументів  .
. , (6.2)
, (6.2) – найменше спільне кратне знаменників дробів
– найменше спільне кратне знаменників дробів 
 .
.
 ,
, – раціональна функція від
– раціональна функція від  (оскільки
(оскільки  – цілі числа).
– цілі числа). ; 2)
; 2)  ;
; ; 4)
; 4)  .
. і
і  є 6:
є 6: .
.


 .
. .
. є 4. Тому застосуємо підстановку
є 4. Тому застосуємо підстановку  .
. .
.


 .
.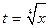

 .
. .
. .
.
 .
. (
(  ):
):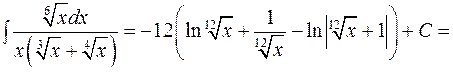
 .
.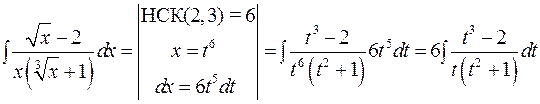 .
. .
. ,
, .
.
 .
. ), одержимо кінцевий результат:
), одержимо кінцевий результат: .
. (6.3)
(6.3) – натуральні числа;
– натуральні числа; , (6.4)
, (6.4) :
: ; 2)
; 2)  ; 3)
; 3)  .
. .
. ;
; ;
;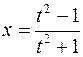 .
. .
. .
.
 .
. ,
, ;
;  .
. .
. .
.
 .
.
 ,
, ,
,  . Тому
. Тому .
. .
.
 , де
, де  .
. (6.5)
(6.5) ).
). (6.6)
(6.6)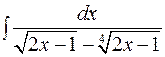 .
.

 .
.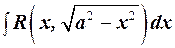 (6.7)
(6.7) (6.8)
(6.8) , (6.9)
, (6.9) – дійсне число.
– дійсне число. або
або  (6.10)
(6.10) або
або  (6.11)
(6.11) або
або  . (6.12)
. (6.12) ; 2)
; 2)  ; 3)
; 3) 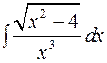 .
.

 .
.




 .
.

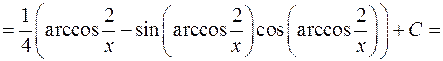
 .
. (6.13)
(6.13) ).
). (6.14)
(6.14) .
. ,
,  .
. .
. .
. .
. ,
, 
 .
.