 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Інтегрування неправильних раціональних дробів
Правило. Для того, щоб про інтегрувати неправильний раціональний дріб
1. Виділити цілу частину з неправильного раціонального дробу (п. 4.1.2). 2. Обчислити
Приклад 4.12. Знайти інтеграл
Розв’язання. Підинтегральна функція – неправильний раціональний дріб (степінь чисельника вищий за степінь знаменника). Виділимо цілу частинну.
Отже,
Перейдемо до інтегрування правильного раціонального дробу
Розкладемо знаменник дробу на множники
Квадратичний множник
При
Таким чином,
Кінцевий результат
5. ІНТЕГРУВАННЯ ДЕЯКИХ
Насамперед зауважимо, що інтеграли від трансцендентних функцій не завжди обчислюються в елементарних функціях. Розглянемо деякі типи інтегралів, які за допомогою певних підстановок можна звести до інтегралів від раціональних функцій (п. 4) або до табличних інтегралів (п. 1).
Раціональна функція двох змінних
Означення. Раціональною функцією двох змінних Приклад 5.1.
Якщо змінні
то функція Приклад 5.2.
Нехай 1) Якщо
2) Якщо
Інтегрування тригонометричних функцій
Розглянемо інтеграл виду
Зауважимо, що підинтегральну функцію, яка раціонально залежить від будь-яких тригонометричних функцій, завжди можна вважати
І. Універсальна тригонометрична підстановка
Інтеграли виду (5.1) завжди зводяться до інтегралів від раціональних функцій (раціоналізуються) за допомогою універсальної тригонометричної підстановки
За відомими тригонометричними формулами
З (5.3) випливає
Тому
де За допомогою універсальної тригонометричної підстановки особливо зручно обчислювати інтеграли виду
Приклад 5.3. Знайти інтеграли
1)
Розв’язання.
1)
2)
3)
Розклад підинтегральної функції на елементарні дроби має вигляд (4.12):
Тому
Невідомі коефіцієнти
Тому
Повертаючись до змінної х, маємо
Звертаємо увагу, що підстановка
ІІ. Інтеграли виду
Для знаходження інтегралів (5.6) рекомендуються наступні заміни
Приклад 5.4. Знайти інтеграли
1)
Розв’язання.
1)
2)
3)
Зокрема, при обчисленні інтегралів виду
(
доцільно застосувати формули
Формули (5.8) та (5.9) дозволяють послідовно знизити степінь тангенса або котангенса.
Приклад 5.5. Знайти інтеграли
1)
Розв’язання.
1)
2)
ІІІ. Інтеграли виду
у випадках
ІІІ.1.
ІІІ.2.
ІІІ.3.
ІІІ.1.
Підинтегральна функція змінює знак при заміні
Рекомендована заміна:
Приклад 5.6. Знайти інтеграли
1)
Розв’язання. 1) Підинтегральна функція містить Зручно спочатку перетворити підинтегральний вираз так, щоб виділити
2) Підинтегральна функція є непарною відносно
3)
Розклад підинтегральної функції на елементарні дроби має вигляд:
Отже,
Тому
ІІІ.2.
Підинтегральна функція змінює знак при заміні Рекомендована заміна:
Приклад 5.7. Знайти інтеграли
1)
Розв’язання.
1. Підинтегральна функція є непарною відносно
2)
ІІІ.3.
Підинтегральна функція не змінюється при заміні знаків у Рекомендована заміна:
Зауважимо, що умова
більш ефективною є підстановка
Для підстановки
випливає, що
Аналогічно для підстановки
Отже, справедливо
Приклад 5.8. Знайти інтеграли
1)
3)
Розв’язання.
1) Підинтегральна функція є парною відносно
Застосуємо підстановку
2) Підинтегральна функція є парною відносно
Застосуємо підстановку
3) Підинтегральна функція є парною відносно
4) Підинтегральна функція не змінюється з одночасної заміни
Отже,
У випадку
Приклад 5.9. Знайти інтеграли
1)
Розв’язання.
2)
IV Інтеграли виду
де Підинтегральна функція має вигляд добутку парних невід’ємних степенів синуса і косинуса. В цьому випадку застосовують формули зниження степеня:
Приклад 5.10. Знайти інтеграли
1)
Розв’язання.
1)
2) Використовуючи тригонометричні формули зниження степеня (5.17) – (5.19), будемо послідовно зводити заданий інтеграл до табличного.
3)
V. Інтеграли виду
де m і n – дійсні числа
Для обчислення інтегралів даного виду використовуються тригонометричні формули:
Приклад 5.11. Знайти інтеграли
1)
Розв’язання. 1) За формулою (5.20)
2) Розглянемо Підинтегральний вираз перетворюється наступним чином:
За формулою (5.20)
За формулою (5.22)
Тому
5.3. Інтеграл виду
Даний інтеграл раціоналізується заміною
де
Приклад 5.12. Знайти інтеграли
1)
Розв’язання.
1)
2)
Таким чином,
Отже,
Поиск по сайту: |
 , треба
, треба як суму інтегралів від цілої раціональної функції (п. 4.3) і правильного раціонального дробу (п 4.4.2).
як суму інтегралів від цілої раціональної функції (п. 4.3) і правильного раціонального дробу (п 4.4.2). .
.


 .
.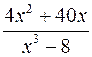 .
. .
. має від’ємний дискримінант. За (4.12)
має від’ємний дискримінант. За (4.12) .
. .
. .
. ;
;  ;
;  .
. .
.



 .
.
 .
. називається функція, що залежить від двох змінних
називається функція, що залежить від двох змінних  і деяких сталих, над якими виконується тільки скінченна кількість чотирьох арифметичних дій: додавання, віднімання, множення і ділення.
і деяких сталих, над якими виконується тільки скінченна кількість чотирьох арифметичних дій: додавання, віднімання, множення і ділення. є раціональною функцією від
є раціональною функцією від  і
і  .
. :
: ,
, є раціональною функцією від
є раціональною функцією від  і
і  .
.
 ,
,  , то
, то .
. ,
,  , то
, то .
. . (5.1)
. (5.1) , оскільки всі тригонометричні функції раціонально виражаються через
, оскільки всі тригонометричні функції раціонально виражаються через  і
і  :
: ,
,  ,
,  ,
, 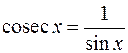 . (5.2)
. (5.2) . (5.3)
. (5.3) ;
;  . (5.4)
. (5.4) , звідки
, звідки  . (5.5)
. (5.5) ,
, – раціональна функція від
– раціональна функція від  .
. .
. ; 2)
; 2)  ; 3)
; 3)  .
.
 .
.
 .
.
 .
. .
. .
. .
. здайдемо за комбінованим методом (п. 4.2.3)
здайдемо за комбінованим методом (п. 4.2.3) .
.


 .
.
 .
. зветься універсальною, оскільки вона завжди раціоналізує інтеграл (5.1). Однак вона часто приводить до надто громіздких обчислень. Тому корисно знати також інші прийоми інтегрування, застосування яких до інтегралів певного виду є ефективним.
зветься універсальною, оскільки вона завжди раціоналізує інтеграл (5.1). Однак вона часто приводить до надто громіздких обчислень. Тому корисно знати також інші прийоми інтегрування, застосування яких до інтегралів певного виду є ефективним. ,
,  ,
,  (5.6)
(5.6) : заміна
: заміна  ;
; : заміна
: заміна  ;
; : заміна
: заміна  .
. ; 2)
; 2)  ; 3)
; 3)  .
.
 .
.

 .
.

 .
. (5.7)
(5.7) – натуральне число)
– натуральне число) , звідки
, звідки  ; (5.8)
; (5.8) , звідки
, звідки 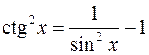 . (5.9)
. (5.9) ; 2)
; 2)  .
.

 .
.
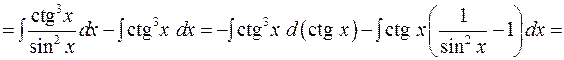

 .
. (5.10)
(5.10)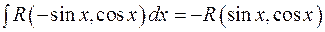 (5.11)
(5.11) (5.12)
(5.12) (5.13)
(5.13) .
. (тобто є непарною відносно
(тобто є непарною відносно  , (
, ( 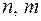 – цілі числа,
– цілі числа, 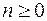 ).
). ; 2)
; 2)  ; 3)
; 3) 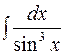 .
. .
. .
.
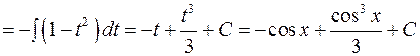 .
. .
.

 .
.
 .
. .
. .
. звідки
звідки  .
. звідки
звідки  .
. ;
;  ;
; ;
; 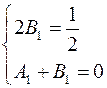 ;
;  .
. .
.

 .
.
 .
. (тобто є непарною відносно
(тобто є непарною відносно  , де (
, де (  – цілі числа
– цілі числа  ; 2)
; 2)  .
.
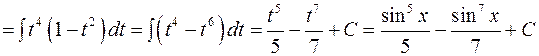 .
.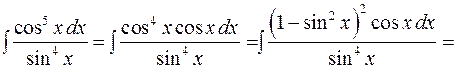

 .
. .
.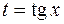 . Зокрема, це відноситься до інтегралів виду
. Зокрема, це відноситься до інтегралів виду і
і  , де
, де  (
(  – ціле).
– ціле). означає: степені чисельника і знаменника є одночасно парними або непарними числами. Для інтегралів
означає: степені чисельника і знаменника є одночасно парними або непарними числами. Для інтегралів .
.
 .
. .
. (5.14)
(5.14) (5.15)
(5.15) ; 2)
; 2)  ;
; ; 4)
; 4)  .
. .
.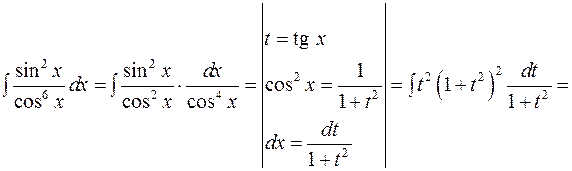
 .
. .
.

 .
.
 .
. ;
; ;
; 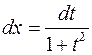
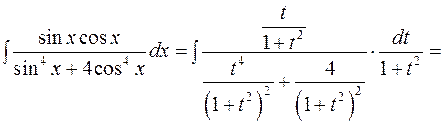
 .
. – парне число для інтегралів виду
– парне число для інтегралів виду  застосовують заміну (5.14), а для інтегралів виду
застосовують заміну (5.14), а для інтегралів виду  застосовують заміну (5.15).
застосовують заміну (5.15). ; 2)
; 2) 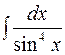 .
.
 .
.
 .
. (5.16)
(5.16) – цілі невід’ємні числа.
– цілі невід’ємні числа. , (5.17)
, (5.17)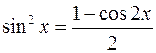 , (5.18)
, (5.18) (5.19)
(5.19) ; 2)
; 2) 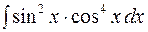 ; 3)
; 3)  .
.

 .
.


 .
.


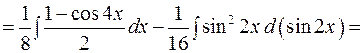

 .
. ,
,  ,
, 
 , (5.20)
, (5.20) , (5.21)
, (5.21) (5.21)
(5.21)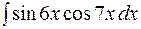 ; 2)
; 2)  .
. .
.
 .
.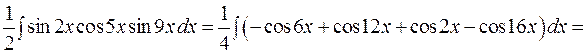
 .
.
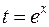 . Дійсно
. Дійсно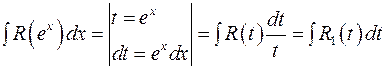 ,
, ; 2)
; 2)  .
. ;
;
 .
. .
. .
. .
.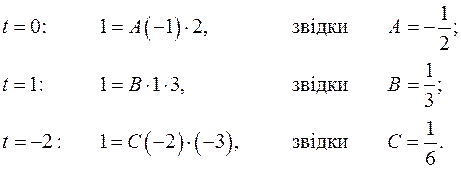
 .
.


 .
.