 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод невизначених коефіцієнтів
Нехай після спрощення обох частин розкладу (4.12) маємо два тотожно рівних многочлени (зліва – з відомими коефіцієнтами, справа – з невідомими коефіцієнтами). З тотожної рівності многочленів випливає, що вони мають рівні степені і рівні між собою коефіцієнти при однакових степенях
Приклад 4.7. розкласти на елементарні дроби правильний раціональний дріб Розв’язання. В прикладі 4.5. було одержано розклад даного дробу методом окремих значень аргументу. Застосуємо метод невизначених коефіцієнтів. Після одержання тотожно рівних многочленів
за результатом алгебраїчних перетворень маємо
Прирівняємо коефіцієнти при однакових степенях
Розв’яжемо одержану системи лінійних рівнянь.
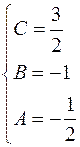
Отже,
Звертаємо увагу, що застосування методу окремих значень аргументу до розв’язання цього прикладу є зручнішим. На практиці часто користуються так званим комбінованим методом, згідно до якого деякі з невідомих коефіцієнтів визначають методом окремих значень аргументу, а інші – методом невизначених коефіцієнтів.
Приклад 4.8. Розкласти на елементарні дроби правильний раціональний дріб
Розв’язання. Цей розклад вже було одержано в прикладі 4.6 методом окремих значень аргументу. Застосуємо для розв’язання цього прикладу комбінований метод. З (4.14)
звідки
В прикладі 4.6 в результаті надання
Для знаходження коефіцієнта
Отже маємо кінцевий результат прикладу (4.6)
Інтегрування цілих раціональних функцій
Інтегрування многочлена
Інтегрування раціональних дробів
Інтегрування елементарних раціональних дробів
Розглянемо інтегрування елементарних раціональних дробів кожного з чотирьох видів (4.10)
І.
ІІ.
ІІІ.
Цей результат одержується за методикою знаходження інтегралу
IV. З методами знаходження
Поиск по сайту: |
 (Твердження 4.2). Прирівнюючи коефіцієнти многочленів при однакових степенях
(Твердження 4.2). Прирівнюючи коефіцієнти многочленів при однакових степенях 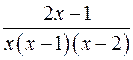 .
.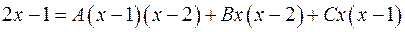
 .
.
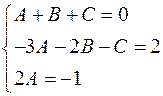 ;
;  ;
;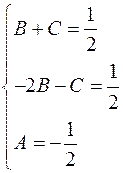 ;
; 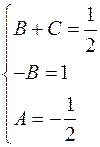 ;
; 
 .
. .
.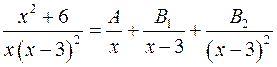 ,
,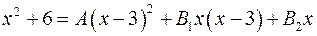 . (4.15)
. (4.15)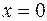 і
і  ) було одержано
) було одержано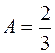 ;
; 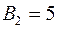 .
.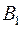 прирівняємо в (4.15) коефіцієнти при
прирівняємо в (4.15) коефіцієнти при 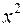 в лівій і правій частинах.
в лівій і правій частинах.
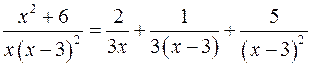 .
. (4.1) утруднень не викликає. Воно зводиться до інтегрування алгебраїчної суми степеневих функцій (табличний інтеграл 2, п 1.2).
(4.1) утруднень не викликає. Воно зводиться до інтегрування алгебраїчної суми степеневих функцій (табличний інтеграл 2, п 1.2).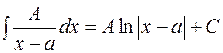 (табличний інтеграл 3, п. 1.2).
(табличний інтеграл 3, п. 1.2).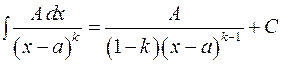 (табличний інтеграл 2, п. 1.2).
(табличний інтеграл 2, п. 1.2).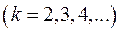
 .
.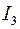 (п. 3.3).
(п. 3.3).