 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Перший тип заміни змінної
Функція незалежної змінної
властивість інваріантності формул інтегру- вання (2.1)
Застосуємо заміну змінної до розв’язання прикладу 2.5. Приклад 2.6. Знайти інтеграли:
1)
4)
Розв’язання. 1)
2)
3)
4)
5)
6)
Звертаємо увагу, що в прикладах 5) і 6) перетворення підинтегрального виразу
не здійснювалось. Відповідну заміну змінної Підкреслимо, що загального «рецепту» вибору тієї чи іншої заміни не існує. Однак, слід мати на увазі наступну рекомендацію: якщо в підінтегральному виразі є готовий диференціал функції
Приклад 2.7. Знайти інтеграли:
1)
3)
5)
Розв’язання.
1)
2)
3)
4)
5)
В цьому прикладі після почленного ділення чисельника дробу підинтегральної функції на знаменник заданий інтеграл зведено до суми двох інтегралів: Перший інтеграл знаходяться безпосередньо:
Другий інтеграл береться заміною змінної:
Отже, заданий інтеграл
6)
В даному прикладі для досягнення результату довелося зробити заміну змінної двічі. Перша заміна дозволила спростити заданий інтеграл, а друга заміна звела проміжковий інтеграл
Зауваження. З формул (2.1) і (2.2) випливає справедливість рівності
де
Отже формула (2.9) є основою другого типа заміни змінної – підстановки.
Другий тип заміни змінної (підстановка)
Незалежна змінна заміняється функцією нової змінної
де Розглянемо у загальному вигляді умови застосування другого типу заміни змінної і наведемо приклади.
інтеграл формула складний для (2.9) відома первісна безпосереднього інтегрування
Приклад 2.8. Знайти інтеграли
1)
4)
Розв’язання.
1) Розглянемо
2)
3) Розглянемо
Функція
4)
5) Розглянемо
Зауважимо, що коли
6)
Таким чином, на практиці застосують перший і другий типи заміни змінної. Заміну змінної підбирають так, щоб в результаті перетворень інтеграли були табличними або зводилися до відомих інтегралів. Після застосування методу заміни змінної завжди необхідно повернутися до заданої змінної інтегрування.
Поиск по сайту: |
 заміняється новою змінною:
заміняється новою змінною: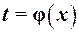 .
.
 .
.
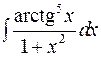 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
. до вигляду
до вигляду
 було спробувано в передбаченні, що таке представлення є можливим. В ітозі вдалося одержати вірні результати інтегрування.
було спробувано в передбаченні, що таке представлення є можливим. В ітозі вдалося одержати вірні результати інтегрування. (тобто
(тобто  ), або вираз, що відрізняється від
), або вираз, що відрізняється від  .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ; 6)
; 6)  .
.
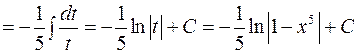 .
.
 .
.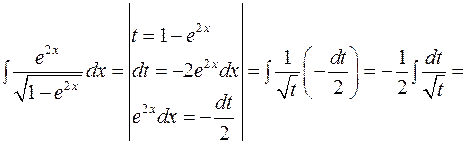
 .
.
 .
.
 .
. та
та  .
.
 .
.
 .
.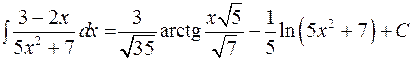 .
.
 .
. до табличного інтегралу:
до табличного інтегралу:  .
. , (2.8)
, (2.8) і
і  в формулі (2.8), одержимо:
в формулі (2.8), одержимо: . (2.9)
. (2.9) ,
,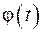 має обернену функцію
має обернену функцію  .
.


 для функції
для функції 
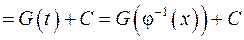 .
.
 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5) 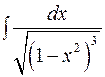 ; 6)
; 6) 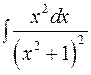 .
.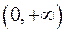 . Щоб позбутися ірраціональності у знаменнику підинтегральної функції, виконаємо підстановку:
. Щоб позбутися ірраціональності у знаменнику підинтегральної функції, виконаємо підстановку: . Функція
. Функція 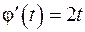 в своєї області визначення і має обернену функцію
в своєї області визначення і має обернену функцію  . Отже,
. Отже,

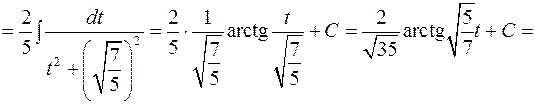
 .
.

 .
. (
( 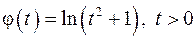 ).
). в своєї області визначення і обернену функцію
в своєї області визначення і обернену функцію  . Маємо
. Маємо


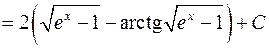 .
.


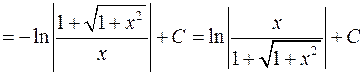 .
. . Дійсно,
. Дійсно,  . Щоб позбутися ірраціональності в знаменнику підинтегральної функції в результаті застосування основної тригонометричної тотожності, виконаємо підстановку:
. Щоб позбутися ірраціональності в знаменнику підинтегральної функції в результаті застосування основної тригонометричної тотожності, виконаємо підстановку:  .
.  є неперервною функцією в області визначення
є неперервною функцією в області визначення  має обернену функцію
має обернену функцію 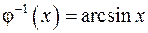 ,
, 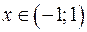 . Отже
. Отже
 .
. . Тому при розв’язанні прикладу правомірний наступний перехід:
. Тому при розв’язанні прикладу правомірний наступний перехід:  .
.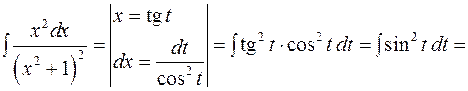

 .
.