 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод інтегрування частинами. 2.3.1. Формула інтегрування частинами, її зміст та рекомендації щодо застосування.
2.3.1. Формула інтегрування частинами, Метод інтегрування частинами ґрунтується на використанні формули диференціала добутку двох функцій:
звідки випливає рівність
Інтегруючи обидві частини останньої рівності, одержимо
або
Оскільки до складу невизначеного інтеграла
Зміст цієї формули полягає у тому, що при обчисленні невизначеного інтегралу
Після цього обчислення інтегралу 1) при обчисленні
2) при обчисленні інтегралу в правій частині формули (2.10):
Замість одного складного інтегрування виконуються два, більш простих. Таким чином, інтегрування виконується частинами.
Приклад 2.9. Знайти інтеграл Розв’язання. Представимо підинтегральний вираз
Зауважимо, що в результаті останнього інтегрування достатньо знайти один множник Маємо
формула інтегрування частинами (2.10)
Звертаємо увагу на те, що при інтегруванні частинами треба намагатися, щоб інтеграл справа в формулі (2.10) був простішим, ніж інтеграл зліва. В розглянутому прикладі, якщо зробити вибір множників
Взагалі метод інтегрування частинами має більш обмежену область застосування, ніж метод заміни змінної. Але існують класи інтегралів, які обчислюються саме методом інтегрування частинами. Укажемо ці класи і надамо рекомендації щодо розбиття підинтегрального виразу на множники
Таблиця 1 – Деякі рекомендації щодо вибору множників u і dv в методі інтегрування частинами
Приклад 2.9. Знайти інтеграли.
1)
3)
При знаходженні всіх інтегралів даного прикладу будемо дотримуватися рекомендацій п. І таблиці 1, відповідно до яких за
Розв’язання.
1) формула (2.10)
2) формула (2.10)
3) формула (2.10)
4) формула (2.10)
При знаходженні інтегралів наступного прикладу будемо дотримуватись рекомендацій п. ІІ таблиці. За множник
Приклад 2.10. Знайти інтеграли.
1)
3)
Розв’язання.
1)
2)
3)
4)
2.3.2. Двократне застосування формули
Іноді для знаходження інтегралів формулу інтегрування частинами (2.10) доводиться застосовувати кілька разів. Розглянемо приклад щодо двократного застосування цієї формули.
Приклад 2.11.Знайти інтеграли.
1)
3)
Розв’язання.
1) Клас І (табл. 1)
Клас І (табл. 1)
2) Клас ІІ (табл. 1)
Клас ІІ (табл. 1)
3) Клас ІІ (табл. 1)
4)
В результаті двократного інтегрування частинами в правій частині рівності одержано шуканий інтеграл
Зауваження. Пояснимо появу сталого множника С в рівності (**). Справа в тому, що кожний з інтегралів І в лівій і правій частині рівності (*) являє собою вираз
де 2.3.3. Застосування методу інтегрування частинами
Приклад 2.12. Знайти інтеграли.
1)
3)
Розв’язання.
1)
2)
3)
4)
Знайдемо
Отже,
3. ІНТЕГРУВАННЯ ДЕЯКИХ ВИРАЗІВ,
На практиці часто зустрічаються інтеграли, що містять квадратний тричлен у знаменнику підинтегрального виразу, а саме
Наведемо алгоритми знаходження кожного з цих інтегралів і розглянемо відповідні приклади.
Знаходження інтегралу
Цей інтеграл знаходиться шляхом виділення повного квадрату з квадратного тричлену
Дійсно, перетворимо квадратний тричлен у знаменнику так, щоб він уявляв собою суму або різницю квадратів:
Позначимо
Тоді
Одержано табличні інтеграли:
або
Приклад 3.1.Знайти інтеграли
1)
3)
Розв’язання.
1)
2)
3)
4)
Знаходження інтегралу
Аналогічно п. 3.1. перетворимо підкорінний вираз в знаменнику підинтегральної функції так, щоб він уявляв собою суму або різницю квадратів.
Тоді а) якщо Отже,
б) якщо Отже,
Приклад 3.2.Знайти інтеграли
1) Розв’язання.
1)
2)
Знаходження інтегралу
Цей інтеграл знаходиться шляхом виділення в чисельнику Дійсно перетворимо підинтегральний вираз в інтегралі
Знайдемо
Отже,
Приклад 3.3. Знайти інтеграли.
1)
3)
Розв’язання.
1)
Знайдемо перший доданок суми:
Знайдемо другий доданок суми:
Отже, даний інтеграл
2)
Знайдемо перший доданок суми:
Знайдемо другий доданок суми:
Отже, даний інтеграл
3)
4)
Знаходження інтегралу
Аналогічно п 3.3 для знаходження інтегралу застосують прийом виділення в чисельнику підинтегрального виразу похідної знаменника. Після зазначеного перетворення інтеграл Дійсно, перетворимо підинтегральний вираз в інтегралі
Знайдемо
Отже,
Приклад 3.4. Знайти інтеграли:
1)
Розв’язання.
1)
Знайдемо
Знайдемо
Таким чином, даний інтеграл
2)
Поиск по сайту: |
 ,
, .
.
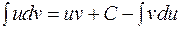 .
. вже входить довільна стала, то до неї можна приєднати і доданок С. Отже, одержуємо формулу інтегруванні частинами:
вже входить довільна стала, то до неї можна приєднати і доданок С. Отже, одержуємо формулу інтегруванні частинами: . (2.10)
. (2.10) підинтегральний вираз
підинтегральний вираз  деяким чином представляється у вигляді добутку двох множників:
деяким чином представляється у вигляді добутку двох множників:  і
і  , тобто
, тобто .
. із виразу
із виразу  ;
;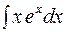 .
.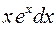 у вигляді добутку двох множників х і
у вигляді добутку двох множників х і  . Нехай
. Нехай  і
і  . Продиференціюємо множник
. Продиференціюємо множник  і проінтегруємо множник
і проінтегруємо множник  .
. .
.






 .
.



 .
.
 – многочлен;
– многочлен;
 – дійсне число
– дійсне число 

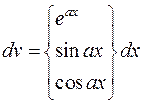
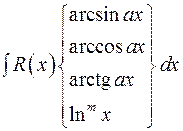
 – алгебраїчна функція;
– алгебраїчна функція;
 ;
;
 – натуральне число
– натуральне число



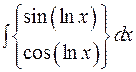


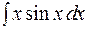 ; 2)
; 2)  ;
;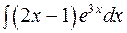 ; 4)
; 4)  .
.

 .
.
 .
.
 .
.

 .
. ,
,  ,
, 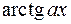 або
або  , яка спрощується при диференціюванні.
, яка спрощується при диференціюванні.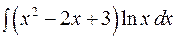 ; 2)
; 2)  ;
; ; 4)
; 4)  .
.
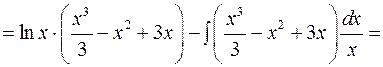

 .
.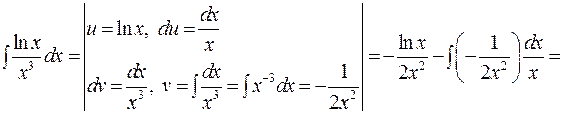
 .
.
 .
.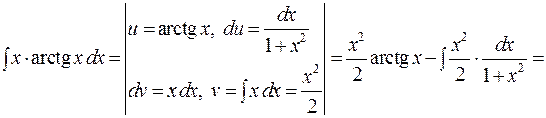
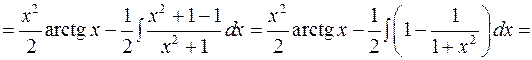

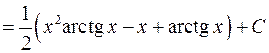 .
. ; 2)
; 2)  ;
; ; 4)
; 4)  .
.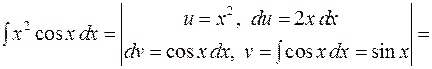
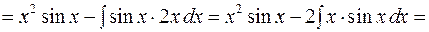

 .
.

 .
.

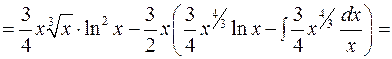
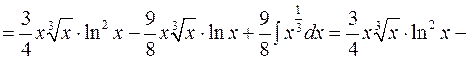
 .
.



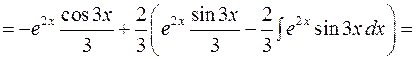

 .
. . Позначимо цей інтеграл І. Отже, одержано лінійне рівняння відносно шуканого інтегралу І:
. Позначимо цей інтеграл І. Отже, одержано лінійне рівняння відносно шуканого інтегралу І: . (*)
. (*) . (**)
. (**) .
. .
. .
.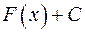 ,
, – яка-небудь первісна для
– яка-небудь первісна для  , а С – довільна стала, яка може обиратися для цих інтегралів по різному. Тому інтеграл І в лівій і правій частині рівності (*) можуть відрізнятися на сталу.
, а С – довільна стала, яка може обиратися для цих інтегралів по різному. Тому інтеграл І в лівій і правій частині рівності (*) можуть відрізнятися на сталу.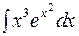 ; 2)
; 2)  ;
; ; 4)
; 4) 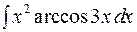 .
.

 .
.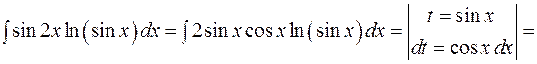


 .
.



 .
.
 .
. методом заміни змінної.
методом заміни змінної.

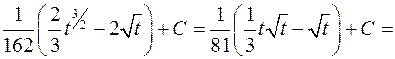
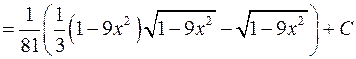 .
. .
.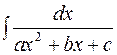 ;
;  ;
; ;
;  .
. (3.1)
(3.1) , що міститься в знаменнику підинтегрального виразу. В результаті одержується табличний інтеграл виду
, що міститься в знаменнику підинтегрального виразу. В результаті одержується табличний інтеграл виду або
або  .
.
 .
.
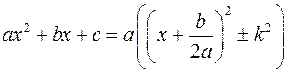 .
.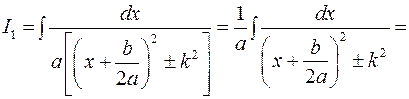
 .
.
 .
. ; 2)
; 2)  ;
; ; 4)
; 4) 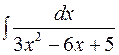 .
.

 .
.
 .
.

 .
.
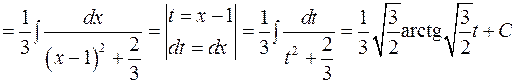
 .
. (3.2)
(3.2) .
. , оскільки
, оскільки  , то
, то  .
. ;
; , оскільки
, оскільки  , то
, то  , де
, де  .
. .
. ; 2)
; 2)  .
.
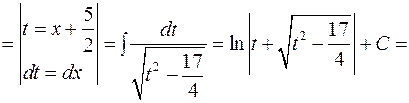
 .
. .
.


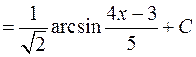 .
. (3.3)
(3.3) підинтегрального виразу похідної
підинтегрального виразу похідної  знаменника
знаменника  . Після зазначеного перетворення інтеграл
. Після зазначеного перетворення інтеграл 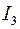 представляється у вигляді суми двох інтегралів, один з яких є інтегралом
представляється у вигляді суми двох інтегралів, один з яких є інтегралом  .
.
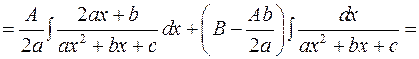
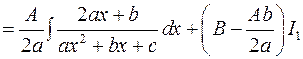 .
.
 .
. .
. ; 2)
; 2)  ;
;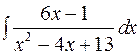 ; 4)
; 4)  .
.
 .
.
 .
.
 .
. .
.
 .
.
 .
.

 .
. .
.




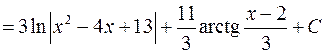 .
.




 .
. (3.4)
(3.4) представляється у вигляді суми двох інтегралів, один з яких є інтегралом
представляється у вигляді суми двох інтегралів, один з яких є інтегралом  .
.

 .
.
 .
. .
. ; 2)
; 2)  .
.
 .
.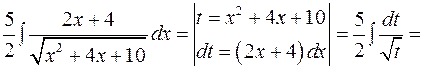
 .
.

 .
. .
.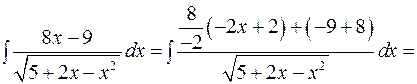




 .
.