 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Как вычислить длину дуги кривой?
Помимо нахождения площади и объёма тела вращения, вездесущий определённый интеграл позволяет рассчитать и другие показатели, в частности длину дуги кривой. Пусть некоторая функция
Согласно геометрическому смыслу, длина не может быть отрицательной, и это заведомо гарантируется неотрицательностью подынтегральной функции Другой хорошей новостью является тот факт, что в практических примерах, как правило,не нужно строить чертежа. Это была единственная иллюстрация в статье, чтобы вы быстрее поняли, о чём вообще идёт речь. Впрочем, начнём с кривой, которую всем вбили в голову ещё в далёком детстве =) Пример 1 Вычислить длину дуги параболы Решение: принимая во внимание «иксовые» координаты точек, определяем пределы интегрирования
А вот и первый камень преткновения. Интеграл данного вида детально разобран в Примере №5 урока Сложные интегралы, он интегрируется по частям и сводится к себе. Сначала удобно найти первообразную:
Интегрируем по частям:
Открываем одиночной «звёздочкой» основное решение и используем формулу Ньютона-Лейбница:
Ответ: Скрупулёзно не проверял, но если взглянуть на параболу, то очень и очень похоже на правду. Громоздких и страшных результатов бояться не нужно, рАвно, как и длинных решений! Следующие разминочные задачи для самостоятельного решения Пример 2 Вычислить длину дуги полукубической параболы Интеграл здесь будет значительно проще, чем в предыдущем примере. Однако за кажущейся простотой нередко скрывается коварство. Так, вроде бы похожее условие «Вычислить длину дуги полукубической параболы Да, в рассматриваемом типе задач обычно не требуется выполнять чертёж, но всегдаполезно, а иногда и очень важнознать, что это за линия и КАК выглядит ей график ;-) Пример 3 Вычислить длину дуги кривой Это более распространённый вариант формулировки – когда промежуток интегрирования указан в виде двойного неравенства. А что тут смущает? Люди без комплексов давно интегрируют по любой переменной, и я ещё в статье Объем тела вращения предлагал вам расширить свои взгляды =) Обратная функция Кстати, в первом примере можно рассмотреть правую ветвь параболы В следующем параграфе рассмотрим критически важную вещь, касающуюся всех задач урока:
Поиск по сайту: |
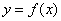 , либо параметрически
, либо параметрически 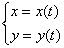 , или же уравнением
, или же уравнением 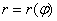 в полярной системе координат. Для каждого случая будут разобраны практические примеры с подробными комментариями о типичных особенностях решения этой задачи. Более того, по ходу изложения материала вас ждёт специальное предложение, которое должно понравиться ;-)
в полярной системе координат. Для каждого случая будут разобраны практические примеры с подробными комментариями о типичных особенностях решения этой задачи. Более того, по ходу изложения материала вас ждёт специальное предложение, которое должно понравиться ;-)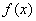 непрерывна на отрезке
непрерывна на отрезке 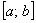 , и её график на данном промежутке представляет собой кривую или, что то же самое, дугу кривой
, и её график на данном промежутке представляет собой кривую или, что то же самое, дугу кривой 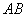 :
:
 на
на  или компактнее:
или компактнее: 
 (при разумеющемся условии
(при разумеющемся условии  ). Таким образом, в данной задаче не возникает дополнительных хлопот по поводу того, как и где «петляет» график (выше оси, ниже оси и т.д.).
). Таким образом, в данной задаче не возникает дополнительных хлопот по поводу того, как и где «петляет» график (выше оси, ниже оси и т.д.). от точки
от точки  до точки
до точки 
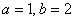 и используем формулу:
и используем формулу: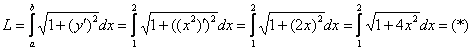



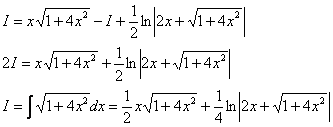


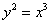 от точки
от точки  до точки
до точки 
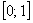 » далеко не эквивалентно и приводит к совершенно другому ответу.
» далеко не эквивалентно и приводит к совершенно другому ответу. ,
, 
 и её производная
и её производная  непрерывны на отрезке
непрерывны на отрезке  , поэтому применима зеркальная формула
, поэтому применима зеркальная формула  , где
, где  и
и 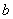 , естественно, уже «игрековые» пределы интегрирования.
, естественно, уже «игрековые» пределы интегрирования.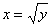 с пределами интегрирования
с пределами интегрирования  , правда, хрен редьки не слаще. Хотя любители оценят, интеграл получается трудный, но вполне реалистичный.
, правда, хрен редьки не слаще. Хотя любители оценят, интеграл получается трудный, но вполне реалистичный.