 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Как построить фигуру, если её НАДО построить, но под рукой нет программы?
Не унываем, схематический чертёж отнимет не так уж много времени. Такой версии, скорее всего, будет достаточно, ведь это не главная часть задания. В который раз взглянем на график косинуса: на интервале Так же очевидно, что при Давайте найдём дополнительную опорную точку. Напрашивается угол в 45 градусов: В силу симметрии линии: Как называется эта фигура, я не знаю, …сейчас немного проанализировал, …какая-тоалгебраическая кривая 6-го порядка: Ну и, конечно же, не забываем по клеточкам оценить, что полученное значение площади Пример 2 Вычислить площадь фигуры, ограниченной линией Это пример для самостоятельного решения. Примерный образец чистового оформления задачи в конце урока. Если на пути встаёт область определения, то блицкриг тоже вполне осуществим: Пример 3 Вычислить площадь фигуры, ограниченной линией Решение: данное уравнение задаёт двухлепестковую полярную розу, область определения:
(*) На данном шаге использовали чётность подынтегральной функциина симметричном относительно нуля отрезке интегрирования. С геометрической точки зрения это означает, что лепесток розы симметричен относительно своей центральной оси. В предыдущих двух примерах фигуры тоже были симметричными, но, как ни странно, в рассматриваемом типе задач излишнее обмусоливание данного факта зачастую только удлиняет решение. Ответ: Если считать, что уравнение Следующие короткие задачи предназначены для самостоятельного решения: Пример 4 Вычислить площадь фигуры, ограниченной линией, заданной уравнением Пример 5 Вычислить площадь фигуры, ограниченной линией, заданной уравнением Кривая 4-го примера называется лемнискатой Бернулли, в 5-ом примере данатрёхлепесковая роза. Напоминаю, что если есть возможность быстро построить чертеж, то его лучше построить. А здесь они, к слову, быстро строятся и вручную. После интенсивной разминки на опушке надеваем хоккейную маску и с воодушевлением углубляемся в лес за новыми жертвами: Пример 6 Вычислить площадь фигуры, ограниченной линиями Решение: в условии даны две линии, и здесь хоть о чертеже и молчок, но без него уже трудно. Какую кривую задаёт уравнение Уравнение же 1) Вычислим площадь круга. Пределы интегрирования
Результат, не забываем, легко проверяется с помощью школьной формулы. 2) Вычислим площадь лепестка розы, расположенного в пределах
3) Площадь искомой фигуры:
Ответ: В рассмотренном примере фигурировали разные отрезки интегрирования, и площадь выразилась разностью
Нетрудно уловить, что общий мотив похож на вычисление площади в прямоугольных координатах по формуле Следующий баян лучше не пропускать: Пример 7 Вычислить площадь фигуры, ограниченной линиями Краткое решение с чертёжом в конце урока. И в заключение ещё одна распространённая разновидность задачи, после чего будет специальное предложение для самых увлечённых маньяков: Пример 8 Вычислить площадь фигуры, ограниченной линиями, заданными в полярных координатах Решение: с художеством особых проблем не возникает, однако фигура, ограниченная окружностями Сначала разберёмся, как найти луч Сбрасываем косинус на нижний ярус левой части и превращаем дробь в тангенс: Таким образом: Из чертежа следует, что площадь фигуры нужно искать как сумму площадей: 1) На промежутке
2) На промежутке
Интегралы настоятельно рекомендую считать РАЗДЕЛЬНО – риск допустить ошибку по невнимательности как никогда велик. Только что ещё раз убедился на собственном опыте, пытаясь оформить решение «одной строкой». 3) А вот теперь пользуемся аддитивностью площади: Ответ: Аналогичное задание для самостоятельного решения: Пример 9 Вычислить площадь фигуры, ограниченной линиями, заданными в полярных координатах Заметьте, что условие данной задачи требует выполнения чертёжа (даже если Вы с ходу представили, как выглядит фигура и даже если мысленно всё рассчитали). Всегда обращайте внимание на формулировку. Примерный образец решения совсем близко. Надо сказать, что я разобрал не самые сложные задания, дабы не отпугнуть «чайников». Желающие могут ознакомиться с дополнительными прорешанными примерами из сборника Кузнецова (задача №16). Но всё-таки приберегите немного сил на вычисление площадей фигур, ограниченных параметрически заданными линиями=) И удачи вам в пятницу 13-го! Решения и ответы: Пример 2:Решение: найдём область определения: Ответ: Пример 4:Решение: область определения: Пример 5:Решение: данное уравнение задаёт трёхлепестковую розу, область определения: Пример 7:Решение: выполним чертёж: Пример 9:Решение: найдём угловое направление пересечения окружностей: Автор: Емелин Александр
Высшая математика для заочников и не только >>> (Переход на главную страницу) Как можно отблагодарить автора?
На занятиях Вычисление площади с помощью определённого интеграла и Объем тела вращения мы рассмотрели два самых важных приложения определённого интеграла, в которых демонстрационная криволинейная трапеция ограничена осью абсцисс, отрезками прямых Встречайте старую знакомую: Рассмотрим ситуацию, когда эта же функция задана в параметрическом виде
Поиск по сайту: |
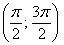 косинус принимает такие же по модулю значения, что и на интервале
косинус принимает такие же по модулю значения, что и на интервале 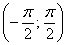 , только со знаком «минус». Поскольку у нас косинус возводится в квадрат, то фигура, ограниченная графиком функции
, только со знаком «минус». Поскольку у нас косинус возводится в квадрат, то фигура, ограниченная графиком функции 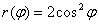 , будет состоять из двух одинаковых и симметричных относительно полюса частей, вершины которых, очевидно, находятся в следующих точках:
, будет состоять из двух одинаковых и симметричных относительно полюса частей, вершины которых, очевидно, находятся в следующих точках: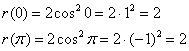
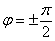 полярный радиус равен нулю.
полярный радиус равен нулю.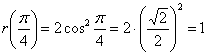

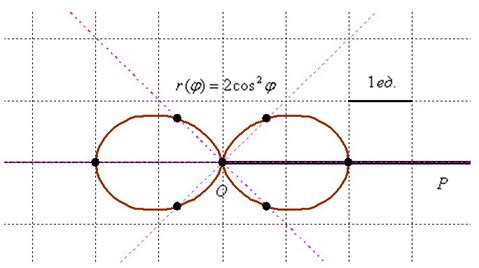
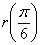 для более точного построения чертежа.
для более точного построения чертежа.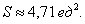 похоже на правду.
похоже на правду.
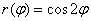
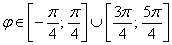 . Лепестки одинаковы, поэтому достаточно найти площадь одного из них, а результат удвоить. Удваивать рекомендую сразу же (в конце задания забывается просто «на ура»):
. Лепестки одинаковы, поэтому достаточно найти площадь одного из них, а результат удвоить. Удваивать рекомендую сразу же (в конце задания забывается просто «на ура»):
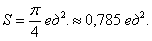
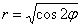 в полярной системе координат.
в полярной системе координат.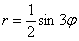 в полярной системе координат.
в полярной системе координат.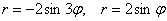 .
.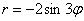 ? В статье о полярных координатах мы подробно разбирали и строили график полярной розы
? В статье о полярных координатах мы подробно разбирали и строили график полярной розы 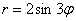 с лепестками на промежутках
с лепестками на промежутках  . Знак «минус» всё перевернёт с ног на голову (а если академичнее – отобразит симметрично относительно полярной оси и её продолжения) и лепестки розы
. Знак «минус» всё перевернёт с ног на голову (а если академичнее – отобразит симметрично относительно полярной оси и её продолжения) и лепестки розы  расположатся в секторах
расположатся в секторах 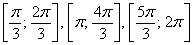 .
.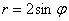 значительно проще, оно определяет типовую окружность:
значительно проще, оно определяет типовую окружность: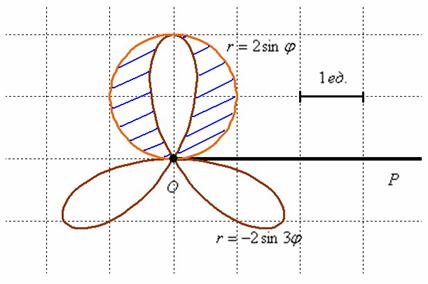
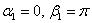 , по формуле:
, по формуле:
 :
:
 … математический каламбур прямо какой-то =)
… математический каламбур прямо какой-то =)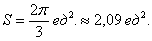 , что весьма правдоподобно
, что весьма правдоподобно . Однако на практике данные промежутки чаще совпадают и по причине линейности интеграла формула упрощается. Сформулирую правило в общем виде: если функции
. Однако на практике данные промежутки чаще совпадают и по причине линейности интеграла формула упрощается. Сформулирую правило в общем виде: если функции  непрерывны и неотрицательны на некотором отрезке
непрерывны и неотрицательны на некотором отрезке 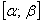 , и при этом
, и при этом 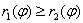 , то площадь фигуры, ограниченной отрезками лучей
, то площадь фигуры, ограниченной отрезками лучей 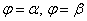 и данными линиями, равна:
и данными линиями, равна:
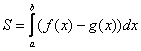 , где из «верхней» функции, вычитается «нижняя».
, где из «верхней» функции, вычитается «нижняя».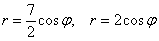 .
. .
. , не определена однозначно и поэтому в условии наложено дополнительное ограничение на угол
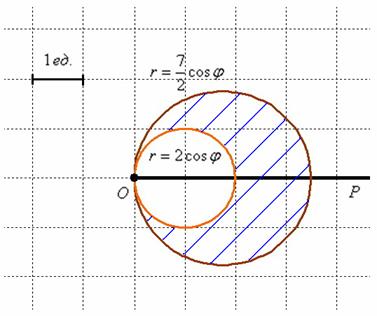
, не определена однозначно и поэтому в условии наложено дополнительное ограничение на угол 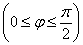 , из которого следует, что необходимо вычислить заштрихованную площадь:
, из которого следует, что необходимо вычислить заштрихованную площадь:
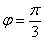 , по которому пересекаются окружности. Очень просто – приравниваем функции и решаем уравнение:
, по которому пересекаются окружности. Очень просто – приравниваем функции и решаем уравнение: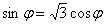
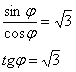
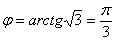
 фигура ограничена отрезком луча
фигура ограничена отрезком луча  (синяя штриховка).
(синяя штриховка).
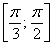 фигура ограничена тем же отрезком луча
фигура ограничена тем же отрезком луча  (зелёная штриховка).
(зелёная штриховка).
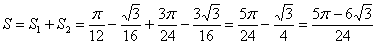
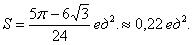
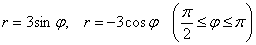 . Выполнить чертёж.
. Выполнить чертёж.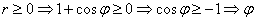 – любое.
– любое. , в данном случае
, в данном случае 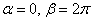 :
: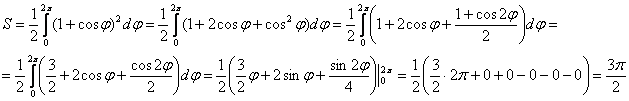
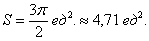
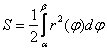 , вычислим площадь на отрезке
, вычислим площадь на отрезке  , результат удвоим:
, результат удвоим:
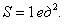
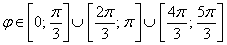


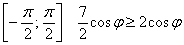 , таким образом:
, таким образом:
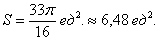
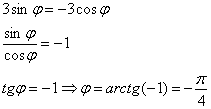
 , поэтому рассматриваем противоположнонаправленный луч
, поэтому рассматриваем противоположнонаправленный луч 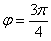 . Выполним чертёж:
. Выполним чертёж: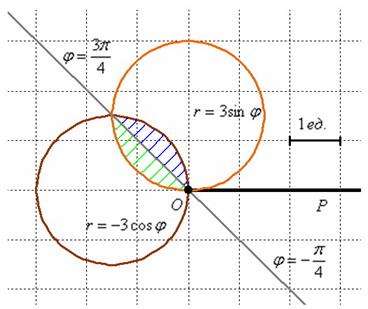
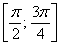 фигура ограничена отрезком луча
фигура ограничена отрезком луча  .
.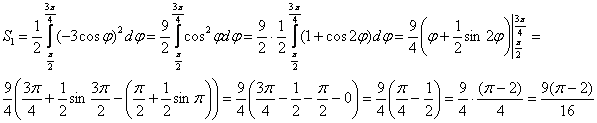
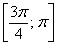 фигура ограничена отрезком луча
фигура ограничена отрезком луча  .
.
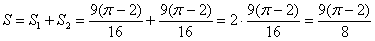
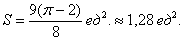
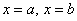 и графиком функции
и графиком функции 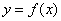 , которая непрерывна и не меняет знак на отрезке «а-бэ». Но в некоторых практических заданиях функция может быть задана в параметрическом виде
, которая непрерывна и не меняет знак на отрезке «а-бэ». Но в некоторых практических заданиях функция может быть задана в параметрическом виде 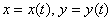 , и наша сегодняшняя задача – научиться считать площадь и объем, если вышла такая незадача =) Понятие параметрической формы я достаточно подробно раскрыл в статье о производной параметрически заданной функции, и в курсе аналитической геометрии на уроках об уравнении прямой на плоскости и уравнениях прямой в пространстве.
, и наша сегодняшняя задача – научиться считать площадь и объем, если вышла такая незадача =) Понятие параметрической формы я достаточно подробно раскрыл в статье о производной параметрически заданной функции, и в курсе аналитической геометрии на уроках об уравнении прямой на плоскости и уравнениях прямой в пространстве.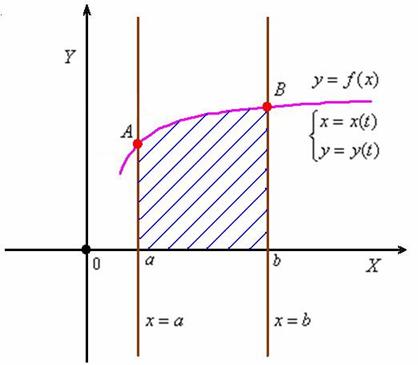
 или, если короче:
или, если короче: 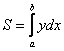 .
.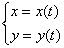 .
.