|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Общая концепция задачи интегрирования
В предыдущих пунктах мы разобрали задачу нахождения площади, но это частная и довольно малая область применения интегрального исчисления. Существует великое множество задач интегрирования, при этом наибольшим разнообразием отличается даже не математика, а физика. Вернёмся к самому смыслу термина: интегрирование – это объединение. А объединить, как вы понимаете, можно много чего =) И в общем виде задача интегрирования ставится следующим образом, не судите строго, формулирую своими словами: Требуется найти значение величины В предположении о непрерывности функции Сначала рассматривается бесконечно малый отрезок Далее проводится объединение (интегрирование) всех бесконечно малых элементов Примечание: в теории и практике вышеизложенные равенства почти всегда записывают в обратном порядке: Давайте вспомним 1-ый чертёж урока, где мы установили, что площадь Объединяя (интегрируя) эти бесконечно малые прямоугольники по отрезку Заключительные примеры позволят вам ещё лучше понять сущность интегрирования: Пример 2 Вычислить объём эллипсоида Решение: перепишем уравнение эллипсоида в каноническом виде
Прежде всего, обратим внимание на заштрихованную «площадку» Теперь поднимаем заштрихованную «площадку» ладошкой вверх – полуоси В чём состоит трудность нахождения объёма На первом шаге рассматриваем «площадку» На втором шаге «плавно поднимаемся на лифте с 0-го на 5-ый этаж», объединяя ВСЕ элементарные слои Суть разобрана, остальное – дело техники: 1) Найдём функцию
Поскольку дело происходит в 1-ом октанте, то перед корнем будет знак «плюс»: 2) Аналогично находим функцию длины малой полуоси. В уравнении эллипсоида
3) Составим функцию площади
И, наконец, «запускаем лифт», объединяя элементарные частички объёма Так как рассматривалась только Ответ: Если решить задачу с каноническим уравнением Следует отметить, что в общем случае эллипсоид не является телом вращения, поэтому к нему не применим «обычный» метод нахождения объема, изложенный в статье Объем тела вращения. Таким образом, разобранная задача оказывается не только поучительной, но ещё и крайне полезной. Желающие могут найти здесь ещё порядка 30-ти похожих примеров и потренироваться. Для полноценной картины как нельзя кстати будет физика: Пример 3 Найти путь, пройдённый телом в промежуток времени от Решение: обозначим через Немного проанализируем задачу. Вот если бы тело двигалось с постоянной скоростью, например, 7 м/с, то никаких проблем – оно бы за 3 секунды прошло путь в Как быть? На помощь приходит интегрирование. Рассмотрим бесконечно малый промежуток времени Всё что осталось сделать – это объединить микроскопические «шажочки»
Ответ: 45 метров Ну а у меня такое впечатление, что эту статью я создавал 45 лет =) …хотя вроде бы она не самая большая, да и чертежи быстро сделал… Наверное по той причине, что довольно долго обдумывал, что включить в содержание, а что оставить за кадром. Так или иначе, думаю, что отобранная информация значительно повысила ваш уровень понимания темы. Желаю успехов! Автор: Емелин Александр
Высшая математика для заочников и не только >>> (Переход на главную страницу) Как можно отблагодарить автора?
Как вычислить объем тела вращения
Помимо нахождения площади плоской фигуры с помощью определенного интегралаважнейшим приложением темы является вычисление объема тела вращения. Материал простой, но читатель должен быть подготовленным: необходимо уметь решатьнеопределенные интегралы средней сложности и применять формулу Ньютона-Лейбница в определенном интеграле. Как и для задачи нахождения площади, нужны уверенные навыки построения чертежей – это чуть ли не самое важное (поскольку интегралы сами по себе чаще будут лёгкими). Освоить грамотную и быструю технику построения графиков можно с помощью методических материалов Графики и свойства Элементарных функций и Геометрические преобразования графиков. Но, собственно, о важности чертежей я уже неоднократно говорил на уроке Определенный интеграл. Как вычислить площадь фигуры. Вообще в интегральном исчислении очень много интересных приложений, с помощью определенного интеграла можно вычислить площадь фигуры, объем тела вращения, длину дуги, площадь поверхности вращения и многое другое. Поэтому будет весело, пожалуйста, настройтесь на оптимистичный лад! Представьте некоторую плоскую фигуру на координатной плоскости. Представили? ... Интересно, кто что представил… =))) Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать, причем вращать двумя способами: – вокруг оси абсцисс В данной статье будут разобраны оба случая. Особенно интересен второй способ вращения, он вызывает наибольшие затруднения, но на самом деле решение практически такое же, как и в более распространенном вращении вокруг оси абсцисс. В качестве бонуса я вернусь кзадаче нахождения площади фигуры, и расскажу вам, как находить площадь вторым способом – по оси Начнем с наиболее популярной разновидности вращения.
Вычисление объема тела, образованного вращением Пример 1 Вычислить объем тела, полученного вращением фигуры, ограниченной линиями Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости Чертёж здесь довольно прост:
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси
Поиск по сайту: |
 на отрезке
на отрезке 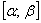 . Величина
. Величина  на том же промежутке
на том же промежутке 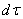 промежутка
промежутка  равно бесконечно малому «кусочку»
равно бесконечно малому «кусочку»  от разыскиваемого значения
от разыскиваемого значения  .
.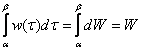 .
. . Стандарты нарушены только для лучшего понимания материала.
. Стандарты нарушены только для лучшего понимания материала. криволинейной трапеции равна определённому интегралу
криволинейной трапеции равна определённому интегралу 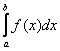 . Ведь что такое произведение
. Ведь что такое произведение  ? Данное произведение выражает площадь прямоугольника с высотой
? Данное произведение выражает площадь прямоугольника с высотой 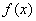 и бесконечно малой длиной
и бесконечно малой длиной 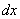 . Иными словами, это элементарный «кирпичик» площади:
. Иными словами, это элементарный «кирпичик» площади: 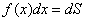 .
.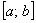 , мы и получаем площадь всей криволинейной трапеции:
, мы и получаем площадь всей криволинейной трапеции:  .
.
 и выполним чертёж. Ввиду симметрии тела достаточно вычислить объём в 1-ом октанте:
и выполним чертёж. Ввиду симметрии тела достаточно вычислить объём в 1-ом октанте: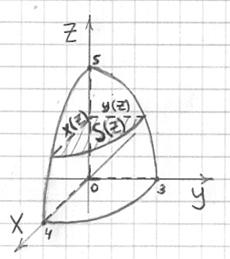
 – она представляет собой «четвертинку» эллипса с большой полуосью
– она представляет собой «четвертинку» эллипса с большой полуосью  и малой полуосью
и малой полуосью 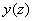 , длины которых зависят от значения «зет». Сама площадь
, длины которых зависят от значения «зет». Сама площадь  , а вместе с ними и площадь
, а вместе с ними и площадь  :
:  . В Примере №2 урока о площади и объеме при параметрически заданной линии выведена формула площади эллипса
. В Примере №2 урока о площади и объеме при параметрически заданной линии выведена формула площади эллипса  . У нас же одна четверть эллипса, поэтому площадь «на нулевом этаже» будет составлять
. У нас же одна четверть эллипса, поэтому площадь «на нулевом этаже» будет составлять 
 не выродятся в точку; площадь здесь станет нулевой:
не выродятся в точку; площадь здесь станет нулевой:  .
. данного тела? Трудность состоит в том, что стОит нам чуть-чуть «дёрнуться» и площадь эллипса изменится. Что делать? Использовать общий принцип интегрирования:
данного тела? Трудность состоит в том, что стОит нам чуть-чуть «дёрнуться» и площадь эллипса изменится. Что делать? Использовать общий принцип интегрирования: . При этом произведение площади
. При этом произведение площади  .
. объёма:
объёма:  – получая тем самым итоговый объём тела.
– получая тем самым итоговый объём тела.



 :
:
 часть эллипсоида, результат умножаем на 8.
часть эллипсоида, результат умножаем на 8.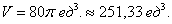
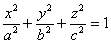 (в общем виде), то получится формула объема эллипсоида:
(в общем виде), то получится формула объема эллипсоида: 
 до
до  , если известен закон изменения его скорости
, если известен закон изменения его скорости  (м/с)
(м/с) расстояние, пройдённое телом за 5 – 2 = 3 секунды – начиная с момента времени
расстояние, пройдённое телом за 5 – 2 = 3 секунды – начиная с момента времени  метр. Но у нас движение даже не равноускоренное (при котором ещё можно извернуться без матана) – у нас закон изменения скорости нелинейный. При этом в начальный момент времени скорость равна
метр. Но у нас движение даже не равноускоренное (при котором ещё можно извернуться без матана) – у нас закон изменения скорости нелинейный. При этом в начальный момент времени скорость равна  м/с, а в конечный момент:
м/с, а в конечный момент:  м/с. Но от этой информации легче не стало – какое расстояние
м/с. Но от этой информации легче не стало – какое расстояние 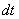 , на котором скорость тела можно считать постоянной (или, как говорят физики,мгновенной). Тогда произведение данной скорости на промежуток времени
, на котором скорость тела можно считать постоянной (или, как говорят физики,мгновенной). Тогда произведение данной скорости на промежуток времени  (скорость умножить на время – это же расстояние, верно?).
(скорость умножить на время – это же расстояние, верно?).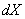 на временнОм промежутке
на временнОм промежутке 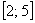 :
:
 ;
;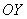 .
. ,
,  вокруг оси
вокруг оси  необходимо построить фигуру, ограниченную линиями
необходимо построить фигуру, ограниченную линиями