 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Приближенное вычисление определенных интегралов ⇐ ПредыдущаяСтр 8 из 8
Важным средством вычисления определенных интегралов является формула Ньютона – Лейбница. Однако ее применение на практике связано с существенными трудностями, возникающими при нахождении первообразной в случае усложнения подынтегральной функции. Помимо того в при решении прикладных задач сплошь и рядом встречаются так называемые «неберущиеся» интегралы ( см. п.2.7). Поэтому в приложениях используют приближённые методы вычисления определённых интегралов – так называемые численные методы, позволяющие найти приближенное значение искомого интеграла с требуемой точностью. Эти методы незаменимы также для подавляющего большинства «берущихся» интегралов. Роль численных методов возрастает в связи с возникающими возможностями современной вычислительной техники, реализующей алгоритмы с необходимой скоростью. Формулы приближённого интегрирования называют квадратурными1) формулами Посмотрим на задачу приближённого интегрирования с геометрической точки зрения. Пусть на отрезке Требуется найти приближённое значение интеграла
Задача приближённого вычисления интеграла Опишем принцип построения этой фигуры. Разобьем отрезок
Обозначим длину частичного отрезка
Рис. 2.48 ___________________________ 1) Напомним, квадратура – вычисление площади. трапецию на элементарные части вертикальными отрезками, проведёнными через точки Для уяснения сути приближённого интегрирования рассмотрим при малых Для уяснения сути приближённого интегрирования рассмотрим при малых
Рис. 2.49. Рис. 2.50.
Рис. 2. 51. Рис. 2.52.
Приближённое значение интеграла Наиболее простыми квадратурными формулами являются формулы прямоугольников: формула левых прямоугольников –
формула средних прямоугольников –
формула правых прямоугольников –
Остановимся подробнее на выводе формулы средних прямоугольников. Обозначим через
Рис. 2.53 Метод средних прямоугольников состоит в замене интеграла
Рассмотрим теперь более подробно вывод формулы трапеций. Суммируя приближённые площади всех элементарных криволинейных трапеций, полученных в результате дробления
Вынося множитель
где Приведём ещё одну важную квадратурную формулу – формулу парабол, называемую также формулой Симпсона. Идею формулы Симпсона поясним на примере. Предположим, что функция
при малых зпачениях
Рис. 2.54
Находим площадь параболической трапеции:
Приближённая формула
носит название малой формулы Симпсона, или малой формулы парабол. Для вычисления интеграла на чётное число
где
Формула (2.46) называется формулой парабол или формулой Симпсона. Замечание 2.8 Приведённые выше квадратурные формулы получены нами в предположении неотрицательности функции Нетрудно доказать, что эти формулы остаются справедливыми также и в общем случае. Замечание 2.9. Без рассмотрения вопроса об оценке погрешности квадратурные формулы носят лишь качественный характер. Приведём без доказательства оценки погрешностей приведённых выше квадратичных формул .
Здесь
Пример 2.24.Вычислить интеграл
Решение.Поскольку число
Таблица
Подынтегральная функция
Поиск по сайту: |
 задана непрерывная функция
задана непрерывная функция 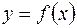 . Предположим дополнительно, что
. Предположим дополнительно, что 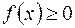 на
на 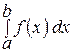
 в этом случае равносильна задаче приближённого вычисления площади криволинейной трапеции под кривой
в этом случае равносильна задаче приближённого вычисления площади криволинейной трапеции под кривой 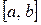 на
на  равных частей точками:
равных частей точками:
 . Разобьём криволинейную
. Разобьём криволинейную
 дробления отрезка
дробления отрезка  интеграл
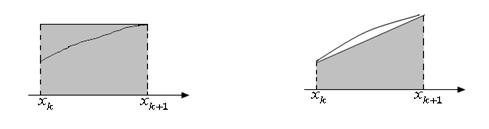
интеграл  – элементарный интеграл, представляющий собой площадь узкой криволинейной трапеции (элементарной криволинейной трапеции, изображённой на рис.2.48). Заменим элементарную криволинейную трапецию прямоугольниками: левым (рис. 2.31); средним рис.2.32); правым (рис.2.33) и прямолинейной трапецией (рис.2.34). В результате получим формулы для приближённого вычисления элементарного интеграла
– элементарный интеграл, представляющий собой площадь узкой криволинейной трапеции (элементарной криволинейной трапеции, изображённой на рис.2.48). Заменим элементарную криволинейную трапецию прямоугольниками: левым (рис. 2.31); средним рис.2.32); правым (рис.2.33) и прямолинейной трапецией (рис.2.34). В результате получим формулы для приближённого вычисления элементарного интеграла





 отрезка
отрезка  (2.41)
(2.41) (2.42)
(2.42) (2.43)
(2.43) - середину отрезка
- середину отрезка 

 интегральной суммой следующего вида
интегральной суммой следующего вида
 равных частей, приходим к соотношению
равных частей, приходим к соотношению

 , заметим, что все слагаемые данной суммы, отличные от
, заметим, что все слагаемые данной суммы, отличные от  и
и  , встречаются в ней дважды. Приводя подобные члены, окончательно получаем
, встречаются в ней дважды. Приводя подобные члены, окончательно получаем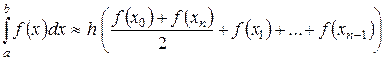 ,
,
 ,
,  ,
,  . Формула (2.44) носит название формулы трапеций.
. Формула (2.44) носит название формулы трапеций. непрерывна на отрезке
непрерывна на отрезке  . Вычислим приближённое значение интеграла
. Вычислим приближённое значение интеграла
 . Выберем на кривой
. Выберем на кривой 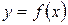 три точки: начальную
три точки: начальную  среднюю
среднюю  и конечную
и конечную 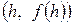 . Заменим кривую
. Заменим кривую  , проходящей через эти точки. Подставим координаты перечисленных точек в уравнение параболы и вычислим параметры
, проходящей через эти точки. Подставим координаты перечисленных точек в уравнение параболы и вычислим параметры 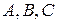 :
:
 ,
,  ,
, 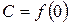
 .
. (2.45)
(2.45) равных частей и применим к каждому интегралу
равных частей и применим к каждому интегралу 
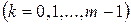 формулу (2.45). В результате получим формулу
формулу (2.45). В результате получим формулу , (2.46)
, (2.46)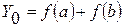 ,
,  ,
,  .
.


 – абсолютная погрешность квадратичных формул.
– абсолютная погрешность квадратичных формул. и
и  – максимальные значения модулей второй
– максимальные значения модулей второй  и четвёртой
и четвёртой  производных подынтегральной функции
производных подынтегральной функции  ,
, 
 по формуле средних прямоугольников, по формуле трапеций, и по формуле Симпсона. Оценить погрешность вычислений при
по формуле средних прямоугольников, по формуле трапеций, и по формуле Симпсона. Оценить погрешность вычислений при  .
.
















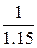








 . Используя квадратурные формулы, получаем следующие значения данного интеграла:
. Используя квадратурные формулы, получаем следующие значения данного интеграла: