|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интегрирование неравенства
Если для непрерывных на отрезке Пусть
Переходя в этом неравенстве к пределу при Итак,
Доказанное утверждение имеет простой геометрический смысл для функций, принимающих на отрезке
Рис. 2.12 Оценки интегралов
Пусть функция
где
Используя далее свойство интеграла от постоянной функции (формулу (2.9)) нетрудно убедиться в справедливости соотношения (2.11). Соотношение (2.11) имеет простой геометрический смысл ( рис.2.13): значение определённого интеграла от неотрицательной на отрезке сверху – величиной площади прямоугольника с основанием высотой снизу – величиной площади прямоугольника с основанием высотой
Рис.2.13
Из рисунка (2.13) видно, что оценка (2.11) может оказаться очень грубой. Она удовлетворительна только тогда, когда на большей части отрезка Пример 2.4. Оценим интеграл Решение. Далее (п. 2.12) будет доказано, что
Интеграл вычисляет площадь криволинейного треугольника, ограниченного сверху графиком функции
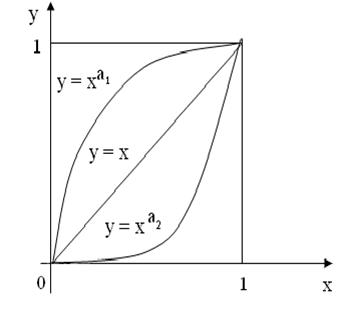
Рис. 2.14.
В этом случае
Если
т.е. верхняя оценка данного интеграла почти совпадает с его истинным значением. Однако с возрастанием показателя степени
При
Ещё более грубой оценка (2.11) может оказаться в тех случаях, когда функция Пример 2.5.Оценить интегралы Решение. Поскольку на отрезке
Полученные оценки являются грубыми (рис. 2.15). Далее будет показано, что
Рис. 2.15. Пример 2.6. Оценить интеграл Решение. Нетрудно убедиться в том, что подынтегральная функция
Таким образом, мы выяснили, что значение данного интеграла заключено между числами 0.5 и 0.71. Отметим, что более точные приёмы показывают, что данный интеграл равен 0.62.
Теорема о среднем
Определение 2.2. Средним значением интегрируемой на отрезке
Теорема 2.2. (О среднем значении). Если функция
Доказательство. По свойству функции, непрерывной на отрезке, (первая теорема Вейерштрасса) для произвольного значения
Положим
Итак, на отрезке, принимает любое значение, заключённое между её наименьшим и наибольшим значениями (теорема о промежуточном значении). Поэтому, в частности, на отрезке Замечание 2.4. Пусть Формулу (2.15) называют формулой среднего значения.
Рис. 2.16
2.17. Интеграл с переменным верхним пределом.
Если функция Определение 2.3.Функцию
называют интегралом с переменным верхним пределом.
Пусть
Рис. 2.17
Рассмотрим свойства интеграла с переменным верхним пределом Теорема 2.3. Если функция Доказательство. Пусть
По теореме о среднем найдётся такая точка
Переходя в последнем равенстве к пределу при теоремы о пределах, получим
что и доказывает непрерывность функции Теорема 2.4. Пусть функция
Доказательство. Воспользуемся равенством (2.16) из доказательства теоремы 2.3. Тогда
где Рассмотрим геометрическую интерпретацию доказательства теоремы 2.4. Пусть
Поиск по сайту: |
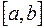 функций
функций 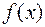 и
и 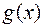 всюду на
всюду на 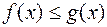 , то обе части этого неравенства можно интегрировать почленно, т.е.. выполнено соотношение
, то обе части этого неравенства можно интегрировать почленно, т.е.. выполнено соотношение ,
,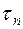 - дробление отрезка
- дробление отрезка 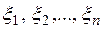 оснащение дробления
оснащение дробления 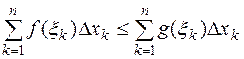 .
.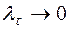 , получим соответствующее неравенство для интегралов.
, получим соответствующее неравенство для интегралов.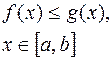


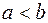 ),и всюду на этом отрезке имеет место неравенство
),и всюду на этом отрезке имеет место неравенство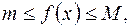
 и
и  – некоторые числа. Тогда
– некоторые числа. Тогда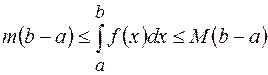 (2.11).
(2.11).
 В силу п. 2.13 имеем
В силу п. 2.13 имеем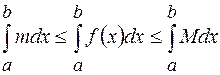
 , т. е. величина площади фигуры ограниченной сверху графиком этой функции оценивается :
, т. е. величина площади фигуры ограниченной сверху графиком этой функции оценивается :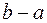 и
и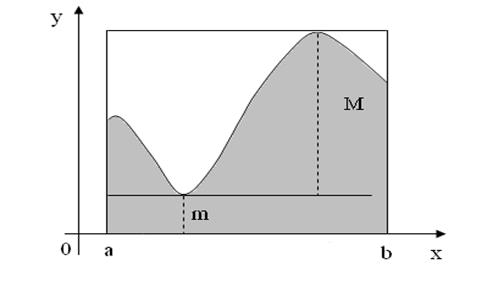
 от степенной функции.
от степенной функции. (2.12)
(2.12)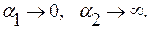
 и оценка (2.11) принимает вид
и оценка (2.11) принимает вид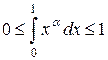 (2.13)
(2.13) – малое положительное число, то криволинейный треугольник «почти заполняет» квадрат и
– малое положительное число, то криволинейный треугольник «почти заполняет» квадрат и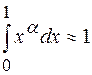 ,
,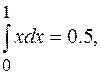
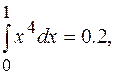 ……….
………. 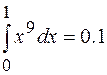 и т.д.
и т.д. правая часть в (2.12) уже вдвое больше левой, а при очень больших значениях
правая часть в (2.12) уже вдвое больше левой, а при очень больших значениях 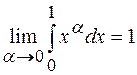 ,
,  (2.14)
(2.14)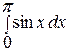 и
и 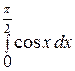
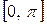
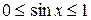 , а на отрезке
, а на отрезке 
 получаем оценки
получаем оценки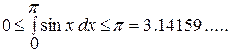
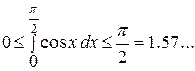
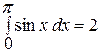 ,
, 
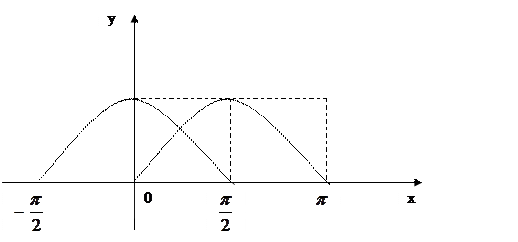
 .
.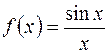 убывает на промежутке
убывает на промежутке 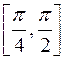 и поэтому в силу (2.11) имеем, что
и поэтому в силу (2.11) имеем, что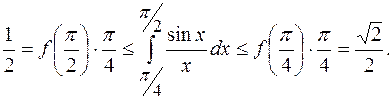
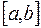 функции
функции 
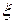 , в которой функция принимает среднее на этом отрезке значение, т.е.
, в которой функция принимает среднее на этом отрезке значение, т.е.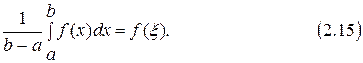
 из
из 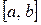 справедливо соотношение
справедливо соотношение  , где
, где  .
.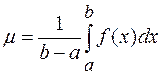 .
. – некоторое число из промежутка
– некоторое число из промежутка 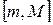 . Но функция, непрерывная
. Но функция, непрерывная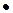
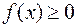 на
на 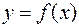 на
на 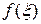 и
и 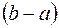 (рис. 2.16).
(рис. 2.16).
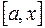 , вложенном в
, вложенном в 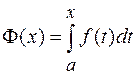

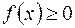 на отрезке
на отрезке 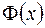 в точке
в точке 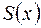 под кривой
под кривой  на отрезке
на отрезке 
 таково, что
таково, что  .
. 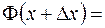
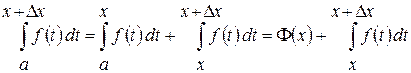
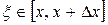 , что
, что 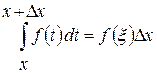 и, следовательно,
и, следовательно,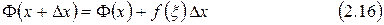
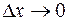 и используя
и используя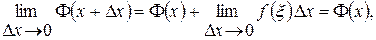
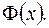
 . (2.17)
. (2.17)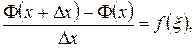 (2.18)
(2.18)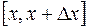 . Переходя в последнем равенстве к пределу при
. Переходя в последнем равенстве к пределу при 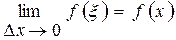 , приходим к (2.16).
, приходим к (2.16). 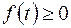 на
на 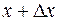 . По теореме о среднем на отрезке
. По теореме о среднем на отрезке 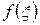 и
и 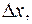 т.е.
т.е. 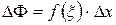 и приходим к (2.18). При
и приходим к (2.18). При