 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определённый интеграл и объёмы тел вращения
Пусть на отрезке
Рис. 2.35 Для решения задачи применим тот же подход, который был использован выше для нахождения площади криволинейной трапеции. Разобьем отрезок
где Геометрический смысл суммы (2.28) – объём тела, составленного из цилиндров с радиусами оснований
где
Примеры 2.16. На рисунках2.36 – 2.38изображены плоские геометрические фигуры: прямоугольник, треугольник и полукруг. В результате вращения этих фигур вокруг оси
Напомним формулы стереометрии.
Рис. 2.38
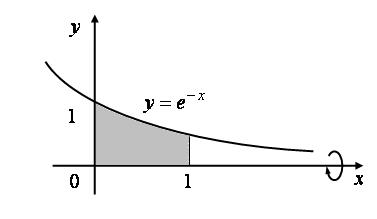
Пример 2.17. Вычислить объем тела, полученного от вращения фигуры, ограниченной линиями
Рис. 2.39
Решение.По формуле (2.30) искомый объем
Пример 2.18. Вычислить объем тела, полученного при вращении вокруг оси
Рис. 2.40.
Решение. Поскольку функция
Формально заменяя в формуле (2.30) переменную
Рис. 2.41. Пример 2.19. Найти объём тела, полученного при вращении вокруг оси ординат фигуры, ограниченной линиями:
Рис.2.42. Решение.Применяя формулу (2.31), получаем
Пример 2.20.Найти объем тела, полученного от вращения вокруг оси ординат плоской фигуры, ограниченной линиями
Рис.2.43.
Решение.Проецируя вращаемую фигуру на ось ординат (рис.2.43), убеждаемся, что искомый
Окончательно
Поиск по сайту: |
 задана непрерывная знакопостоянная функция
задана непрерывная знакопостоянная функция 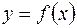 . Необходимо найти объем
. Необходимо найти объем  тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями
тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями  ,
,  ,
,  (рис. 2.35).
(рис. 2.35).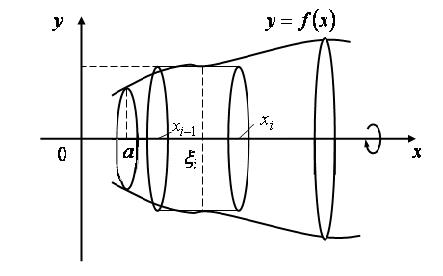
 и на каждом из отрезков разбиения
и на каждом из отрезков разбиения 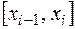 некоторым образом выберем точку
некоторым образом выберем точку  , где
, где  . Тогда некоторое приближение для искомого объема даст следующая сумма
. Тогда некоторое приближение для искомого объема даст следующая сумма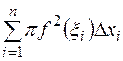 ,
,
 ,
, 
 ,
,  ,….,
,….,  и высотами
и высотами  соответственно (рис.2.35). Очевидно, что приближение для искомого объема
соответственно (рис.2.35). Очевидно, что приближение для искомого объема 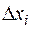 отрезков разбиения
отрезков разбиения  . Поэтому за искомый объем
. Поэтому за искомый объем  (2.29)
(2.29) - максимальная из длин отрезков разбиения. Но выражение, состоящее в правой части (2.29), не что иное, как предел интегральной суммы для функции
- максимальная из длин отрезков разбиения. Но выражение, состоящее в правой части (2.29), не что иное, как предел интегральной суммы для функции  , поэтому (см. определение 2.1 и формулу (2.6)) окончательно получаем
, поэтому (см. определение 2.1 и формулу (2.6)) окончательно получаем (2.30)
(2.30) получаются объёмные фигуры -– цилиндр, конус и шар соответственно. Вычислим объёмы этих тел с помощью формулы (2. 30)
получаются объёмные фигуры -– цилиндр, конус и шар соответственно. Вычислим объёмы этих тел с помощью формулы (2. 30) Рис. 2.36.
Рис. 2.36.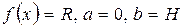 ,
, 
 – объём цилиндра (
– объём цилиндра (  – радиус основания,
– радиус основания, 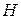 – высота цилиндра);
– высота цилиндра);  – объём конуса (
– объём конуса (  – объём шара.
– объём шара.  Рис.2.37.
Рис.2.37.



 ,
,  ,
, 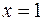 вокруг оси
вокруг оси  .
.
 .
. и одной аркой синусоиды (рис. 2.40).
и одной аркой синусоиды (рис. 2.40).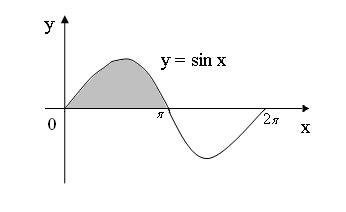
 является
является  -периодической, для вычисления нужного объёма достаточно рассмотреть её на отрезке
-периодической, для вычисления нужного объёма достаточно рассмотреть её на отрезке 
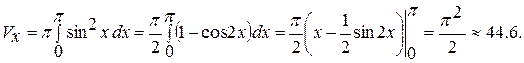
 на
на  получаем формулу для вычисления объёма
получаем формулу для вычисления объёма 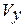 тела, полученного при вращении криволинейной трапеции вокруг оси ординат:
тела, полученного при вращении криволинейной трапеции вокруг оси ординат: (2.31)
(2.31)
 ,
,  ,
,  (рис. 2.39).
(рис. 2.39).



 ,
, 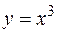 .
.
 равен разности двух объемов: объема
равен разности двух объемов: объема  , полученного от вращения вокруг оси ординат фигуры, ограниченной линиями
, полученного от вращения вокруг оси ординат фигуры, ограниченной линиями  ,
,  , и объема
, и объема  , для которого вращаемая фигура ограничена линиями
, для которого вращаемая фигура ограничена линиями 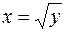 ,
,  , предполагающем переменную
, предполагающем переменную  независимой). Применяя (2.31), получаем:
независимой). Применяя (2.31), получаем: ,
, .
. .
.