 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Внутренне диффузионная область
Сг С Сг
Сц=0
Рисунок 15. Схематичное изображение профиля концентрации газа при условии Сц = 0 и Сп » Сг >> Сц. Внутренне диффузионная область.
ЛЕКЦИЯ 8 Более распространенной является модель с фронтальным перемещением зоны реакции.Согласно этой модели химическая реакция сначала протекает на внешней поверхности частицы, и до тех пор, пока внешний слой твердого реагента полностью не превратиться в соответствующие твердые продукты реакции, более глубинные слои не вступают в реакцию. Постепенно зона химической реакции продвигается внутрь, оставляя за собой твердый продукт реакции и инертную часть исходного твердого вещества (золу). В произвольный момент времени твердая частица представляет собой внутреннее ядро, окруженное внешней оболочкой. Ядро состоит из непрореагировавшего реагента (поэтому эту модель иногда называют моделью с непрореагировавшим ядром). Окружающая его оболочка состоит из твердого продукта и инертных веществ.
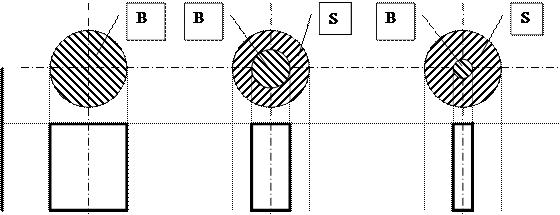
а б в Рисунок 16. Профиль изменения концентрации твердого реагента В по мере протекания гетерогенного процесса, описываемого моделью с фронтальным перемещением зоны реакции: а – до реакции; б – в промежуточный момент реакции; в – почти полностью превращенная частица. Гетерогенный процесс, описываемый моделью с фронтальным перемещением зоны реакции, можно разделить на пять основных стадий. 1. Внешняя диффузия – подвод реагента к поверхности твердой частицы через слой газа, обедненный этим компонентом. 2. Внутренняя диффузия – проникновение газообразного реагента через поры твердого продукта реакции к ядру твердого реагента. 3. Химическая реакция на поверхности непрореагировавшего ядра. 4. Внутренняя диффузия газообразных продуктов через слой твердых продуктов. 5. Внешняя диффузия газообразных продуктов в ядро газового потока. Стадию 4 и 5 в ряде случаев из рассмотрения можно исключить, например когда отсутствуют газообразные продукты реакции или когда протекающая химическая реакция является необратимой. Все эти явления (стадии) протекают в соответствующей последовательности и их можно считать цепочкой последовательных сопротивлений тормозящих суммарную реакцию. Вследствие этого любой этап с максимальным сопротивлением рассматривается как лимитирующая стадия. При анализе процесса необходимо выбирать один фактор, который определяет скорость взаимодействия газа с твердой частицей и который является наиболее чувствительным к изменению условий проведения процесса. Мы рассмотрим только необратимые химические реакции при отсутствии этапов 4 и 5, и только для сферических частиц. Моделирование уравнений для частиц другой правильной формы (цилиндр, таблетки) не вызывает особых затруднений. При частицах с неправильной геометрической формой, анализ модели химического взаимодействия представляет собой сложную задачу. Итак, определим скорость взаимодействия отдельной сферической частицы при условии переноса реагентов через пограничную пленку и при диффузии их через слой продуктов реакции.
С
СГН
R r 0 r R Рисунок 17. Профиль концентрации газа вблизи поверхностного слоя частицы с учетом сопротивления пограничной газовой пленки. 1 – газовая пленка, окружающая частицу (пограничный, диффузионный слой); 2 – слой продуктов реакции (зола); 3 – уменьшенное ядро частицы. СГН – концентрация газа снаружи; СГЗ – концентрация газа на поверхности золы; СГЯ – концентрация газа на поверхности ядра. График показывает, что на поверхности ядра частицы газ отсутствует (СГЗ = СГЯ = 0) и следовательно концентрационная движущаяся сила СГН – СГЗ= СГН. Таким образом концентрационная движущая сила будет неизменной в течение всего периода взаимодействия твердой частицы с газом. Рассмотрим реакцию UO3 + H2 = UO2 + H2O. Тогда уравнение скорости реакции:
где S – площадь поверхности, при условии, что она постоянна. dNUO3 = dNH2 . Количество UO3 можно представить как произведение объема ядра VUO3 на молярно объемную плотность rUO3 , что по сути является молярной концентрацией UO3 в кмоль/м3: NUO3 = VUO3 × rUO3 . Так как твердая частица имеет сферическую форму, то VUO3 = 4/3 ×pr3. Уменьшение объема или радиуса невзаимодействующего ядра эквивалентно исчезновению из зоны реакции dNUO3 молей, тогда:
Поверхность S, к отрой отнесена скорость внешней диффузии, это внешняя поверхность твердой частицы с радиусом R:
Подставляя dNUO3 из уравнения (71) в уравнение (72), получим
Решим дифференциальное уравнение (73):
Отношение (r/R)3 можно заменить на отношение объема непрореагировавшего ядра к объему всей твердой частицы (VUO3/V0 = (r/R)3) и умножив числитель и знаменатель на × rUO3 получим:
где V0 – полный объем твердой частицы неменяющихся размеров. Преобразуем уравнение (75):
Обозначим время, за которое частица полностью прореагирует, через tП, при этом r = 0. При aUO3 = 1 (весь UO3 прореагировал) уравнение (77) позволяет определить время полного превращения твердой частицы:
Следовательно, для внешнедиффузионной области протекания гетерогенной реакции зависимость между t и aUO3 имеет линейный характер:
a

t/tП Рисунок 18. Графическая зависимость степень реагирования от t/tП. 1- скорость процесса лимитируется диффузией через пограничный слой. 3 – скорость процесса лимитируется диффузией газа через слой продуктов реакции (золы). 2 – промежуточный случай.
Поиск по сайту: |
 Сц = 0 и Сп » Сг >> Сц. Процессы внешней диффузии и внутренней диффузии в порах резко отличаются. В первом случае вещество на пути к поверхности не расходуется и любая точка контурной поверхности равнодоступна для диффундирующего газа. При внутренней диффузии, реагент проникая в поры твердой частицы взаимодействует на разных участках, причем разные участки поверхности пор для газа не одинаково доступны. Характер диффузии в порах может быть различным в зависимости от соотношения их диаметра и средней длины свободного пробега молекул диффундирующего газа.
Сц = 0 и Сп » Сг >> Сц. Процессы внешней диффузии и внутренней диффузии в порах резко отличаются. В первом случае вещество на пути к поверхности не расходуется и любая точка контурной поверхности равнодоступна для диффундирующего газа. При внутренней диффузии, реагент проникая в поры твердой частицы взаимодействует на разных участках, причем разные участки поверхности пор для газа не одинаково доступны. Характер диффузии в порах может быть различным в зависимости от соотношения их диаметра и средней длины свободного пробега молекул диффундирующего газа.



 Сп Сп
Сп Сп



 Диффузия газа через пограничную пленку, как лимитирующая стадия процесса.
Диффузия газа через пограничную пленку, как лимитирующая стадия процесса.



 0
0 (70)
(70) (71)
(71)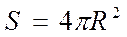 (72)
(72) (73)
(73) (74)
(74) 
 ,
,  (75)
(75) (76)
(76) (77)
(77) (78)
(78)



 (79)
(79)
