 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Выбор оптимальной периодичности диагностирования
Критерий «надёжность – затраты». Целесообразно использовать данный критерий, если отказ системы приводит к невыполнению ответственных функций и последствия отказов этого класса систем не удаётся оценить экономически. Доминирующий фактор в данном случае при оценке отказов - факт невыполнения заданий. С учётом того факта, что система признавалась работоспособной. Критерий максимума технического использования или коэффициента готовности. Целесообразно использовать данный критерий, если материальный ущерб от отказа системы не удаётся оценить количественно и её функционирование не связанно с использованием ответственных функций. При непрерывном режиме работы системы следует применять коэффициент технического использования. Критерий оптимизации периодичности изделия основывается на максимальных значениях коэффициентов при ограничениях на удельные затраты или при минимизации эксплуатационных издержек. Выбор критерия оптимизации основывается на системе классификации систем по признакам, установленным для выбора оптимальной периодичности диагностирования.
Модель Марковского случайного процесса для определения оптимальной периодичности диагностирования. Для определения оптимальной периодичности диагностирования может быть использована Модель Марковского случайного процесса для определения оптимальной периодичности диагностирования для получения зависимости Модель может быть использована для получения зависимости технического использования от периодичности диагностирования и получения оптимального значения данного коэффициента. (рисунок)
μ- интенсивность устранения отказа, перевода изделия в исправное состояния. ν = Интенсивность диагностирования и восстановления неисправностей Интенсивность устранения отказа (импульсный синхронизатор, столбцы-элементарная проверка S-блок. 6 строк.s1-состояние до отказа.) Ориентированный граф строится по известным состоянием, принятым к различению, объекта диагностирования.Интенсивности переходов из состояния в состояния предполагается известными. 1/час. Составляется с-ма уравнений Колмогорова- Чепмена из решений которой находятся зависимости Заключение: определяется максимальное значение коэффициента периодичности диагностирования от… С-ма уравнений Колмогорова Чепмена:
Вывод: оптимальное значение Тд может быть получена путем вычисления на ЭВМ и построения зависимости
Сложные модели могут включать значительно большее число учитываемых состояний в котором может находится объект диагностирования.
S1- исправен S2- работоспособен S3- объект тд функционирует, в нем имеется неявный отказ S4- отказал S5- диагностируется исправный S6- диагностируется работоспособность объекта ТД с вероятностью обнаружения дефекта Pод S7-восстанавливается исправное состояние ОТД с коэффициентом восстановления исправности. Кв. и. S8-диагностируется функционирующий с вероятностью Pо.о. (вероятность обнаружения отказа).
ЭТТА- интенсивность диагностирования η
Поиск по сайту: |

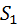 – объект диагностирования исправен
– объект диагностирования исправен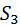 – объект технического диагностирования работоспособен.
– объект технического диагностирования работоспособен.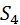 – объект технического диагностирования отказал, он восстанавливается, и приводиться в исправное состояние.
– объект технического диагностирования отказал, он восстанавливается, и приводиться в исправное состояние. – объект технического диагностирования находиться в процессе технического диагностирования, при наличии дефекта он восстанавливается, и приводиться в исправное состояние.
– объект технического диагностирования находиться в процессе технического диагностирования, при наличии дефекта он восстанавливается, и приводиться в исправное состояние.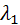 - интенсивность возникновения дефекта
- интенсивность возникновения дефекта
 состояния
состояния 

 - интенсивность отказа.обратно пропорциональна периодичности диагностирования.
- интенсивность отказа.обратно пропорциональна периодичности диагностирования. .
.

 =
= 
 в результате получается зависимости полученные на рисунке
в результате получается зависимости полученные на рисунке 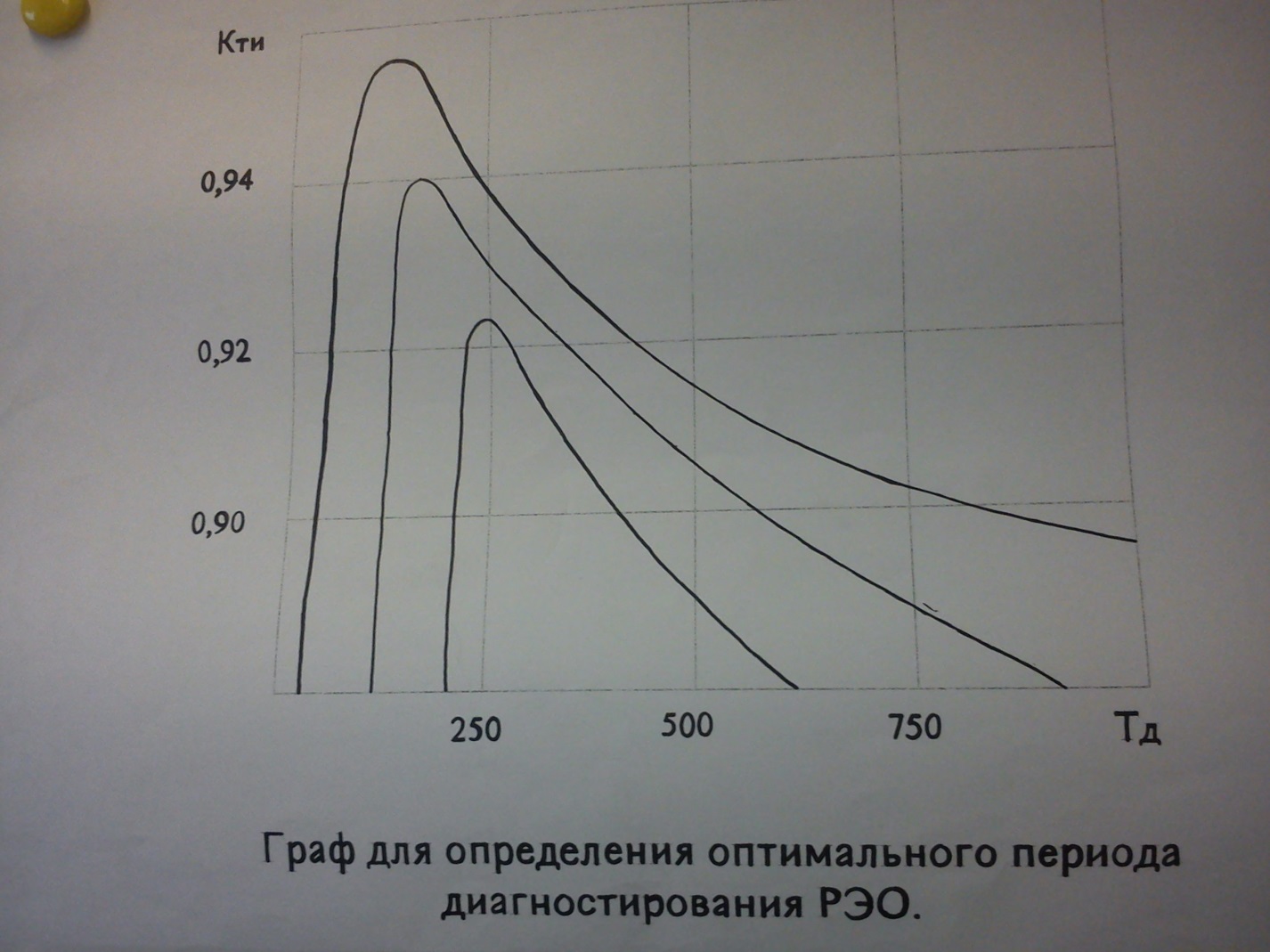
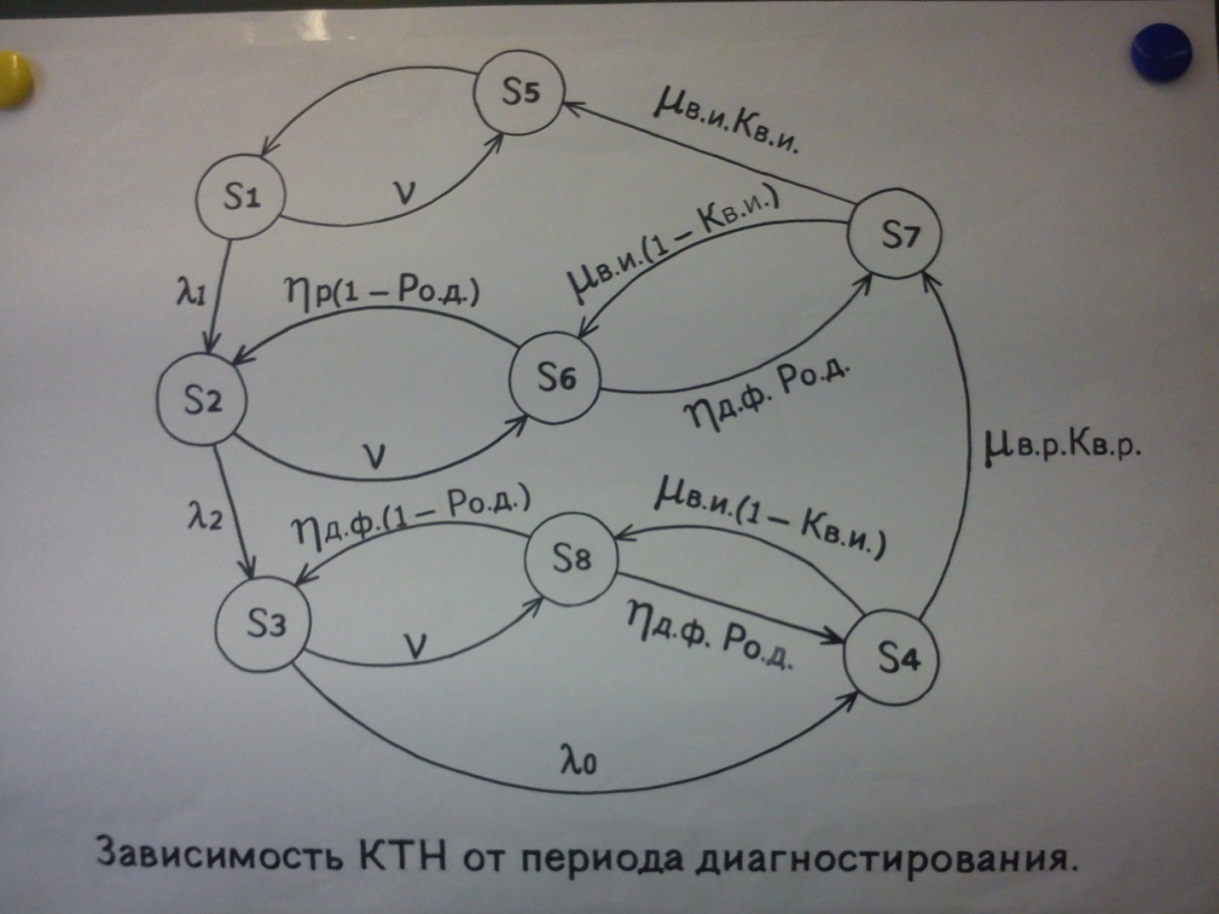
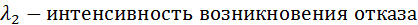 (неявный отказ).
(неявный отказ). возникновения явного отказа
возникновения явного отказа