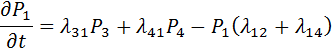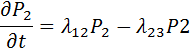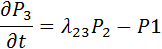|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Модель процессов изменения технических состояний РЭО (модель Марковского процесса)
Переход из одного технического состояния в другое является случайным процессом и присущ РЭО как объекту технического диагностирования. Марковский процесс представляется близкой к реальности и удобной моделью такого процесса, позволяющий связать вероятностные характеристики переходов с параметрами РЭО как объекта технического диагностирования.
P(Si)- вероятность нахождения состояния
Пх из одного состояния в другое является дискретным.
1,2,3,4,5 Система уравнений Колмогорова - Чепмена составляется по следующему правилу, производная вероятности каждого состояния = сумме всех потоков вероятностей ( где Pij- вероятность перехода изделия из состояние Siв Sj. Предполагается что вероятность пребывания изделия в каком либо состоянии вероятность перехода подчиняется экспоненциальному закону Сущность Марковского процесса. Для любого момента времени t вероятность любого технического состояния РЭО Случайны процесс изменения технических состояний удобно представить как переход из состояния в состояние осуществляющийся под воздействием потоков событий, тогда процесс моделирования будет Марковским, если эти потоки событий без последствий и с постоянной интенсивностью. Поток событий или поток вероятностей перехода изделия из одного состояния в другое это величина численно равная (картинка)
Нахождение
Производная вероятности каждого состояния равна сумме всех потоков вероятностей идущих из других состояний в данноеминус сумма всех потоков вероятностей идущих из данного состояния в другие. Такая система дифференциальных уравнений называется системой уравнений Колмогорова-Чепмена.
Решение осуществляется различными методами, в том числе и преобразованием Лапласа. Вероятность нахождения РЭО в различных состояниях подчиняется экспоненциальному закону.
Поиск по сайту: |
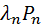 п на лямбда) идущих из другого состояния в данное минус сумма всех потоков вероятностей идущих из данного состояния в другие. Иногда Марковская модель может быть представлена в матричном виде
п на лямбда) идущих из другого состояния в данное минус сумма всех потоков вероятностей идущих из данного состояния в другие. Иногда Марковская модель может быть представлена в матричном виде 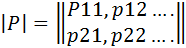
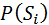 зависит только от её технического состояния в настоящий момент и не зависит от того когда и каким образом оказалось в этом состоянии (только
зависит только от её технического состояния в настоящий момент и не зависит от того когда и каким образом оказалось в этом состоянии (только 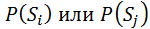 ). Для моделирования выбирается набор дискретных состояний (
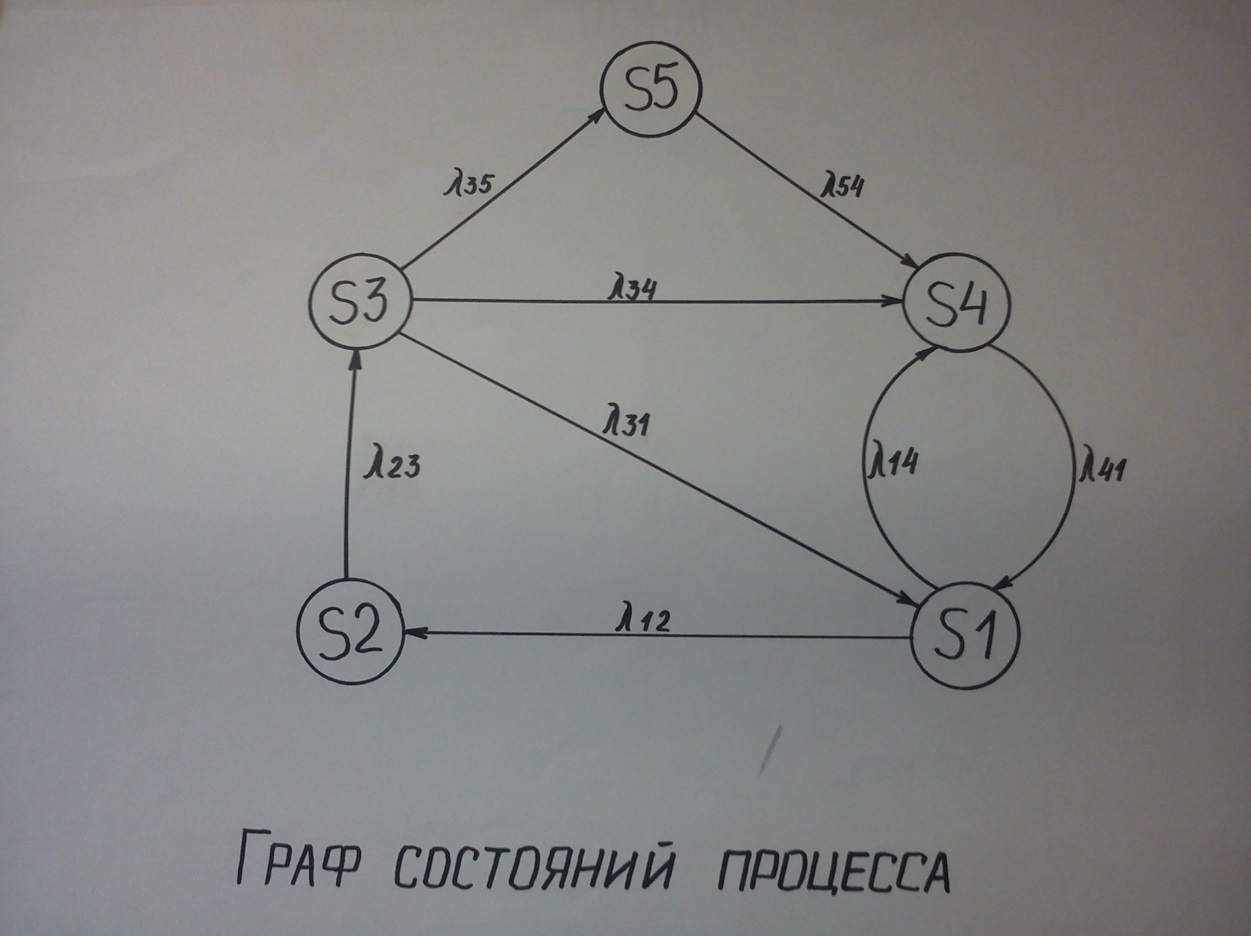
). Для моделирования выбирается набор дискретных состояний (  ),которую удобно иллюстрировать с помощью графасостояний, где дугами указаны возможные переходы, а вершинами – технические состояния. Непрерывная цепь Маркова – модель описания РЭО как объекта технического диагностирования. Как случайный процесс с дискретными состояниями и непрерывным временем, характеристиками переходов является интенсивности переходов (
),которую удобно иллюстрировать с помощью графасостояний, где дугами указаны возможные переходы, а вершинами – технические состояния. Непрерывная цепь Маркова – модель описания РЭО как объекта технического диагностирования. Как случайный процесс с дискретными состояниями и непрерывным временем, характеристиками переходов является интенсивности переходов ( 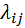 ).
).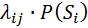 .
.
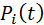 осуществляется решением системы дифференциальных уравнений следующего вида:
осуществляется решением системы дифференциальных уравнений следующего вида:
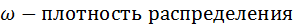
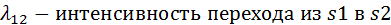
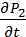 ,
,