 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Проблемы алгоритмов архивации с потерями
Первыми для архивации изображений стали применяться привычные алгоритмы. Те, что использовались и используются в системах резервного копирования, при создании дистрибутивов и т.п. Эти алгоритмы архивировали информацию без изменений. Однако основной тенденцией в последнее время стало использование новых классов изображений. Старые алгоритмы перестали удовлетворять требованиям, предъявляемым к архивации. Многие изображения практически не сжимались, хотя “на взгляд” обладали явной избыточностью. Это привело к созданию нового типа алгоритмов — сжимающих с потерей информации. Как правило, коэффициент архивации и, следовательно, степень потерь качества в них можно задавать. При этом достигается компромисс между размером и качеством изображений. Одна из серьезных проблем машинной графики заключается в том, что до сих пор не найден адекватный критерий оценки потерь качества изображения. А теряется оно постоянно — при оцифровке, при переводе в ограниченную палитру цветов, при переводе в другую систему цветопредставления для печати, и, что для нас особенно важно, при архивации с потерями. Можно привести пример простого критерия: среднеквадратичное отклонение значений пикселов (L2 мера, или root mean square — RMS):
По нему изображение будет сильно испорчено при понижении яркости всего на 5% (глаз этого не заметит — у разных мониторов настройка яркости варьируется гораздо сильнее). В то же время изображения со “снегом” — резким изменением цвета отдельных точек, слабыми полосами или “муаром” будут признаны “почти не изменившимися”. Свои неприятные стороны есть и у других критериев. Рассмотрим, например, максимальное отклонение:
Эта мера, как можно догадаться, крайне чувствительна к биению отдельных пикселов. Т.е. во всем изображении может существенно измениться только значение одного пиксела (что практически незаметно для глаза), однако согласно этой мере изображение будет сильно испорчено. Мера, которую сейчас используют на практике, называется мерой отношения сигнала к шуму (peak-to-peak signal-to-noise ratio — PSNR).
Данная мера, по сути, аналогична среднеквадратичному отклонению, однако пользоваться ей несколько удобнее за счет логарифмического масштаба шкалы. Ей присущи те же недостатки, что и среднеквадратичному отклонению. Лучше всего потери качества изображений оценивают наши глаза. Отличной считается архивация, при которой невозможно на глаз различить первоначальное и разархивированное изображения. Хорошей — когда сказать, какое из изображений подвергалось архивации, можно только сравнивая две находящихся рядом картинки. При дальнейшем увеличении степени сжатия, как правило, становятся заметны побочные эффекты, характерные для данного алгоритма. На практике, даже при отличном сохранении качества, в изображение могут быть внесены регулярные специфические изменения. Поэтому алгоритмы архивации с потерями не рекомендуется использовать при сжатии изображений, которые в дальнейшем собираются либо печатать с высоким качеством, либо обрабатывать программами распознавания образов. Неприятные эффекты с такими изображениями, как мы уже говорили, могут возникнуть даже при простом масштабировании изображения. Алгоритм JPEG JPEG — один из самых новых и достаточно мощных алгоритмов. Практически он является стандартом де-факто для полноцветных изображений [1]. Оперирует алгоритм областями 8х8, на которых яркость и цвет меняются сравнительно плавно. Вследствие этого, при разложении матрицы такой области в двойной ряд по косинусам (см. формулы ниже) значимыми оказываются только первые коэффициенты. Таким образом, сжатие в JPEG осуществляется за счет плавности изменения цветов в изображении. Алгоритм разработан группой экспертов в области фотографии специально для сжатия 24-битных изображений. JPEG — Joint Photographic Expert Group — подразделение в рамках ISO — Международной организации по стандартизации. Название алгоритма читается ['jei'peg]. В целом алгоритм основан на дискретном косинусоидальном преобразовании (в дальнейшем ДКП), применяемом к матрице изображения для получения некоторой новой матрицы коэффициентов. Для получения исходного изображения применяется обратное преобразование. ДКП раскладывает изображение по амплитудам некоторых частот, таким образом, при преобразовании мы получаем матрицу, в которой многие коэффициенты либо близки, либо равны нулю. Кроме того, человеческая система цветового восприятия слабо распознает определенные частоты. Поэтому можно аппроксимировать некоторые коэффициенты более грубо без заметной потери качества изображения. Для этого используется квантование коэффициентов (quantization). В самом простом случае — это арифметический побитовый сдвиг вправо. При этом преобразовании теряется часть информации, но могут достигаться большие коэффициенты сжатия. Как работает алгоритм Итак, рассмотрим алгоритм подробнее. Пусть мы сжимаем 24-битное изображение. Шаг 1. Переводим изображение из цветового пространства RGB, с компонентами, отвечающими за красную (Red), зеленую (Green) и синюю (Blue) составляющие цвета точки, в цветовое пространство YCrCb (иногда называют YUV). В нем Y — яркостная составляющая, а Cr, Cb — компоненты, отвечающие за цвет (хроматический красный и хроматический синий). За счет того, что человеческий глаз менее чувствителен к цвету, чем к яркости, появляется возможность архивировать массивы для Cr и Cb компонент с большими потерями и, соответственно, большими коэффициентами сжатия. Подобное преобразование уже давно используется в телевидении. На сигналы, отвечающие за цвет, там выделяется более узкая полоса частот. Упрощенно перевод из цветового пространства RGB в цветовое пространство YCrCb можно представить так:
Обратное преобразование осуществляется умножением вектора YUV на обратную матрицу.
Шаг 2. Разбиваем исходное изображение на матрицы 8х8. Формируем из каждой три рабочие матрицы ДКП — по 8 бит отдельно для каждой компоненты. При больших коэффициентах сжатия, этот шаг может выполняется чуть сложнее. Изображение делится по компоненте Y — как и в первом случае, а для компонент Cr и Cb матрицы набираются через строчку и через столбец. Т.е. из исходной матрицы размером 16x16 получается только одна рабочая матрица ДКП. При этом, как нетрудно заметить, мы теряем 3/4 полезной информации о цветовых составляющих изображения и получаем сразу сжатие в два раза. Мы можем поступать так благодаря работе в пространстве YCrCb. На результирующем RGB изображении, как показала практика, это сказывается не сильно. Шаг 3. Применяем ДКП к каждой рабочей матрице. При этом мы получаем матрицу, в которой коэффициенты в левом верхнем углу соответствуют низкочастотной составляющей изображения, а в правом нижнем - высокочастотной. В упрощенном виде это преобразование можно представить так:
где
Шаг 4. Производим квантование. В принципе это просто деление рабочей матрицы на матрицу квантования поэлементно. Для каждой компоненты (Y, U и V), в общем случае, задается своя матрица квантования q[u,v] (далее МК).
На этом шаге осуществляется управление степенью сжатия, и происходят самые большие потери. Понятно, что, задавая МК с большими коэффициентами, мы получим больше нулей и, следовательно, большую степень сжатия. В стандарт JPEG включены рекомендованные МК, построенные опытным путем. Матрицы для большего или меньшего коэффициентов сжатия получают путем умножения исходной матрицы на некоторое число gamma. С квантованием связаны и специфические эффекты алгоритма. При больших значениях коэффициента gamma потери в низких частотах могут быть настолько велики, что изображение распадется на квадраты 8х8. Потери в высоких частотах могут проявиться в так называемом “эффекте Гиббса”, когда вокруг контуров с резким переходом цвета образуется своеобразный “нимб”. Шаг 5. Переводим матрицу 8x8 в 64-элементный вектор при помощи “зигзаг”-сканирования, т.е. берем элементы с индексами (0,0), (0,1), (1,0), (2,0)...
Таким образом, в начале вектора мы получаем коэффициенты матрицы, соответствующие низким частотам, а в конце — высоким. Шаг 6. Свертываем вектор с помощью алгоритма группового кодирования. При этом получаем пары типа (пропустить, число), где “пропустить” является счетчиком пропускаемых нулей, а “число” — значение, которое необходимо поставить в следующую ячейку. Так, вектор 42 3 0 0 0 -2 0 0 0 0 1 ... будет свернут в пары (0,42) (0,3) (3,-2) (4,1) ... . Шаг 7. Свертываем получившиеся пары кодированием по Хаффману с фиксированной таблицей. Процесс восстановления изображения в этом алгоритме полностью симметричен. Метод позволяет сжимать некоторые изображения в 10-15 раз без серьезных потерь.
Существенными положительными сторонами алгоритма является то, что: 1) Задается степень сжатия. 2) Выходное цветное изображение может иметь 24 бита на точку. Отрицательными сторонами алгоритма является то, что: 1) При повышении степени сжатия изображение распадается на отдельные квадраты (8x8). Это связано с тем, что происходят большие потери в низких частотах при квантовании, и восстановить исходные данные становится невозможно. 2) Проявляется эффект Гиббса — ореолы по границам резких переходов цветов. Как уже говорилось, стандартизован JPEG относительно недавно — в 1991 году. Но уже тогда существовали алгоритмы, сжимающие сильнее при меньших потерях качества. Дело в том, что действия разработчиков стандарта были ограничены мощностью существовавшей на тот момент техники. То есть даже на персональном компьютере алгоритм должен был работать меньше минуты на среднем изображении, а его аппаратная реализация должна быть относительно простой и дешевой. Алгоритм должен был быть симметричным (время разархивации примерно равно времени архивации). Последнее требование сделало возможным появление таких игрушек, как цифровые фотоаппараты — устройства, размером с небольшую видеокамеру, снимающие 24-битовые фотографии на 10-20 Мб флэш карту с интерфейсом PCMCIA. Потом эта карта вставляется в разъем на вашем лэптопе и соответствующая программа позволяет считать изображения. Не правда ли, если бы алгоритм был несимметричен, было бы неприятно долго ждать, пока аппарат “перезарядится” — сожмет изображение. Не очень приятным свойством JPEG является также то, что нередко горизонтальные и вертикальные полосы на дисплее абсолютно не видны, и могут проявиться только при печати в виде муарового узора. Он возникает при наложении наклонного растра печати на горизонтальные и вертикальные полосы изображения. Из-за этих сюрпризов JPEG не рекомендуется активно использовать в полиграфии, задавая высокие коэффициенты. Однако при архивации изображений, предназначенных для просмотра человеком, он на данный момент незаменим. Широкое применение JPEG долгое время сдерживалось, пожалуй, лишь тем, что он оперирует 24-битными изображениями. Поэтому для того, чтобы с приемлемым качеством посмотреть картинку на обычном мониторе в 256-цветной палитре, требовалось применение соответствующих алгоритмов и, следовательно, определенное время. В приложениях, ориентированных на придирчивого пользователя, таких, например, как игры, подобные задержки неприемлемы. Кроме того, если имеющиеся у вас изображения, допустим, в 8-битном формате GIF перевести в 24-битный JPEG, а потом обратно в GIF для просмотра, то потеря качества произойдет дважды при обоих преобразованиях. Тем не менее, выигрыш в размерах архивов зачастую настолько велик (в 3-20 раз!), а потери качества настолько малы, что хранение изображений в JPEG оказывается очень эффективным. Несколько слов необходимо сказать о модификациях этого алгоритма. Хотя JPEG и является стандартом ISO, формат его файлов не был зафиксирован. Пользуясь этим, производители используют свои, несовместимые между собой форматы, и, следовательно, могут изменить алгоритм. Так, внутренние таблицы алгоритма, рекомендованные ISO, заменяются ими на свои собственные. Кроме того, легкая неразбериха присутствует при задании степени потерь. Например, при тестировании выясняется, что “отличное” качество, “100%” и “10 баллов” дают существенно различающиеся картинки. При этом, кстати, “100%” качества не означает сжатие без потерь. Встречаются также варианты JPEG для специфических приложений. Как стандарт ISO JPEG начинает все шире использоваться при обмене изображениями в компьютерных сетях. Поддерживается алгоритм JPEG в форматах Quick Time, PostScript Level 2, Tiff 6.0 и, на данный момент занимает видное место в системах мультимедиа. Характеристики алгоритма JPEG: Коэффициенты компрессии: 2-200 (Задается пользователем). Класс изображений: Полноцветные 24 битные изображения, или изображения в градациях серого без резких переходов цветов (фотографии). Симметричность: 1 Характерные особенности: В некоторых случаях, алгоритм создает “ореол” вокруг резких горизонтальных и вертикальных границ в изображении (эффект Гиббса). Кроме того, при высокой степени сжатия изображение распадается на блоки 8х8 пикселов. Фрактальный алгоритм Идея метода Фрактальная архивация основана на том, что мы представляем изображение в более компактной форме — с помощью коэффициентов системы итерируемых функций (Iterated Function System — далее по тексту как IFS). Прежде чем рассматривать сам процесс архивации, разберем, как IFS строит изображение, т.е. процесс декомпрессии . Строго говоря, IFS представляет собой набор трехмерных аффинных преобразований, в нашем случае переводящих одно изображение в другое. Преобразованию подвергаются точки в трехмерном пространстве (х_координата, у_координата, яркость). Наиболее наглядно этот процесс продемонстрировал Барнсли в своей книге “Fractal Image Compression”. Там введено понятие Фотокопировальной Машины, состоящей из экрана, на котором изображена исходная картинка, и системы линз, проецирующих изображение на другой экран: · Линзы могут проецировать часть изображения произвольной формы в любое другое место нового изображения. · Области в которые проецируются изображения не пересекаются. · Линза может менять яркость и уменьшать контрастность. · Линза может зеркально отражать и поворачивать свой фрагмент изображения. · Линза должна (масштабировать) уменьшатьсвой фрагмент изображения.
Рисунок. Машина Барнсли Расставляя линзы и меняя их характеристики, мы можем управлять получаемым изображением. Одна итерация работы Машины заключается в том, что по исходному изображению с помощью проектирования строится новое, после чего новое берется в качестве исходного. Утверждается, что в процессе итераций мы получим изображение, которое перестанет изменяться. Оно будет зависеть только от расположения и характеристик линз и не будет зависеть от исходной картинки. Это изображение называется “неподвижной точкой” или аттрактором данной IFS. Соответствующая теория гарантирует наличие ровно одной неподвижной точки для каждой IFS. Поскольку отображение линз является сжимающим, каждая линза в явном виде задает самоподобные области в нашем изображении. Благодаря самоподобию мы получаем сложную структуру изображения при любом увеличении. Таким образом, интуитивно понятно, что система итерируемых функций задает фрактал (нестрого — самоподобный математический объект). Наиболее известны два изображения, полученных с помощью IFS: “треугольник Серпинского” и “папоротник Барнсли”. “Треугольник Серпинского” задается тремя, а “папоротник Барнсли” четырьмя аффинными преобразованиями (или, в нашей терминологии, “линзами”). Каждое преобразование кодируется буквально считанными байтами, в то время как изображение, построенное с их помощью, может занимать и несколько мегабайт.
Упражнение: Укажите в изображении 4 области, объединение которых покрывало бы все изображение и каждая из которых была бы подобна всему изображению (не забывайте про стебель папоротника). Из вышесказанного становится понятно, как работает архиватор, и почему ему требуется так много времени. Фактически, фрактальная компрессия — это поиск самоподобных областей в изображении и определение для них параметров аффинных преобразований.
В худшем случае, если не будет применяться оптимизирующий алгоритм, потребуется перебор и сравнение всех возможных фрагментов изображения разного размера. Даже для небольших изображений при учете дискретности мы получим астрономическое число перебираемых вариантов. Причем, даже резкое сужение классов преобразований, например, за счет масштабирования только в определенное количество раз, не дает заметного выигрыша во времени. Кроме того, при этом теряется качество изображения. Подавляющее большинство исследований в области фрактальной компрессии сейчас направлены на уменьшение времени архивации, необходимого для получения качественного изображения. Далее приводятся основные определения и теоремы, на которых базируется фрактальная компрессия. Этот материал более детально и с доказательствами рассматривается в [3] и в [4]. Определение. Преобразование
где a, b, c, d, e, f действительные числа и Определение. Преобразование
где a, b, c, d, e, f, p, q, r, s, t, u действительные числа и Определение. Пусть Определение. Преобразование
Замечание: Формально мы можем использовать любое сжимающее отображение при фрактальной компрессии, но реально используются лишь трехмерные аффинные преобразования с достаточно сильными ограничениями на коэффициенты.
Поиск по сайту: |

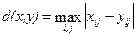














 , представимое в виде
, представимое в виде
 называется двумерным аффинным преобразованием.
называется двумерным аффинным преобразованием. , представимое в виде
, представимое в виде
 называется трехмерным аффинным преобразованием.
называется трехмерным аффинным преобразованием. — преобразование в пространстве Х. Точка
— преобразование в пространстве Х. Точка  такая, что
такая, что  называется неподвижной точкой (аттрактором) преобразования.
называется неподвижной точкой (аттрактором) преобразования. , такое, что
, такое, что