 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Классический алгоритм Хаффмана
Один из классических алгоритмов, известных с 60-х годов. Использует только частоту появления одинаковых байт в изображении. Сопоставляет символам входного потока, которые встречаются большее число раз, цепочку бит меньшей длины. И, напротив, встречающимся редко — цепочку большей длины. Для сбора статистики требует двух проходов по изображению. Для начала введем несколько определений. Определение. Пусть задан алфавит Y={a1, ..., ar}, состоящий из конечного числа букв. Конечную последовательность символов из Y
будем называть словом в алфавите Y, а число n — длиной слова A. Длина слова обозначается как l(A). Пусть задан алфавит W, W={b1, ..., bq}. Через B обозначим слово в алфавите W и через S(W) — множество всех непустых слов в алфавите W. Пусть S=S(Y) — множество всех непустых слов в алфавите Y, и S' — некоторое подмножество множества S. Пусть, также задано отображение F, которое каждому слову A, AÎS(Y), ставит в соответствие слово B=F(A), BÎS(W). Слово В будем назвать кодом сообщения A, а переход от слова A к его коду — кодированием. Определение. Рассмотрим соответствие между буквами алфавита Y и некоторыми словами алфавита W: a1 — B1, Это соответствие называют схемой и обозначают через S. Оно определяет кодирование следующим образом: каждому слову Определение. Пусть слово В имеет вид B=B'B" Тогда слово B' называется началом или префиксом слова B, а B" — концом слова B. При этом пустое слово L и само слово B считаются началами и концами слова B. Определение. Схема S обладает свойством префикса, если для любых i и j (1£i, j£r, i¹j) слово Bi не является префиксом слова Bj. Теорема 1. Если схема S обладает свойством префикса, по алфавитное кодирование будет взаимно однозначным. Предположим, что задан алфавит Y={a1,..., ar} (r>1) и набор вероятностей p1, . . . , pr a1 — B1, обладающих свойством взаимной однозначности. Для каждой схемы можно ввести среднюю длину lср, определяемую как математической ожидание длины элементарного кода:
Длина lср показывает, во сколько раз увеличивается средняя длина слова при кодировании со схемой S. Можно показать, что lср достигает величины своего минимума l* на некоторой S и определена как
Определение. Коды, определяемые схемой S с lср= l*, называются кодами с минимальной избыточностью, или кодами Хаффмана. Коды с минимальной избыточностью дают в среднем минимальное увеличение длин слов при соответствующем кодировании. В нашем случае, алфавит Y={a1,..., ar} задает символы входного потока, а алфавит W={0,1}, т.е. состоит всего из нуля и единицы. Алгоритм построения схемы S можно представить следующим образом: Шаг 1. Упорядочиваем все буквы входного алфавита в порядке убывания вероятности. Считаем все соответствующие слова Bi, из алфавита W={0,1} пустыми. Шаг 2. Объединяем два символа air-1 и air с наименьшими вероятностями pi r-1 и pi r в псевдосимвол a'{air-1 air} c вероятностью pir-1+pir. Дописываем 0 в начало слова Bir-1 (Bir-1=0Bir-1), и 1 в начало слова и Bir (Bir=1Bir). Шаг 3. Удаляем из списка упорядоченных символов air-1 и air, заносим туда псевдосимвол a'{air-1air}. Проводим шаг 2, добавляя при необходимости 1 или ноль для всех слов Bi, соответствующих псевдосимволам, до тех пор, пока в списке не останется 1 псевдосимвол. Пример: Пусть у нас есть 4 буквы в алфавите Y={a1,..., a4} (r=4), p1=0.5, p2=0.24, p3=0.15, p4=0.11
Производя действия, соответствующие 2-му шагу мы получаем псевдосимвол с вероятностью 0.26 (и приписываем 0 и 1 соответствующим словам). Повторяя же эти действия для измененного списка, мы получаем псевдосимвол с вероятностью 0.5. И, наконец, на последнем этапе мы получаем суммарную вероятность 1. Для того, чтобы восстановить кодирующие слова, нам надо пройти по стрелкам от начальных символов к концу получившегося бинарного дерева. Так, для символа с вероятностью p4, получим B4=101, для p3 получим B3=100, для p2 получим B2=11, для p1 получим B1=0. Что означает схему: a1 — 0, Эта схема представляет собой префиксный код, являющийся кодом Хаффмана. Самый часто встречающийся в потоке символ a1 мы будем кодировать самым коротким словом 0, а самый редко встречающийся a4 длинным словом 101. Для последовательности из 100 символов, в которой символ a1 встретится 50 раз, символ a2 — 24 раза, символ a3 — 15 раз, а символ a4 — 11 раз, данный код позволит получить последовательность из 176 бит ( Доказательства теоремы, а также того, что построенная схема действительно задает код Хаффмана смотри в [10]. Как стало понятно из изложенного выше, классический алгоритм Хаффмана требует записи в файл таблицы соответствия кодируемых символов и кодирующих цепочек. На практике используются его разновидности. Так, в некоторых случаях резонно либо использовать постоянную таблицу, либо строить ее “адаптивно”, т.е. в процессе архивации/разархивации. Эти приемы избавляют нас от двух проходов по изображению и необходимости хранения таблицы вместе с файлом. Кодирование с фиксированной таблицей применяется в качестве последнего этапа архивации в JPEG и в рассмотренном ниже алгоритме CCITT Group 3. Характеристики классического алгоритма Хаффмана: Коэффициенты компрессии:8, 1,5, 1 (Лучший, средний, худший коэффициенты) Класс изображений: Практически не применяется к изображениям в чистом виде. Обычно используется как один из этапов компрессии в более сложных схемах. Симметричность: 2 (за счет того, что требует двух проходов по массиву сжимаемых данных). Характерные особенности: Единственный алгоритм, который не увеличивает размера исходных данных в худшем случае (если не считать необходимости хранить таблицу перекодировки вместе с файлом).
Поиск по сайту: |

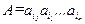 из S'(W)=S(W) ставится в соответствие слово
из S'(W)=S(W) ставится в соответствие слово 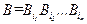 , называемое кодом слова A. Слова B1 ... Br называются элементарными кодами. Данный вид кодирования называют алфавитным кодированием.
, называемое кодом слова A. Слова B1 ... Br называются элементарными кодами. Данный вид кодирования называют алфавитным кодированием.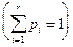 появления символов a1,..., ar. Пусть, далее, задан алфавит W, W={b1, ..., bq} (q>1). Тогда можно построить целый ряд схем S алфавитного кодирования
появления символов a1,..., ar. Пусть, далее, задан алфавит W, W={b1, ..., bq} (q>1). Тогда можно построить целый ряд схем S алфавитного кодирования — длины слов.
— длины слов.
 . Тогда процесс построения схемы можно представить так:
. Тогда процесс построения схемы можно представить так:
 ). Т.е. в среднем мы потратим 1.76 бита на символ потока.
). Т.е. в среднем мы потратим 1.76 бита на символ потока.