|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Расчет основных кинетических и термодинамических параметров химической реакции
Зависимость константы скорости от температуры описывается уравнением Аррениуса (4.1):
k=A0e-Ea/RT (4.1),
где A0 – предэкспоненциальный множитель, Еа – энергия активации, R – универсальная газовая постоянная, T – температура. Если Ea не зависит от температуры, то A0 будет равен константе скорости (k0) при T → ∞. Во многих случаях Ea и A0 слабо зависят от температуры и в небольшом температурном интервале этой зависимостью можно пренебречь.
Если прологарифмировать левую и правую части уравнения (4.1), получим
ln(k) = -Ea/RT+ lnA0 (4.1а),
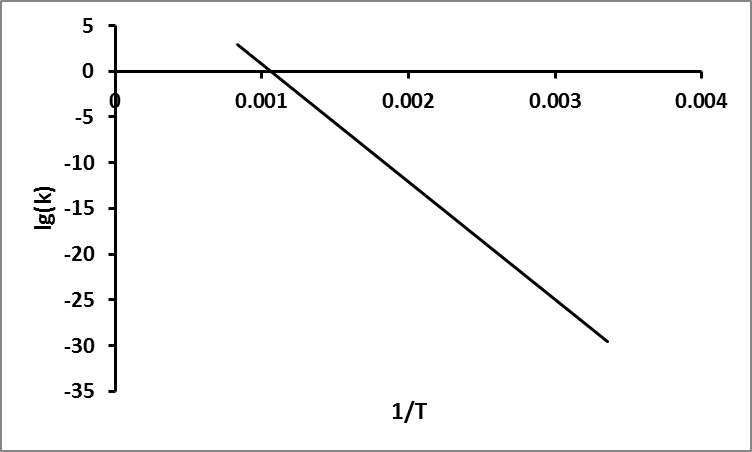
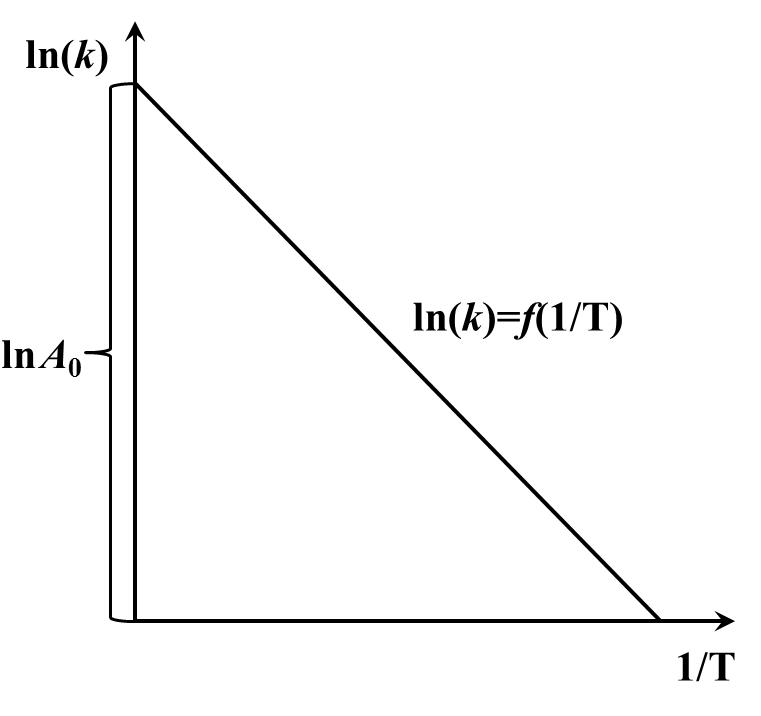
где A0 и Ea – постоянные величины. Следовательно, ln(k)=f(1/T) зависимость ln(k) от 1/T является линейной (См. Рис. 4.3).
Рисунок 4.3 Зависимость ln(k) от обратной температуры
Используя основные представления теории переходного состояния (активированного комплекса) и квантово-химические методы, можно рассчитать константу скорости kT элементарной химической реакции. Важную роль в этих расчетах играет уравнение Эйринга, связывающие константу скорости реакции и константу равновесия Кс≠ образования активированного комплекса [15], выраженную через концентрации
где Kb – константа Больцмана, h – постоянная Планка.
В зависимости от того как рассчитывают константу равновесия образования активированного комплекса различают статистический и термодинамический варианты теории переходного состояния. В статистическом подходе константа равновесия выражается через сумму по состояниям активированного комплекса Q≠ и суммы по состояниям реагентов Qреаг.
где Для идеального газа полную сумму по состояниям можно заменить молекулярными суммами по состояниям, которые можно представить в виде произведения сомножителей, отвечающим различным видам движения
Величина поступательной статистической суммы
где
Величина
где r – межъядерное расстояние, М приведенная масса молекулы, σ = 1 для несимметричных молекул и σ = 2 – для симметричных. В многоатомных молекулах возможен еще один вид движения – вращение одной части молекулы относительно другой. Возможность внутреннего вращения должно учитываться при вычислении общей суммы по состояниям. За счет внутреннего вращения уменьшается число колебательных степеней свободы. В общем случае молекула может иметь S степеней свободы вращательного движения, из них три относятся к вращению молекулы как целого и S-3 к внутреннему вращению. Учет внутреннего вращения достаточно сложная проблема, особенно в случае заторможенного вращения. Метод решения задачи о заторможенном внутреннем вращении в многоатомных молекулах впервые был предложен Питцером [16]. Он показал, что вклад внутреннего вращения в термодинамические функции (например, в теплоемкость и энтропию) можно оценить с помощью специальных, впервые полученных им таблиц. В качестве двух переменных можно взять отношение высоты потенциального барьера U0 к KbT и обратную величину суммы по состояниям свободного вращения 1/Qfr. Относительно более простой задачей является расчет величины колебательной суммы по состояниям. Известно, что нелинейная молекула может совершать 3N-6 колебаний, а линейная – 3N-5. Если в молекуле имеется степень свободы, связанная с внутренним вращение, то число колебаний соответственно уменьшится. В общем случае колебательная сумма по состояниям для молекулы с числом колебаний m имеет следующий вид
где
Статистический вариант расчета констант скоростей элементарных химических реакций удобен при проведении практических расчетов. Тем не менее, для анализа полученных данных определенное преимущество имеет термодинамический подход. Используя известные формулы термодинамики, можно константу равновесия образования активированного комплекса выразить через свободную энергию активации Гиббса (
Для мономолекулярных реакций, с которыми мы будем в дальнейшем преимущественно иметь дело, образование активированного комплекса происходит без изменения числа частиц,
По аналогии с уравнением Аррениуса (4.1) предэкспоненциальный множитель А0 можно выразить как
где T – температура, при которой проводится расчет и эксперимент. Для расчета предэкспоненциального множителя
Энтальпия активации, энтропия активации и свободная энергия Гиббса активации рассчитываются соответственно из выражений (4.11)-(4.13)
где Энтальпия активации реакции
где n – молекулярность реакции.
Тепловой эффект (энтальпия) реакции рассчитывается как разница суммы энтальпий образования продуктов и суммы энтальпий образования реагентов реакции по уравнению (4.15)
Основные этапы изучения механизма химической реакции и расчета кинетических и термодинамических параметров будут рассмотрены в Примере 4.1.
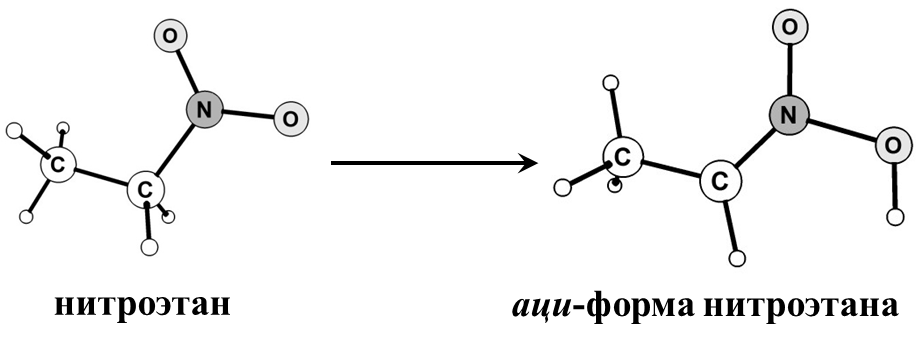
Пример 4.1С использованием программы Gaussian 09W изучить реакцию образования аци-формы нитроэтана. Рассчитать значения энтальпии активации и энтальпии реакции. Построить график зависимости lg(k)=f(1/T) и определить значение lg(A0) при T=700К.
Образования аци-формы нитроалканов – это реакция переноса атома водорода от углерода к атому кислорода нитрогруппы (Рис. 4.5).
Рисунок 4.5 Реакция образования аци-формы нитроэтана
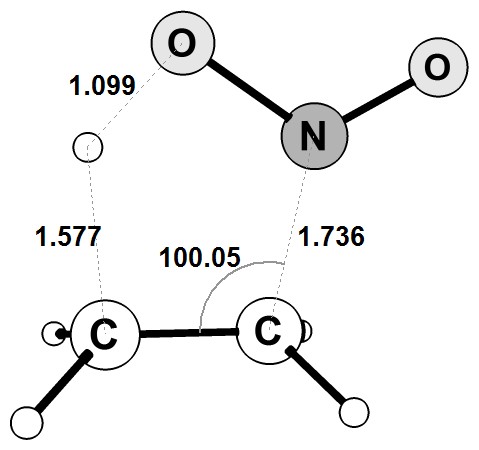
1. На первом этапе необходимо построить и рассчитать геометрию (провести оптимизацию) молекул нитроэтана и аци-формы нитроэтана, соответствующие реагенту и продукту реакции (Рис. 4.5). Для расчета оптимизации применяется следующие параметры: # pm3 opt=(calcfc,maxcycle=200) scf=(xqc,maxcycle=200) freq nosymm 2. Производится построение структуры переходного состояния с последующим расчетом. Переходному состоянию реакции образования аци-формы будет соответствовать структура, в которой разрывается связь С-H и начинает образовываться связь O-H (Рис. 4.6).
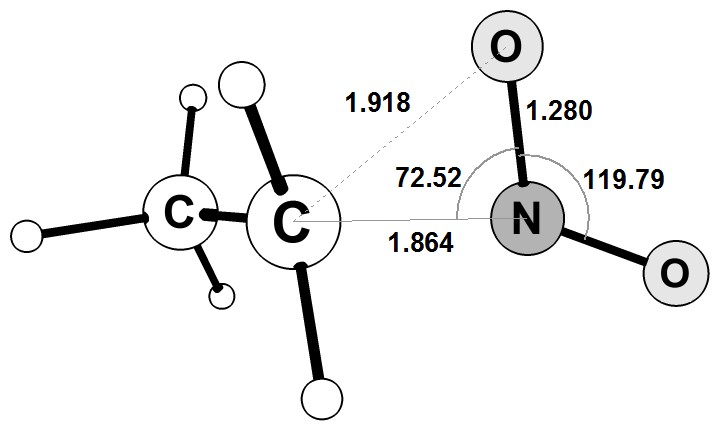
Рисунок 4.6 Структура переходного состояния реакции образования аци-формы нитроэтана
Для построения переходного состояния нужно открыть в программе GaussView out-файл, соответствующий оптимизированной структуре молекулы нитроэтана (реагента). В открытом окне производится непосредственно построение переходного состояния подобное структуре, приведенной на Рис. 4.6. Затем необходимо сохранить файл как TS.gjf. Для расчета переходного состояния необходимо использовать в командной строке входного файла следующие параметры:
# pm3 opt=(ts,calcall,maxcycle=200,noeigentest) scf=(xqc,maxcycle=200) freq nosymm
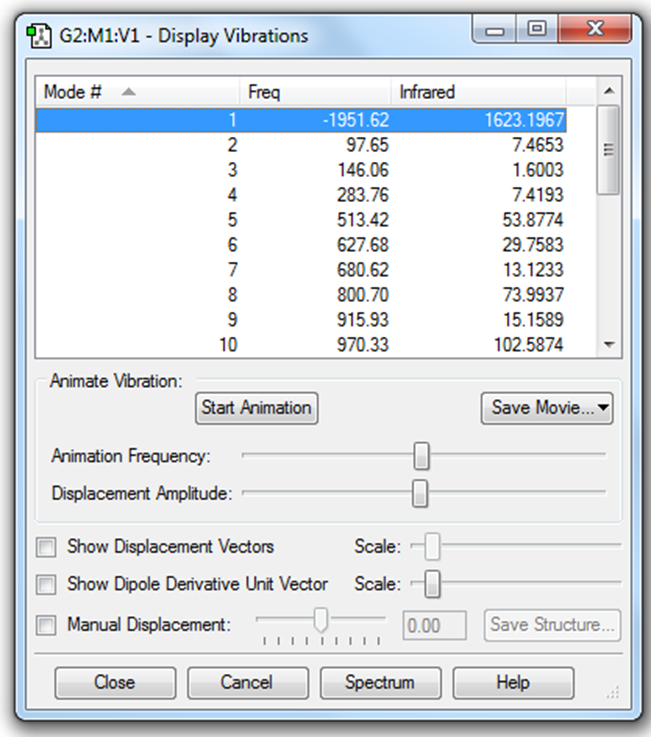
3. Для того чтобы проверить соответствие структуры переходному состоянию, необходимо в программе GaussView открыть файл TS.out, в главном меню программы выбрать Results\Vibrations, как показано на Рис. 2.9. !Примечание Особенность программы GaussView заключается в том, что мнимая частота приводится со знаком минус!
Первая частота для переходного состояния образования аци-формы составляет -1951.62 см-1 как это показано на Рис. 4.6. Данная частота соответствует движению атома водорода от углерода к кислороду!.
Рисунок 4.6 Частоты колебаний, соответствующие переходному состоянию реакции образования аци-формы нитроэтана
4. Проводится расчет спусков по координате реакции.
Для создания входного файла необходимо открыть в программе GaussView файл TS.out и сохранить его как IRC.gjf. Командная строка входного файла спусков по координате реакции выглядит следующим образом
# pm3 irc=(calcfc,maxcycle=100,maxpoints=1000,stepsize=5) scf=(xqc,maxcycle=200) nosymm Для визуализации результатов IRC расчетов нужно в программе GaussView открыть файл IRC.out, в главном меню программы выбрать Results\IRC/Path, как показано на Рис. 4.7.
Первая и последние точки графика соответствуют соответственно реагентам и продуктам реакции. ! Примечание: очень часто программа GaussView меняет на графике IRC местами реагенты и продукты реакции. Точка в максимуме энергии соответствует переходному состоянию реакции !.
Рисунок 4.7 Визуализация кривой спусков по координате реакции в программе GaussView
5. На данном этапе проводится оптимизация первой и последней точек спусков по координате реакции. Для этого на графике, приведенном на Рис. 4.7 нужно выбрать точку соответствующую реагентам реакции и сохранить ее как R.gjf, затем выбрать точку соответствующую продуктам реакции и сохранить ее как P.gjf. Для оптимизации первой и последней точек используются параметры аналогичные тем, что указаны в пункте 1 данного примера.
# pm3 opt=(calcfc,maxcycle=200) scf=(xqc,maxcycle=200) freq nosymm 6. Производится расчет энтальпии активации, энтропии активации, энергии Гиббса активации и энергии активации реакции по формулам (4.11)-(4.14). Энтальпия реакции рассчитывается по уравнению (4.15). Значения энтальпии, энергии Гиббса и энтропии для структур реагентов, продуктов и переходного состояния находятся в соответствии с Рисунком 2.10. 7. В программе Microsoft Excel cтроится график зависимости lg(k)=f(1/T) исходя из выражения (4.9) (Рис. 4.8). Здесь KB = 1.380 × 10-23; Дж/К, h = 6.626 × 10-34 Дж×с; R = 8.314 Дж/(моль×К)
Величина предэкспоненциального множителя lg(A0) определяется на основе выражения (4.10).
Рисунок 4.8 График зависимости lg(k)=f(1/T) для реакции образования аци-формы нитроэтана
Задание 4.1 Определить значения энтальпии активации, определить энтальпию реакции, построить график зависимости lg(k)=f(1/T) и определить значение lg(A0) для следующих реакций:
1) элиминирования азотистой кислоты от молекулы нитроэтана
C2H5NO2 → CH2=СH2 + HNO2
Данная реакция протекает через переходное состояние с плоским пятичленным циклом, структура которого представлена на Рис. 4.9.
Рисунок 4.9 Переходное состояние реакции элиминирования азотистой кислоты от молекулы нитроэтана
2) нитро-нитритной перегруппировки с образованием этилнитрита в качестве продукта.
C2H5NO2 → C2H5ONO
В ходе данной реакции наряду с изменением других параметров реакционного центра происходит поворот нитрогруппы в молекуле нитроэтана и ПС, который сопровождается разрывом связи С-NO2 и образованием связи С-ONO. Структура переходного состояния приведена на Рис. 4.10.
Рисунок 4.10 Переходное состояние реакции нитро-нитритной перегруппировки в молекуле нитроэтана Задание 4.2 Изучить механизм многостадийной реакции элиминирования воды от динитрометана
CH2(NO2)2 → CN2O3 + H2O
Для каждой стадии рассчитать значения энтальпии активации. Построить график зависимости lg(k)=f(1/T) и определить значение lg(A0). Определить энтальпию реакции. Определить какая из трех стадий является лимитирующей.
Реакция элиминирования воды от молекулы динитрометана протекает в три стадии:
1) На первой стадии образуется молекула аци-формы динитрометана (Рис. 4.11), через переходное состояние TS1.
Рисунок 4.11 Схема реакция образования аци-формы динитрометана через переходное состояние TS1 2) На второй стадии происходит конформационный переход, связанный с поворотом ОН группы аци-формы динитрометана на 180° (Рис. 4.12). Переходному состоянию соответствует структура TS2. Значение двугранного угла O-N-O-H cоставляет 101.7°.
Рисунок 4.12 Конформационный переход в аци-форме динитрометана, протекающий через переходное состояние TS2
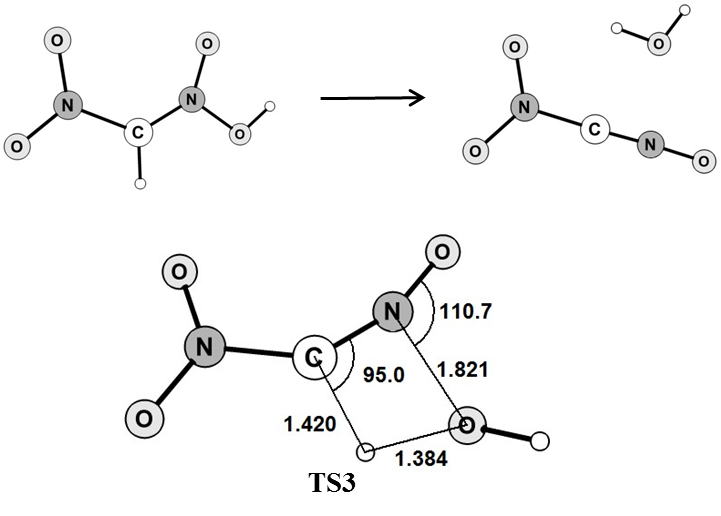
3) На третьей стадии происходит непосредственное отщепление молекулы воды от аци-формы динитрометана (рис. 4.13) через переходное состояние TS3.
Рисунок 4.13 Отщепление воды от аци-формы динитрометана через переходное состояние TS3
Поиск по сайту: |
 (4.2),
(4.2), (4.3),
(4.3),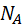 – число Авогадро,
– число Авогадро,  – объем, в котором движется молекула,
– объем, в котором движется молекула,  - энергия активации реакции при 0 К.
- энергия активации реакции при 0 К.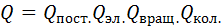 (4.4)
(4.4)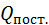 определяется массой молекулы
определяется массой молекулы (4.5),
(4.5),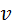 объем, в котором движется молекула.
объем, в котором движется молекула.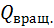 зависит от вида молекулы. Для наиболее простого случая – двухатомной молекулы
зависит от вида молекулы. Для наиболее простого случая – двухатомной молекулы 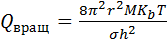 (4.6),
(4.6),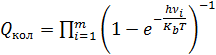 (4.7),
(4.7),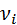 – частота колебания.
– частота колебания. ), а также энтропию активации (
), а также энтропию активации ( 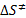 ) и энтальпии активации (
) и энтальпии активации ( 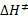 )
)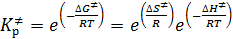 (4.8)
(4.8) , и, следовательно, константу скорости можно представить в виде:
, и, следовательно, константу скорости можно представить в виде: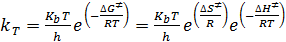 (4.9)
(4.9)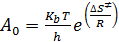 (4.10),
(4.10),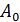 необходимо корректно оценить составляющие энтропии активации, связанные с различными видами движения: колебательными, вращательными (вращения молекулы как целого и внутреннего вращения). Для реакций мономолекулярного распада поступательную составляющую энтропии активации можно не учитывать.
необходимо корректно оценить составляющие энтропии активации, связанные с различными видами движения: колебательными, вращательными (вращения молекулы как целого и внутреннего вращения). Для реакций мономолекулярного распада поступательную составляющую энтропии активации можно не учитывать.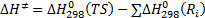 (4.11)
(4.11)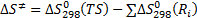 (4.12)
(4.12)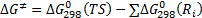 (4.13),
(4.13), ,
, 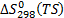 ,
, 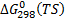 – соответственно энтальпия, энтропия и свободная энергия Гиббса переходного состояния;
– соответственно энтальпия, энтропия и свободная энергия Гиббса переходного состояния;  ,
, 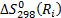 ,
, 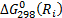 - соответственно энтальпия, энтропия и свободная энергия Гиббса реагентов.
- соответственно энтальпия, энтропия и свободная энергия Гиббса реагентов. (4.11) связана с энергией активации
(4.11) связана с энергией активации 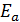 (4.1) уравнением (4.14).
(4.1) уравнением (4.14). (4.14),
(4.14),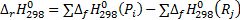 (4.15)
(4.15)