 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Термодинамічний потенціал. Теорема Нернста
Внутрішня енергія Енергія Гальм-Гольца Ентальпія Потенціал Гіббса Теорема Нернста. Третій закон термодинаміки.
Внутрішня енергія Термодинамічні потенціали – визначені функції об’єму, тиску і температури, ентропії та інших макропараметрів, що характеризують стан термодинамічної системи. В кожній комбінації незалежному параметру відповідає свій термодинамічний потенціал. Зміни потенціалу, що відбуваються в ході процесів, визначають роботу, що здійснює тіло, або отриману системою теплоту, або вказує напрям даного процесу. При розгляденні термодинамічного потенціалу, використовують рівняння першого закону термодинаміки у вигляді рівняння:
Так як термодинамічний потенціал є функцією стану системи, то приріст будь-якого потенціалу дорівнює повному диференціалу функції. Повний диференціал функції f(x;y) змінних x і y визначається виразом:
Тому якщо в ході перетворень для приросту величини f отримуємо вираз, що має вигляд: df=x(A;B)dA +y(A;B)dB (2) то можна стверджувати, що величина f - функція змінних А і В, причому функції x(A;B), y(A;B) – частинні похідні функції f(A;B). Тоді:
З першого закону термодинаміки для обернених процесів, зміна внутрішньої енергії dU=TdS-pdV згідно з рівнянням (2) і (3), знаходимо:
Співставляючи (4) і (2), бачимо, що в якості так-званих природних змінних внутрішньої енергії виступають змінні ентронії і об’єму. При відсутності теплообміну з зовнішнім середовищем:
і робота дорівнює зменшенню внутрішньої енергії тіла:
Формула (5) справедлива як при обернених, так і при необернених процесах. При V=const Об’мна теплоємність:
Енергія Гальм-Гольца Згідно рівнянь першого закону термодинаміки
Функція
називається енергією Гальм-Гольца або вільною енергією. Відповідно до (7) і (8), при оберненому ізотермічному процесі робота дорівнює зменшенню енергії Гальм-Гольца:
Зрівнюючи (9) і (5), можна побачити, що при ізотермічних процесах вільна енергія грає таку саму роль, як і внутрішня енергія при адіабатичних поцесах. У випадку необернених ізотермічних процесів:
і робота:
З цього слідує, що зменшення енергії Гальм-Гольца характеризує верхню границю роботи, яку може здійснити система при ізотермічному процесі. Якщо продиференціювати рівняння (8) з урахуванням рівняння першого закону термодинаміки, отримаємо: dF=-SdT-pdV (11) За рівняннями (2) і (3) і на основі (11) знаходимо, що:
З даних двох рівнянь слідує, що природніми змінними енергії Гальм-Гольца є змінні температури і об’єми. Поділимо рівняння першого закону
При умові, що T=const, V=const, отримаємо, що :
З рівняння (14) слідує, що необернений процес, що протікає при постійних температурі і об’ємі супроводжується зниженням енергії Гальм-Гольца і рівновісним при цих умовах є стан з мінімальною енергією Гальм-Гольца.
Ентальпія Для процесів, які протікають при тостійному тискові (p=const), перший закон термодинаміки можна записати у вигляді:
або:
Величина (U+pV) дорівнює H: U+pV=H (15) і це є функція зміни стану, яка називається ентальпією. Використовуючи цю функцію, знаходимо, що кількість теплоти, отриманої тілом в ході ізобарного процесу, чисельно дорівнює:
Якщо продиференціювати рівняння (15) з урахуванням другого закону термодинаміки dH=dU+pdV+Vdp=TdS-pdV+pdV+Vdp=TdS+Vdp Звідси витікає, що ентальпія – термодинамічна функція змінних ентропії і тиску.Її частинні похідні:
З урахуванням (16), теплоємність при p=const:
Співставляючи властивості внутрішньої енергії і ентальпії, неважко зрозуміти, що при p=const ентальпія володіє властивостями, аналогічними до тих, що має внутрішня енегрія при V=vonst.
Потенціал Гіббса Енергією Гіббса називається функція стану, що визначається рівнянням: G=H-TS=U+pV-TS (19) Повний диференціал енергії Гіббса визначається як:
Така як dU=TdS-pdV, то нотенціал енергії Гіббса: dG=Vdp-SdT Тобто природними змінними для функції енергії Гіббса є тиск і температура (p i T), а частинні похідні цієї функції:
Якщо температура T і тиск p залишаються сталими, то відповідно до рівняння (13) можна записати:
З рівняння слідує: якщо необхідний процес буде проходити при посійному тискові p=const і постійній температурі T=const, то це буде супроводжуватися зменшенням енергії Гіббса. В стані рівноваги енергія Гіббса буде мінімальною.
Поиск по сайту: |
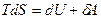
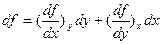 (1)
(1) (3)
(3)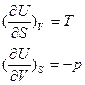 (4)
(4)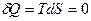
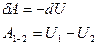 (5)
(5)
 (6)
(6) (7)
(7)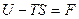 (8)
(8) (9)
(9)
 (10)
(10) (12)
(12) (13)
(13) (14)
(14)

 (16)
(16) , то отримаємо:
, то отримаємо: (17)
(17) (18)
(18)
 (20)
(20)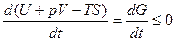 (21)
(21)