 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Перший закон термодинаміки
(закон збереження енергії для систем, в яких основну роль грають теплові процеси) Якщо термодинамічній системі надати зовні деяку кількість теплоти
Робота
З урахуванням цього, рівняння (11) запишемо:
Для нескінченно малої зміни стану системи можна записати:
Дане рівняння – математичний запис першого початку термодинаміки. За першим законом термодинаміки: теплота, надана системі витрачається на зміну внутрішньої енергії системи і на здійснення системою роботи проти зовнішніх сил. Для визначення кругових процесів, коли система набуває ряд змін і повертається у початковий стан (положення):
Тому перший закон термодинаміки:
Це твердження (перший закон термодинаміки) було сформоване Гальм-Гольцем у 1747 році. Якщо система здійснює круговий процес, то повна кількість теплоти, яка надається системі, дорівнює здійсненій в ній роботі. З рівняння (13) випливає, що у випадку кругових процесів:
Перший початок термодинаміки стверджує: неможливий процес, єдиним результатом якого було б виконання роботи без яких-небудь змін в інших тілах. Іншими словами, неможливий вічний двигун першого роду. Усі формулювання першого закону термодинаміки виражають закон збереження енергії. У випадку теплового процесу для однорідних тіл, здатних виконувати роботу при зміні об’єму, запишемо:
Якщо враховувати рівняння (10), запишемо:
Ізопроцеси в ідеальних газах А) Ізотермічний Ізотермічний процес здійснються при сталій температурі системи (Т=const), при m=const, n=const. При pV=const (16)
Ізотермічні процеси відбуваються дисить повільно. При цьому поняття температури не втрачає сенсу. Стискаємість ідеального газу при T=const характеризується ізотермічним коефіцієнтом стискаємості χ, який визначається як відносна зміна об’єму, що зумовлює зміну тиску на одиницю:
де V – початковий об’єм
Знайдемо коефіцієнт χ для ідеального газу. Продиференціювавши (16) при T=const, дістанемо:
звідси:
тобто при
Для реазізації ізотермічного процесу треба забезпечити ідеальний тепловий контакт між газом і термостатом (тілом, що має сталу температуру). Оскільки
Роботу
З урахуванням (20), рівняння (19) перепишемо так:
Б) Ізобарний Ізобарний процес відбувається в системі при сталому тиску (P=const).
Такий процес можна здійснити, коли газ, наприклад, міститься в циліндрі з рухомим поршнем. Зміна температури газу в такому циліндрі зумовлює переміщення порщня, тобто зміну об`єму. Тиск при цьому залишається сталим:
- рівняння ізобарного процесу,виражає закон Гей-Люссака:
Аналогічно, коефіцієнт χ:
Розглянемо графік p(V): газ, поміщений в циліндр із вільно-рухомим поршнем, під час нагрівання Елементарна робота:
є повним диференціалом деякої функції. Оскільки p=const, то робота є однозначною функцією параметрів початкового і кінцевого станів системи (парметр V). Звідси:
Диференціюючи рівняння Менделєєва-Клайперона при сталому тиску, одержимо:
Тоді:
Кількість теплоти, якою газ обмінюється в ізобарному процесі при незалежності
Кількість теплоти
В) Ізохорний Ізохорний процес відбувається при сиалому об’ємі газу (V=const):
- рівняння ізохорного процесу
Аналогічно до коефіцієнту
Зв’язок між коефіцієнтами
Робота в ізохорномк процесі дорівнює нулю:
Тоді рівняння першого закону термодинаміки:
Г) Адіабатичний Адіабатичний процесвідбувається без теплообміну з навколишнім середовищем. Адіабатне розширення або стискання газу можна здійснити, помістивши його в циліндр із нетеплопровідними стінками і поршнем, і досить повільно переміщуючи поршень назовні або всередину циліндра. Стан системи при адіабатичному процесі можна змінити тільки за допомогою зміни зовнішніх парамеирів. Для цього процесу характерним є те, що газ увесь час залишається під зовнішнім тиском, який дорівнює пружності газу. Другою умовою адіабатичного процесу є теплоізольованість газу від навколишнього середовища. Для адіабатичного процесу рівняня першого закону термодинаміки має вигляд:
Виразимо P через V і T з рівняння стану ідеального газу:
Підставимо в попереднє рівняння і скоротимо на відмінний від нуля множник
Розділимо обидві частини рівняння на
Це співвідношення можемо записати у вигляді:
Звідси слідує, що при адіабатичному процесі:
Проінтегрувавши і підставивши, одержимо:
- рівняння адіабатичного газу в змінних T і V:
враховуючи, що величини M,m і R – сталі:
- рівняння адіабатичного ідеального газу в змінних P і V (рівняння Пуассона). При ізотермічному процесі (pV=const), тиск газу зменшується обернено-пропорційно об’єму в першому степені. При адіабатичному розширенні тиск зменшується обернено-пропорційно
Виведемо формули для розрахунку роботи при адіабатичному процесі: з попередніх викладок для 1 моль ідеального газу:
Оскільки
то:
Графічно робота зображена площею заштрихованої трапеції.
Лекція 3
Поиск по сайту: |
 і виконати на цією системою роботу
і виконати на цією системою роботу  зовнішніми силами, то внутрішня енаргія цієї системи зміниться на величину
зовнішніми силами, то внутрішня енаргія цієї системи зміниться на величину  , яка чисельно дорівнює:
, яка чисельно дорівнює: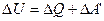 (11)
(11) , яка здійснюється системою проти зовнішніх сил, тобто:
, яка здійснюється системою проти зовнішніх сил, тобто: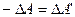
 (12)
(12) (13)
(13)


 (14)
(14) (15)
(15) , рівняння Менделєєва-Клайперона запишемо:
, рівняння Менделєєва-Клайперона запишемо:

 (17)
(17) - зміна об’єму, яка зумовлює зміну тиску на
- зміна об’єму, яка зумовлює зміну тиску на 

 (18)
(18)
 , тоді
, тоді 

 , то перший закон термодинаміки для ізотермічного процесу:
, то перший закон термодинаміки для ізотермічного процесу: визначають:
визначають: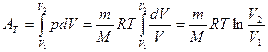 (20)
(20) (21)
(21)


 (22)
(22)
 - коефіцієнт об’ємого розширення газу
- коефіцієнт об’ємого розширення газу

 або під час охолодження
або під час охолодження  здійснює ізобарний процес.
здійснює ізобарний процес. (23)
(23) (24)
(24)
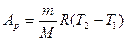
 від температури:
від температури: (25)
(25) йде не тільки на збереження внутрішньої енергії, а йна виконання роботи щодо розширення газу:
йде не тільки на збереження внутрішньої енергії, а йна виконання роботи щодо розширення газу: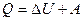 (26)
(26) (27)
(27) За законом Шарля, рівняння ізохорного процесу також можна записувати у вигляді:
За законом Шарля, рівняння ізохорного процесу також можна записувати у вигляді:
 - термічний коефіцієнт тиску (
- термічний коефіцієнт тиску ( 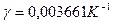 )
)
 :
:
 (28)
(28)
 (29)
(29)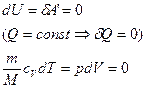 (30)
(30)
 :
:
 :
:


 (31)
(31)
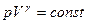 (32)
(32)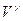 . Хід адіабати крутіший порівняно з ізотермою. Фізично це пояснюється тим, що при адіабатичному розширенні зменшення тиску зумовлене не тільки збільшенням об’єму, а й зменшенням температури.
. Хід адіабати крутіший порівняно з ізотермою. Фізично це пояснюється тим, що при адіабатичному розширенні зменшення тиску зумовлене не тільки збільшенням об’єму, а й зменшенням температури.
 (33)
(33) (34)
(34)
 - показник адіабати
- показник адіабати (35)
(35)