 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Обратная матрица. Матричный метод решения систем линейных уравнений
Алгебраическим дополнением
Пример 1.4.1. Найти алгебраическое дополнение
Δ
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. Любая невырожденная квадратная матрица имеет обратную матрицу
Обратная матрица обладает следующим свойством
Пример 1.4.2. Найти обратную матрицу к матрице А и сделать проверку
Решение: найдем определитель матрицы А
Обратная матрица найдена, сделаем проверку (произведение матриц описано в параграфе 1.1).
Ответ: С помощью обратной матрицы возможно решение систем линейных уравнений. Рассмотрим систему n линейных уравнений c n переменными общего вида
Обозначим матрицы
Тогда систему линейных уравнений (1.4.2) можно записать в виде матричного уравнения
Решение полученного уравнения можно найти, умножив обе части уравнения слева на
Используя свойство
или Такой метод решения систем линейных уравнений получил название матричного методаили метода матричного исчисления. Кроме уравнения (1.4.3) существуют другие матричные уравнения:
и
- решение матричного уравнения (1.4.4). Пример 1.4.3. Решить систему линейных уравнений матричным методом
Решение: обозначим матрицы
По формуле (1.4.1) получим обратную матрицу
и решение матричного уравнения
Ответ: (2,-3,1) □
Задача 1. Найти обратную матрицу
Задача 2. Решить систему линейных уравнений матричным методом
Поиск по сайту: |
 к элементу
к элементу  квадратной матрицы
квадратной матрицы  размерности
размерности  называется произведение числа
называется произведение числа  и определителя, полученного из определителя матрицы
и определителя, полученного из определителя матрицы  и столбца с номером
и столбца с номером  .
. матрицы
матрицы
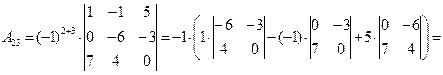 Решение: матрица А имеет размерность 4×4, ее элемент
Решение: матрица А имеет размерность 4×4, ее элемент  . Найдем алгебраическое дополнение
. Найдем алгебраическое дополнение 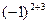 определитель, полученный из определителя матрицы А путем вычеркивания 2-ой строки и 3-его столбца, т.е.
определитель, полученный из определителя матрицы А путем вычеркивания 2-ой строки и 3-его столбца, т.е.
 , которая находится по формуле
, которая находится по формуле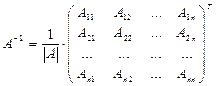 (1.4.1)
(1.4.1) , которое служит для проверки правильности вычисления обратной матрицы (здесь Е – единичная матрица).
, которое служит для проверки правильности вычисления обратной матрицы (здесь Е – единичная матрица).

 .
.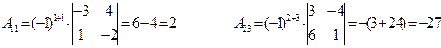 Так как определитель матрицы
Так как определитель матрицы  отличен от нуля, то матрица А является невырожденной, у нее существует обратная матрица
отличен от нуля, то матрица А является невырожденной, у нее существует обратная матрица 

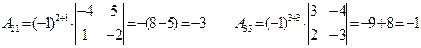

 Тогда обратная матрица согласно формуле (1.4.1) имеет вид
Тогда обратная матрица согласно формуле (1.4.1) имеет вид
 Δ
Δ (1.4.2)
(1.4.2)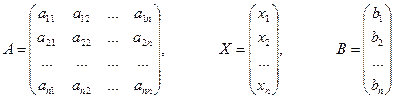
 . (1.4.3)
. (1.4.3)
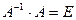 обратной матрицы, получим
обратной матрицы, получим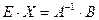
 - решение матричного уравнения (1.4.3).
- решение матричного уравнения (1.4.3).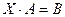 (1.4.4)
(1.4.4) . (1.4.5)
. (1.4.5)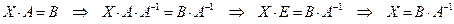 Для решения уравнения (1.4.4) следует умножить уравнение справа на матрицу
Для решения уравнения (1.4.4) следует умножить уравнение справа на матрицу 
 Тогда систему линейных уравнений можно записать в виде
Тогда систему линейных уравнений можно записать в виде 




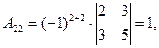

 или
или 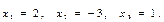


 Задача 3. Решить матричное уравнение
Задача 3. Решить матричное уравнение