 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Матрицы, действия с матрицамиСтр 1 из 10Следующая ⇒
Филиал «Котельники»
Е.Ю. Орлова Линейная алгебра и аналитическая геометрия Учебно-методическое пособие к изучению курса, Практические задания, задания для контрольной и курсовой работы
Котельники ББК 22.147 О-66-4 Рекомендовано к изданию научно-методическим советом филиала «Котельники» университета «Дубна»
Орлова Е.Ю. Линейная алгебра и аналитическая геометрия: Учебно-методическое пособие.-2-е изд., перераб. и доп.-Котельники: Международный университет природы, общества и человека «Дубна», филиал «Котельники», 2011.-74с.
Учебно-методическое пособие к изучению курса линейной алгебры и аналитической геометрии включает в себя план-конспект лекционного материала дисциплины, примеры, иллюстрирующие теоретический материал, задания для самостоятельной работы студентов, а также задания по контрольной и курсовой работе, предназначенные для студентов специальностей «Государственное и муниципальное управление», «Бухгалтерский учет, анализ и аудит», «Финансы и кредит», изучающих применение математических моделей для анализа экономических процессов. Содержание соответствует Государственному образовательному стандарту по дисциплине для перечисленных специальностей очной и заочной формы обучения.
Рецензенты: к.т.н., доцент Кривошеева В.С., зав. кафедрой естественных и гуманитарных наук филиала «Котельники» университета «Дубна», к.т.н., доцент Худякова О.Ю., доцент кафедры математики филиала Угреша» университета «Дубна»
© Е.Ю.Орлова © Международный университет природы, общества и человека «Дубна» филиал «Котельники», 2011 Введение Данное учебно-методическое пособие предназначено для студентов 1 курса экономических специальностей, изучающих курс «Линейная алгебра и аналитическая геометрия» в рамках дисциплины “Математика” всех форм обучения. Оно содержит краткие теоретические сведения разделов “Линейная алгебра” и “Аналитическая геометрия”, примеры решения задач, а также упражнения для самостоятельной работы студентов. В пособии широко представлены задачи экономического анализа, использующие в своем решении математический аппарат соответствующих разделов математики. Для удобства ссылок на теоретические и практические материалы в пособии использована сквозная нумерация глав, параграфов, формул и примеров (например, 1.4 – глава 1, параграф 4, пример 2.3.5 – глава 2, параграф 3, пример № 5). Доказательства теорем и формул опущены с целью сокращения объема пособия. При необходимости, эти сведения могут быть получены из литературы, указанной в конце пособия. Рассматриваемые примеры в пособии ограничиваются символом окончания решения Δ. В конце методического пособия находятся задания для самостоятельной работы студентов заочной формы обучения над контрольной и курсовой работой. Курсовая работа предполагает тщательное изучение матричного исчисления и практическое применение матричных моделей математики для анализа экономических задач и задач управления хозяйственными объектами. Теоретический материал учебного пособия используется при изучении других разделов математики, теории вероятностей, статистики, эконометрики, экономико-математических методов и будет полезен специалистам различного уровня для постановки корректной математической задачи в экономических исследованиях и при ее решении. Глава 1. Линейная алгебра Матрицы, действия с матрицами
размерность матрицы 3×4, элементы матрицы - Главную диагональ матрицы составляют элементы с одинаковыми индексами Матрица называется - квадратной, если число строк n равно числу столбцов m (n=m), - матрицей-строкой, если содержит только одну строку (n=1), - матрицей-столбцом, если содержит только один столбец (m=1), - диагональной, если она квадратная и ненулевыми элементами являются только элементы главной диагонали, - единичной, если она диагональная и элементами главной диагонали являются единицы ( - матрицей треугольного вида, если она квадратная и под ее главной диагональю все элементы – нулевые, - матрицей трапециевидной формы, если она прямоугольная и под ее главной диагональю все элементы – нулевые. Над матрицами можно совершать следующие действия: - сложение матриц, - умножение матриц на число, - транспонирование матриц, - произведение матриц друг на друга. 1. При сложении матрицы A размерности n×m и матрицы B размерности n×m получается матрица C размерности n×m, каждый элемент которой равен сумме соответствующих элементов матриц A и B, т.е. Совпадение размерностей матриц A и B является необходимым условием сложения матриц. Сложение матриц обладает свойством коммутативности, т.е. A+B=B+A. Пример 1.1.1. Даны матрицы A и B. Необходимо найти матрицу C=A+B.
Решение: размерности матриц A и B совпадают и равны 3×2 . Следовательно, складывать их можно, при сложении получится матрица C размерности 3×2 .
2. При умножении матрицы A размерности n×m на произвольное действительное число l получается матрица B размерности n×m, каждый элемент которой равен произведению соответствующего элемента матрицы A и числа l, т.е.
Пример 1.1.2. Дана матрица A. Умножить матрицу на число 6. Решение:
3. При транспонировании матрицы А размерности n×m получается матрица В размерности m×n, каждый элемент которой равен Пример 1.1.3. Дана матрица А. Необходимо ее транспонировать.
Решение: 4. При умножении матрицы А размерности n×m на матрицу В размерности m×k получается матрица С размерности n×k, каждый элемент которой равен сумме парных произведений элементов строки i матрицы А и столбца j матрицы В, т.е.
Необходимым условием умножения матриц друг на друга является равенство числа столбцов первой матрицы и числа строк второй матрицы. Произведение матриц не обладает свойством коммутативности, т.е. в общем случае
Пример 1.1.4. Даны матрицы А и В. Найти произведение АВ.
Решение: число столбцов матрицы А равно двум и совпадает с числом строк матрицы В, поэтому перемножать матрицы А и В можно, в результате получим матрицу С размерности 3×4:
 , ,
где Δ
Действия над матрицами позволяют вычислять матричные выражения.
Пример 1.1.5. Даны матрицы А, В. Найти значение матричного выражения
□
Задача 2. Даны матрицы 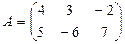 и и  . Найти значение матричного выражения . Найти значение матричного выражения
Любая квадратная матрица обладает числовой характеристикой, которая называется определителем этой матрицы. Определителем второго порядкаматрицы А размерности 2×2 называется число
Пример 1.2.1. Дана матрица Решение:
Определителем третьего порядкаматрицы А размерности 3×3 называется число Пример 1.2.2. Дана матрица Решение:
Определитель четвертого порядка вычисляется через определители третьего порядка по аналогичной формуле. Формула носит название разложения Лапласа и позволяет раскладывать определители любого порядка по элементам любой строки или столбца. Рассмотрим систему n линейных уравнений c n переменными общего вида
Решение данной системы находится по формулам Крамера
а определители Пример 1.2.3. Решить систему линейных уравнений методом Крамера
Ответ: (-1, 3, 2) Δ
Задача 2. Решить системы линейных уравнений методом Крамера:
Рассмотрим систему n линейных уравнений c n переменными общего вида
Расширенной матрицей системыназывается матрица всех ее коэффициентов вида
Две расширенные матрицы называются эквивалентными, если соответствующие им системы линейных уравнений эквивалентны (имеют одинаковое решение). Например, расширенные матрицы
так как соответствующие им системы линейных уравнений
имеют решение Метод Гаусса для решения системы линейных уравнений основан на элементарных преобразованиях расширенной матрицы. В результате каждого из элементарных преобразований расширенная матрица изменяется, однако система линейных уравнений, соответствующая полученной матрице, эквивалентна исходной системе линейных уравнений. Следующие преобразования расширенных матриц называются преобразованиями Жордана-Гауссаи не нарушают их эквивалентность:
Алгоритм метода Гаусса:
Пример 1.3.1. Решить систему линейных уравнений методом Гаусса
Решение: 1. Составим расширенную матрицу данной системы линейных уравнений:
2. Преобразуем полученную матрицу к трапециевидной форме:
1. ней расширенной матрице и решим ее Ответ: (1, 5, 2) Δ Метод Гаусса используется также при решении систем линейных уравнений, в которых количество уравнений не совпадает с количеством переменных. Примечание: если в процессе элементарных преобразований расширенной матрицы получена строка вида
то ее следует удалить из расширенной матрицы и продолжать преобразования далее, если получена строка вида
то решение задачи завершено, а система линейных уравнений несовместна, т.к. соответствующее уравнение
не имеет решений. Система линейных уравнений называется - совместной, если она имеет хотя бы одно решение; - несовместной,если не имеет решений; - определенной,если имеет ровно одно решение; - неопределенной, если имеет множество решений. Решение в этом случае называется общим.
Задача 1. Решить систему линейных уравнений методом Гаусса:
Поиск по сайту: |
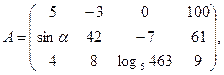
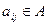 , где i – номер строки, j – номер столбца матрицы A, в котором находится элемент
, где i – номер строки, j – номер столбца матрицы A, в котором находится элемент  .
.
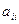 , например, для рассмотренной матрицы элементы
, например, для рассмотренной матрицы элементы  образуют главную диагональ матрицы A.
образуют главную диагональ матрицы A.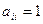 ),
), .
.
 Δ.
Δ.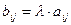 .
.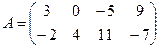
 Δ.
Δ.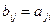 .
.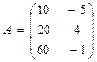
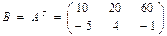 Δ.
Δ.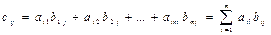 .
. , исключение составляют единичная Е и обратная
, исключение составляют единичная Е и обратная  матрицы, для которых
матрицы, для которых 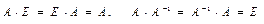 .
.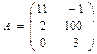 ,
,  .
.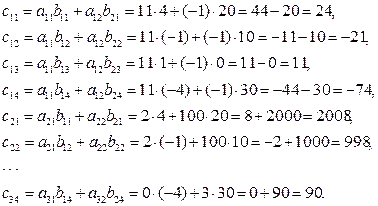

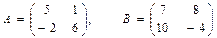
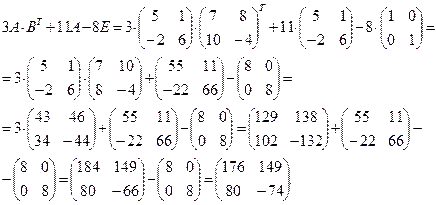
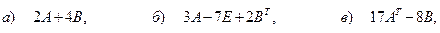
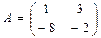 и
и 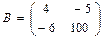 . Найти значение матричного выражения:
. Найти значение матричного выражения: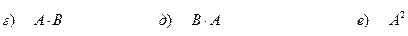




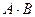 :
:
 (1.2.1)
(1.2.1)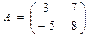 . Найти определитель матрицы А.
. Найти определитель матрицы А.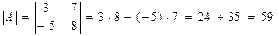 Δ
Δ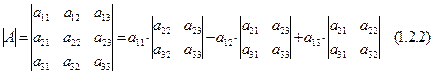
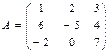 . Найти определитель матрицы А.
. Найти определитель матрицы А.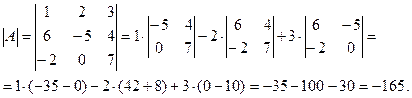
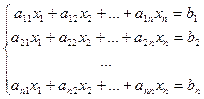
 (если
(если  ), где
), где  - главный определитель системы
- главный определитель системы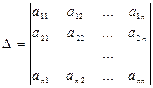 , (1.2.4)
, (1.2.4) получаются из определителя
получаются из определителя 
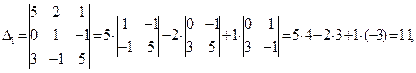
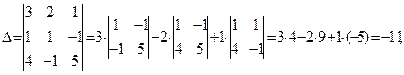 Решение: вычислим определители
Решение: вычислим определители 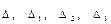 системы и найдем решение по формулам Крамера
системы и найдем решение по формулам Крамера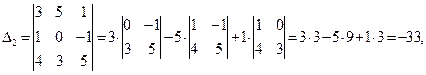 Тогда
Тогда 
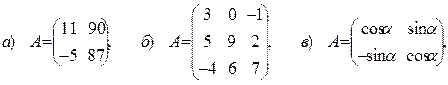 Задача 1. Вычислить определители следующих матриц:
Задача 1. Вычислить определители следующих матриц: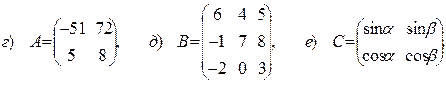

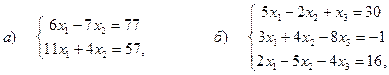
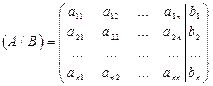 (1.3.2)
(1.3.2) и
и  являются эквивалентными,
являются эквивалентными, и
и 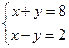
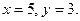
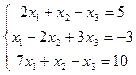

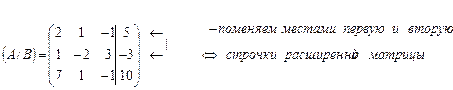
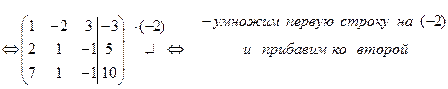
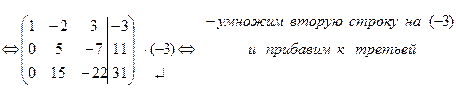





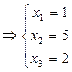
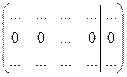 ,
,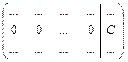 , где
, где  - ненулевое число,
- ненулевое число,
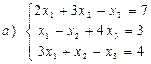



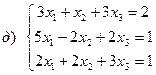
 Задача 2. Решить систему методом Гаусса:
Задача 2. Решить систему методом Гаусса: