 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Динамика материальной точки. Инерциальные системы отсчетаСтр 1 из 12Следующая ⇒
Введение
Физика - это наука о природе, а именно, о строении, взаимодействиях и свойствах составляющих ее тел и полей. Главная задача этой науки – объяснить законы природы, установить причинно-следственные связи. Человек живет в материальном мире. Его окружают физические тела, с ними происходят вполне определенные явления. Естественные науки объясняют их. Знать законы природы необходимо любому культурному человеку. Знания по физике станут начальной базой для изучения специальных предметов. Данное пособие предназначено для студентов – заочников естественнонаучных специальностей, сдающих экзамен и выполняющих контрольные работы по физике. Содержание пособия соответствует разделу общая физика. Пособие составлено в соответствии с государственными образовательными стандартами высшего профессионального образования и охватывает все разделы курса общей физики. Даны так же варианты контрольных работ и рекомендации по их выполнению.
Механика Кинематика частицы (основные понятия кинематики, прямолинейное и криволинейное движение)
Кинематика – это раздел механики, изучающий движение тел без учета взаимодействия, то есть без учета причин, вызывающих это движение. Механическое движение – изменение положения тела относительно других тел с течением времени. Материальная точка – это модель тела, размерами и формой которого можно пренебречь по сравнению с масштабами движения. Тела отсчета – тела, относительно которых определяется или изучается положение данного движущегося тела. Система отсчета – это тело отсчета, связанная с ним система координат и способ измерения времени (часы).
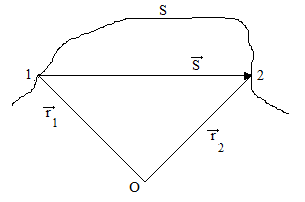
Траектория – линия, которую описывает материальная точка в пространстве при движении. В зависимости от формы траектории движение может прямолинейным и криволинейным. Расстояние, пройденное телом, с момента начала отсчета времени, называется длиной пути. Это длина траектории. Обозначения: длина пути L, S, DS. Вектор, соединяющий начальное положение с последующим положением, называют перемещением. Обозначения перемещения
Введем понятия скорости и ускорения материальной точки. Пусть за промежуток времени Dt материальная точка переместилась из точки 1 в точку 2. Средняя скорость определяет путь, пройденный в единицу времени. Вектор перемещения D
Ускорение – это физическая величина, характеризующая быстроту изменения скорости. Среднее ускорение – это отношение изменения скорости ко времени, за которое это изменение произошло. Вектор среднего ускорения: При использовании декартовой системы координат положение материальной точки задается тремя координатами x, y, z, а при движении точки эти координаты изменяются во времени и, следовательно ее движение описывается тремя уравнениями x(t), y(t), z(t). В этом случае вектор скорости может быть разложен на три взаимно перпендикулярные компоненты: При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения равен пройденному пути, если направление движения не изменяется. 1) В случае равномерного движения:
В проекции на ось ОХ:
2) В случае равнопеременного движения:
В проекции на ось ОХ:
Криволинейное движение – движение, при котором траектория – кривая линия. Рассмотрим один из видов криволинейного движения – движение материальной точки по окружности. 1 случай: равномерное движение по окружности, когда скорость по величине является постоянной
2 случай. Скорость движущейся по окружности материальной точки изменяется по величине и направлению:
Введем векторы угловой скорости и углового ускорения. Вектор угловой скорости При равномерном вращении e = 0 и w = const. Кинематическое уравнение равномерного вращения j = jо+ wt, где jо – начальное угловое перемещение. Угловая скорость тела при равнопеременном вращении w = wо+et. Кинематическое уравнение равнопеременного вращения (e = соnst) j=jо+ wоt+et2/2, где wо – начальная угловая скорость. Динамика материальной точки. Инерциальные системы отсчета
Ый закон Ньютона
Поиск по сайту: |
 ,
,  . Вектор, соединяющий некоторую фиксированную точку пространства с данной движущейся точкой, называется радиус-вектором.
. Вектор, соединяющий некоторую фиксированную точку пространства с данной движущейся точкой, называется радиус-вектором.  Þ
Þ  , перемещение равно изменению радиус-вектора.
, перемещение равно изменению радиус-вектора.
 материальной точки представляет собой приращение радиус-вектора
материальной точки представляет собой приращение радиус-вектора  . Вектор средней скорости
. Вектор средней скорости  cр:
cр:  . Модуль этого вектора определяется как
. Модуль этого вектора определяется как  . Определим вектор скорости материальной точки как предел отношения
. Определим вектор скорости материальной точки как предел отношения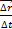 при Dt®0, то есть
при Dt®0, то есть  . Это значит, что вектор скорости материальной точки в данный момент времени равен производной от радиус-вектора
. Это значит, что вектор скорости материальной точки в данный момент времени равен производной от радиус-вектора  .
.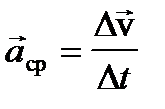 , Переходя к пределу, получим вектор мгновенного ускорения:
, Переходя к пределу, получим вектор мгновенного ускорения:  ; т.е. вектор ускорения материальной точки равен производной от скорости по времени.
; т.е. вектор ускорения материальной точки равен производной от скорости по времени. , причем
, причем  , а вектор ускорения – на компоненты:
, а вектор ускорения – на компоненты: 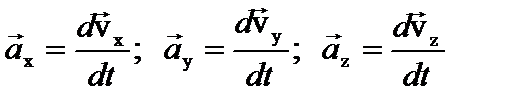 , причем
, причем 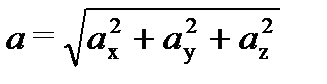 .
.



 , но изменяется по направлению. В этом случае ускорение
, но изменяется по направлению. В этом случае ускорение  или
или  . Нормальное (центростремительное) ускорение характеризует изменение скорости по направлению. Вектор нормального ускорения направлен по радиусу к центру окружности.
. Нормальное (центростремительное) ускорение характеризует изменение скорости по направлению. Вектор нормального ускорения направлен по радиусу к центру окружности.
 . В этом случае полное ускорение состоит из двух составляющих: нормальное ускорение
. В этом случае полное ускорение состоит из двух составляющих: нормальное ускорение  – характеризуется изменением скорости по направлению; тангенциальное ускорение
– характеризуется изменением скорости по направлению; тангенциальное ускорение  характеризуется изменением скорости по величине. Так как компоненты
характеризуется изменением скорости по величине. Так как компоненты 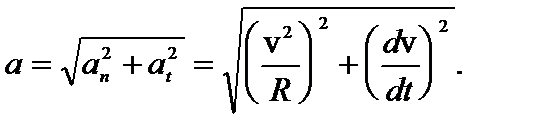
 определяют как:
определяют как:  . Вектор
. Вектор  и представляет собой аксиальный вектор. Изменение вектора
и представляет собой аксиальный вектор. Изменение вектора  , который определяют как
, который определяют как  . Направление вектора
. Направление вектора  – приращением вектора
– приращением вектора