 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
АЛУ для сложения и вычитания чисел с фиксированной запятой
Операция сложения в АЛУ обычно сводится к арифметическому сложению кодов чисел путём применения инверсных кодов - дополнительного или обратного для представления отрицательных чисел. Обратный код имеет два представления нуля (+0, -0), что затрудняет анализ результата операции. Поэтому чаще используется дополнительный код. Алгоритмы выполнения в АЛУ арифметических операций зависят от того, в каком виде хранятся в памяти ЭВМ отрицательные числа - в прямом или дополнительном. В последнем случае сокращается время выполнения операции за счёт исключения преобразования получаемого в АЛУ дополнительного кода отрицательного результата в прямой код, при этом несколько усложняется операция умножения. Алгоритм сложения двоичных чисел с фиксированной запятой, при использовании дополнительного кода для представления отрицательных чисел, заключается в следующем. Производится сложение двоичных кодов, включая разряды знаков. Если при этом возникает перенос из знакового разряда суммы при отсутствии переноса в этот разряд, или возникает перенос в знаковый разряд при отсутствии переноса из разряда знака, то происходит переполнение разрядной сетки. Такой результат получается как при отрицательной, так и положительной суммах. Если нет переносов из знакового и в знаковый разряд суммы или есть оба эти переноса, то переполнения нет. Если получен 0 в знаковом разряде, то сумма положительна и представлена в прямом коде. Если получена 1 в знаковом разряде, то сумма отрицательна и представлена в дополнительном коде. На рис. 4.4 представлена упрощённая структурная схема
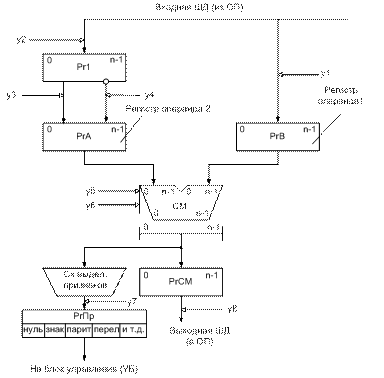
Рисунок 4.4- Структура АЛУ для операций сложения и вычитания АЛУ для операций сложения и вычитания n-разрядных (нулевой разряд знаковый) двоичных чисел с фиксированной запятой. Предполагается, что отрицательные числа хранятся в памяти в дополнительном коде.
В состав АЛУ входят n-разрядный параллельный комбинационный сумматор См, регистр сумматора РгСМ, входные регистры сумматора РгA и РгB, входной регистр АЛУ Рг1. Операнды читаются из оперативной памяти и поступают в АЛУ по входной ШД (в дальнейшем- ШВХ). Для рассматриваемой структуры АЛУ положительные числа должны быть представлены прямым кодом, а отрицательные - дополнительным. Первый операнд размещается в РгB (первое слагаемое или уменьшаемое), а второй в РгА (второе слагаемое или вычитаемое); Рг1 связан с РгA цепями прямой и инверсной передачи кода. Прямая передача используется при операции сложения, а инверсная - при операции вычитания. Результат операции выдается из АЛУ в оперативную память по выходной ШД (в дальнейшем- ШВЫХ). При выполнении операции в АЛУ помимо результата операции формируется код признака результата ПР, который, например, может принимать следующие значения :
Примем, что код признака результата формируется комбинационной схемой выделения признаков СхПр, на входы которой поступают сигналы, соответствующие значениям всех разрядов сумматора, а также сигналы переносов из знакового разряда ПнСм[0] и в знаковый из старшего цифрового разряда ПнСм [1]. Признак переполнения (ПР=11) формируется, если булева функция ПнСм[0]ПнСм[1]vПнСм[0]ПнСм[1]=1. Признак нулевого значения результата (ПР=00)формируется если
Условия выработки признаков положительного и отрицательного результатов имеют соответственно вид: См[0](ПнСм[0]ПнСм[1]vПнСм[0]ПнСм[1]); См[0](ПнСм[0]ПнСм[1]vПнСм[0]ПнСм[1]). При выполнении операции сложения поступившие в АЛУ коды операндов находятся во входных регистрах РгВ и РгА сумматора. Код суммы формируется на выходах схемы СМ и фиксируется в регистре сумматора РгСм. Операция вычитания операнда Y из операнда X Z=X-Y=X+(-Y) сводится к изменению знака вычитаемого Y и последующим применением операции сложения к операндам X и (-У). Изменению знака соответствует следующая процедура: принятый в Рг1 код числа передается в РгA по цепи инверсной передачи кода (линия с кружком на рисунке 4.4), а при сложении осуществляется подсуммирование 1 в младший разряд сумматора. Передачи информации в регистрах АЛУ производятся отдельными микрооперациями, инициируемыми показанными на рис. 4.3.2 управляющими сигналами yi. Например, слово из Рг1 в РгА может быть передано в прямом (управляющий сигнал y3) или в инверсном (управляющий сигнал y4) кодах. Пусть для рассматриваемого АЛУ имеется набор следующих микроопераций: y1: Pr B := ШВХ; прием 1-го операнда в Рг В с входной ШД. y2: Pr 1 := ШВХ; прием 2-го операнда в Рг 1 с входной ШД. y3: Pr A := Pr 1; прямая передача 2-го операнда из Рг1 в РгА. y4: y5: CM := CM+1; y6: Pr CM := CM; передача результата из сумматора в Рг СМ. y7: РгПр := Cx.Пр.; регистру признаков присвоить значение признака результата. y8: ШВЫХ := Pr CM; передача результата из РгСМ на выходную ШД. Ниже приведены описания микропрограмм сложения и вычитания на языке регистровых передач, причем микрооперация y7 состоит в выдаче в регистр признаков (находится в управляющем устройстве) кода признака и в формировании запроса прерывания при переполнении разрядной сетки. Микропрограмма сложения : y1: Pr B := ШВХ; прием 1-го операнда в Pr B. y2: Pr 1 := ШВХ; прием 2-го операнда в Pr 1. y3: Pr A:= Pr 1; прямая передача 2-го операнда в РгА. y6: Pr См:= Pr A + Pr B. y7: РгПр:=СхПр; регистру признаков присваивается значение полученного признака результата, причем если Пр = 11, то прерывание программы по переполнению, иначе y8: ШВЫХ := Pr См. Микропрограмма вычитания : y1: Pr B := ШВХ y2: Pr 1 := ШВХ y4: y5: Pr См := Pr A + Pr B +1 y7: РгПр:=СхПр Если Пр = 11, то прерывание программы по переполнению, иначе y8: ШВЫХ := Pr См
4.3.3 АЛУ для умножения двоичных чисел
В ЭВМ операция умножения чисел с фиксированной запятой сводится к последовательности операций сложения и сдвига. Произведение двух (n- 1)- разрядных чисел может иметь до 2 (n - 1) значащих разрядов, поэтому для выполнения операции умножения целых чисел в АЛУ необходимо предусмотреть возможность формирования произведения, имеющего двойную, по сравнению с сомножителями, длину. В ЭВМ, в которых числа с фиксированной запятой являются дробями, младшие n- 1 разрядов произведения часто отбрасываются, при этом при отбрасывании может производиться операция округления произведения. Для выполнения умножения АЛУ должно содержать регистры множимого, множителя и сумматор частичных произведений, в котором путем соответствующей организации передач производится последовательное суммирование частичных произведений. Операция умножения состоит из n циклов, где n- число цифровых разрядов множителя. В каждом цикле анализируется очередная цифра множителя, и если она равна 1, то к сумме частичных произведений прибавляется множимое, в противном случае прибавление не происходит. Цикл завершается сдвигом множимого относительно суммы частичных произведений либо сдвигом суммы частичных произведений относительно неподвижного множимого. В зависимости от способа формирования суммы частичных произведений различают четыре основных метода выполнения умножения и соответственно четыре структуры АЛУ для этой операции. 1. Умножение, начиная с младших разрядов множителя, со сдвигом суммы частичных произведений вправо и при неподвижном множимом (см. рисунок 4.5).
Рисунок 4.5 - Метод умножения, начиная с младших разрядов множителя со сдвигом суммы частичных произведений вправо
Регистр множителя и сумматор частичных произведений при этом должны иметь цепи сдвига вправо. Регистр множимого может не иметь цепей сдвига. Последовательность действий в каждом цикле выполнения умножения определяется младшим разрядом регистра множителя, куда последовательно одна за другой поступают цифры множителя. Поскольку по мере сдвига множителя вправо старшие разряды регистра множителя освобождаются, он может быть использован для хранения младших разрядов произведения, поступающих из младшего разряда сумматора частичных произведений по мере выполнения умножения. Для этого при выполнении сдвига младший разряд регистра сумматора частичных произведений соединяется со старшим разрядом регистра множителя. После выполнения умножения старшие разряды произведения находятся в регистре сумматора, младшие — в регистре множителя. При данном методе умножения все три регистра имеют одинаковую длину, равную числу разрядов сомножителей. Этот метод умножения нашел наибольшее применение в ЭВМ. 2. Умножение, начиная с младших разрядов множителя, при сдвиге множимого влево и неподвижной сумме частичных произведений (см. рисунок 4.6). Регистр множителя при этом должен иметь цепи сдвига вправо, регистр множимого — цепи сдвига влево, а сумматор частичных произведений не содержит цепей сдвига. Последовательность действий определяется, как и в первом варианте, младшим разрядом регистра множителя. При этом методе регистр множимого и сумматор частичных произведений должны иметь двойную длину. Этот метод требует больше оборудования, но никаких преимуществ не дает, и поэтому применение его нецелесообразно.
Рисунок 4.6 - Метод умножения, начиная с младших разрядов множителя, при сдвиге множимого влево
3. Умножение, начиная со старших разрядов множителя, при сдвиге суммы частичных произведений влево и неподвижном множимом (см. рисунок 4.7).
Рисунок 4.7 - Метод умножения, начиная со старших разрядов множителя при сдвиге суммы частичных произведений влево Регистр множителя и сумматор частичных произведений должны иметь цепи сдвига влево. Регистр множимого не имеет цепей сдвига. Последовательность действий в каждом цикле выполнения умножения определяется старшим разрядом регистра множителя. При использовании этого метода сумматор частичных произведений должен иметь двойную длину. Данный метод требует дополнительного по сравнению с первым методом оборудования. Несмотря на это, он применяется в некоторых АЛУ, так как позволяет без дополнительных цепей сдвига выполнять и деление. Для выполнения операций деления в АЛУ, реализующем первый метод умножения, необходимы дополнительные цепи сдвига влево в регистре множимого (частного) и в сумматоре частичных произведений (разностей). Умножение, начиная со старших разрядов множителя, при сдвиге вправо множимого и неподвижной сумме частичных произведений (см. рисунок 4.8).
Регистр множителя должен иметь цепи сдвига влево, регистр множимого - цепи сдвига вправо. Сумматор частичных произведений не имеет цепей сдвига. Последовательность действий на каждом шаге умножения определяется старшим разрядом регистра множителя. При этом методе умножения и регистр множимого, и сумматор частичных произведений должны иметь двойную длину. Однако, как и третий метод, он не требует дополнительных цепей сдвига для выполнения деления. При четвертом методе, в котором сумма частичных произведений неподвижна, можно совмещать во времени операции сдвига и сложения и за этот счет увеличить быстродействие АЛУ при выполнении умножения (а также деления). Если необходимо образование произведения двойной длины, например, при операциях с целыми числами, наиболее экономичным является первый из рассмотренных методов умножения, так как он позволяет использовать все регистры одинарной длины. Если в результате умножения достаточно иметь произведение одинарной длины, то целесообразно использовать либо первый, либо четвертый метод умножения. При использовании первого метода требуется введение дополнительных цепей сдвига для реализации деления, а при использовании четвертого метода необходимо удлинение сумматора. Выбор одного из этих методов умножения определяется соотношением затрат оборудования на реализацию цепей сдвига и дополнительных разрядов сумматора. При образовании произведений одинарной длины простое отбрасывание младших разрядов вносит погрешность, которая будет накапливаться, так как произведение будет всегда вычисляться с недостатком. Поэтому для повышения точности вычислений часто производят округление результата умножения, вследствие чего погрешность становится знакопеременной. Для округления произведения длина сумматора частичных произведений обычно увеличивается на один разряд. После образования произведения к этому дополнительному разряду прибавляется 1. Если дополнительный разряд произведения был равен 0, то произведение в основных разрядах сумматора получается с недостатком. Если дополнительный разряд был равен 1, то в результате переноса 1 из дополнительного разряда к основным разрядам сумматора добавляется единица и произведение получается с избытком, при этом максимальное значение погрешности произведения равно половине 1 младшего разряда. Следует отметить, что при любом методе умножения операция обычно начинается с анализа на 0 сомножителей. При равенстве нулю хотя бы одного сомножителя умножение не производится, а произведению присваивается нулевое значение. Рассмотрим алгоритм наиболее распространенного метода умножения целых чисел, начиная с младших разрядов, со сдвигом суммы частичных произведений вправо. 1. Берутся модули от сомножителей (числа представляются без знака). 2. Исходное значение суммы частичных произведений принимается равным 0. 3. Если анализируемая цифра множителя равна 1, то к сумме частичных произведений прибавляется множимое; если эта цифра равна 0, прибавление не производится. 4. Производится сдвиг суммы частичных произведений вправо на один разряд. 5. Пункты 3 и 4 последовательно выполняются для всех цифровых разрядов множителя, начиная с младшего. 6. Произведению присваивается знак плюс, если знаки сомножителей одинаковы, в противном случае — знак минус. Деление в ЭВМ обычно сводится к выполнению последовательности вычитаний делителя сначала из делимого, а затем из образующихся в процессе деления частичных остатков, и сдвига частичных остатков.
Поиск по сайту: |
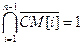 .
.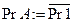 ; инверсная передача 2-го операнда из Рг1 в РгА.
; инверсная передача 2-го операнда из Рг1 в РгА.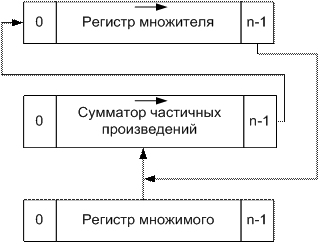
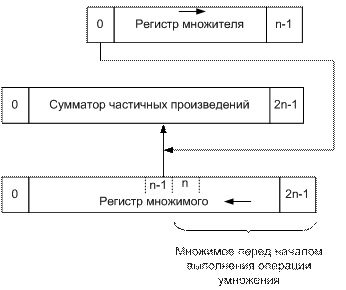
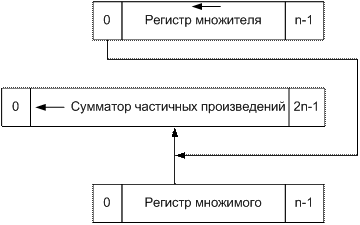
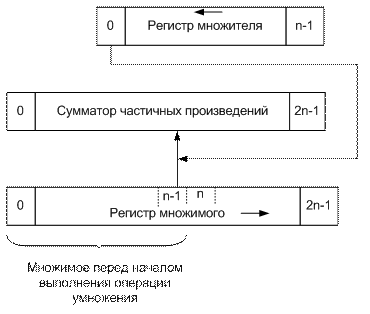 Рисунок 4.8 - Метод умножения, начиная со старших разрядов множителя при сдвиге множимого вправо
Рисунок 4.8 - Метод умножения, начиная со старших разрядов множителя при сдвиге множимого вправо