 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Диференціальні рівняння вищих порядків
Розглянемо д. р.
Для нього теж має місце теорема про існування та єдиність розв’язку, аналогічна сформульованій в п. 2 для першого порядку. Теорема.Якщо в рівнянні
функція
то існує і притому єдиний розв’язок
Умови (2) називаються початковими умовами, де Для диференціального рівняння другого порядку
ці початкові умови мають вигляд:
Задача Коші для д. р. Означення 1. Загальним розв’язком д. р.
яка залежить від 1) вона є розв’язком д. р. (1) для довільних значень 2) для довільних початкових умов Означення 2. Всяка функція, яка може бути отримана із загального розв’язку даного д. р. при конкретних значеннях Якщо функція, яка є загальним розв’язком д. р., отримана у неявній формі
то її називають загальним інтегралом д. р. Процес знаходження загального розв’язку або загального інтеграла даного д. р. називається інтегруванням або розв’язанням диференціального рівняння.
Диференціювальні рівняння другого порядку, які допускають зниження порядку І. Рівняння вигляду
яке не містить явно Наприклад,
Аналогічно,
ІІ. Рівняння другого порядку, яке не містить невідомої функції
За допомогою підстановки
ІІІ. Рівняння другого порядку, яке явно не містить незалежної змінної
За допомогою підстановки
Приклади. 1. Знайти загальний розв’язок д. р.
Розв’язання. Підстановка
Розв’яжемо його заміною
2. Знайти загальний розв’язок рівняння
Розв’язання. Д. р. явно не містить
Приклади. Знайти загальні інтеграли (загальні розв’язки) рівнянь.
Поиск по сайту: |
 - го порядку, записане в явній формі
- го порядку, записане в явній формі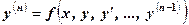 . (1)
. (1)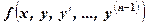 і її частинні похідні по аргументах
і її частинні похідні по аргументах  неперервні в деякій області, що містить значення
неперервні в деякій області, що містить значення ,
, д. р. (1), який задовольняє початковим умовам.
д. р. (1), який задовольняє початковим умовам. (2)
(2) - задані числа.
- задані числа. (3)
(3) (4)
(4) ,
, і така, що задовольняє такі умови:
і така, що задовольняє такі умови: , що функція
, що функція  буде задовольняти ці початкові умови.
буде задовольняти ці початкові умови.
 ,
, ,
,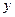 і
і  , розв’язується двохкратним інтегруванням.
, розв’язується двохкратним інтегруванням.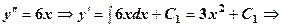
 .
. .
.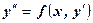
 , де
, де  - невідома функція, (звідки
- невідома функція, (звідки  ) неретворюється в д. р. першого порядку
) неретворюється в д. р. першого порядку .
. ,
,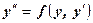
 (звідки
(звідки  ) теж зводиться до першого порядку
) теж зводиться до першого порядку .
. .
. приводить до лінійного д. р. першого порядку
приводить до лінійного д. р. першого порядку .
. ,
,  , маємо
, маємо ,
,

 .
. .
.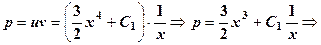
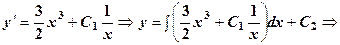
 - загальний розв’язок.
- загальний розв’язок. .
. . Рівняння запишеться:
. Рівняння запишеться:
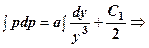
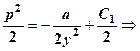
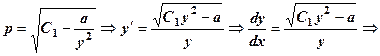
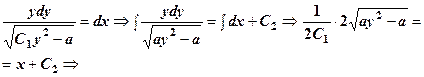
 - загальний інтеграл.
- загальний інтеграл. .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
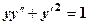 .
.