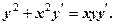|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Д. р. з відокремлюваними змінними
Означення.Д. р.
так, що один із співмножників залежить тільки від х, а другий – тільки від у. При розв’язанні можна дотримуватись такої послідовності. 1. Розкладаємо функцію на множники
2. Замінюємо відношенням диференціалів
3. Розділимо (відокремлемо) змінні так, щоб при dyбув вираз відносно y, а при dx – вираз відносно x, тобто
4. Інтегруємо кожну з частин по відповідним змінним
Якщо позначити відповідні первісні через
Якщо із останньої рівності знайдемо y в явній формі Аналогічним чином означається як д. р. з відокремлюваними змінними рівняння записане в диференціалах:
Д. р. (1) буде з відокремлюваними змінними, якщо кожну з функцій можна розкласти на множники: Похідну замінимо відношенням
Інтегруючи почленно, маємо
Приклади. 1. Розв’язати рівняння Розв’язання.
2. Розв’язання.
3. Знайти частинний розв’язок д. р.
при початковій умові Розв’язання.
Згідно з початковою умовою при х=0 маємо
тоді
отримали частинний розв’язок. Розв’язати самостійно д. р. 1. 2. 3. 4. 5. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16.
Однорідні диференціальні рівняння Означення. Функція
Приклади. Встановити, які з функцій однорідні:
Розв’язання. а)
б) в) г) д) Зауваження. Якщо функція
то її можна звести до вигляду Дійсно, взявши
Наприклад, для
Тепер у виразі даної функції відношення Вправи.а)Представити однорідні функції нульового порядкутак,щоб вони були залежними відносно
Відповіді.
б)Перетворити д.р. так, щоб вони містили вирази
Відповіді.
Означення. Д. р.
Метод розв’язання. 1. Робимо заміну: 2. Переходимо до нової змінної в д. р.
Отримали д. р. з відокремлюваними змінними. 3. Відокремлюємо змінні
4. Інтегруємо: Нехай
загальний інтеграл. 5. Звільняємось від змінної
загальний інтеграл. Приклади. Розв’язати рівняння. 1. Розв’язання. Розділяємо обидві частини рівняння на х:
1) Заміна 2) 3) 4)
2. Розв’язання. Розділяємо обидві частини рівняння на х: 1) 2) 3) 4)
Розв’язати самостійно 1. 3. 5. 7. 9. 11. 12. 13.
Поиск по сайту: |
 називається з відокремлюваними змінними, якщо можна розкласти на множники функцію
називається з відокремлюваними змінними, якщо можна розкласти на множники функцію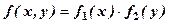
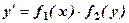
 , тоді дістанемо
, тоді дістанемо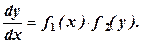
 (
(  ).
).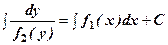 .
. і
і  , то отримаємо загальний інтеграл
, то отримаємо загальний інтеграл .
. , то отримаємо загальний розв’язок.
, то отримаємо загальний розв’язок.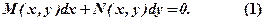
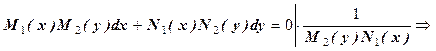
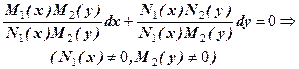
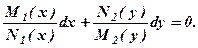
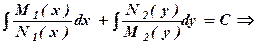
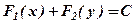 - загальний інтеграл, де
- загальний інтеграл, де 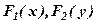 - відповідні первісні.
- відповідні первісні. .
.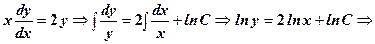


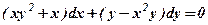
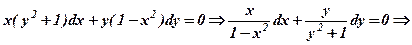
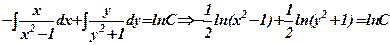


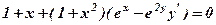
 .
.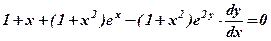
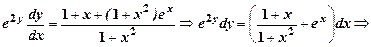
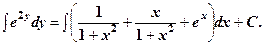
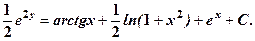
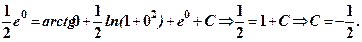
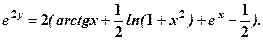
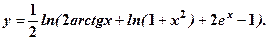
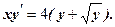
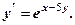
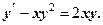
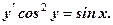
 6.
6. 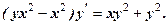
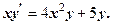
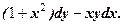
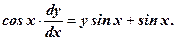

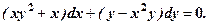
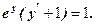
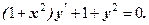
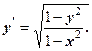
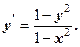
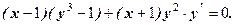
 називається однорідною к-того порядку відносно змінних x і y, якщо для довільного
називається однорідною к-того порядку відносно змінних x і y, якщо для довільного  виконується рівність
виконується рівність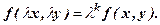

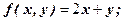


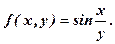
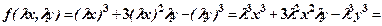
 - однорідна третього порядку.
- однорідна третього порядку. - однорідна першого порядку.
- однорідна першого порядку. - однорідна нульового порядку.
- однорідна нульового порядку.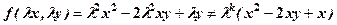 - функція не є однорідною при жодному k.
- функція не є однорідною при жодному k. - однорідна нульового порядку.
- однорідна нульового порядку.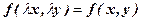 ,
, .
. в останній рівності, отримаємо
в останній рівності, отримаємо ,
,  .
. , якщо чисельник і знаменник почленно розділити на
, якщо чисельник і знаменник почленно розділити на  , то отримаємо
, то отримаємо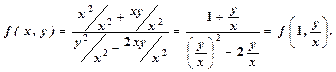
 виступає, як одна змінна.
виступає, як одна змінна. .
.



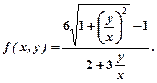






 .
.
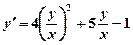 .
.
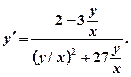


 називається однорідним відносно змінних x iy, якщо функція
називається однорідним відносно змінних x iy, якщо функція 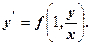
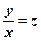 (z – невідома функція) , тоді
(z – невідома функція) , тоді 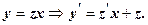
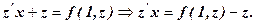
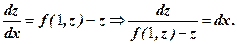
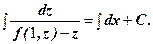
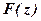 - первісна для лівої частини, тоді
- первісна для лівої частини, тоді -
- , отримаємо
, отримаємо -
-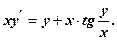
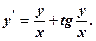
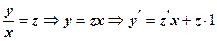 .
.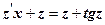
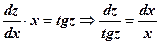
 ,
,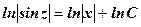
 .
. .
. .
. .
.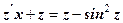 .
.
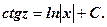
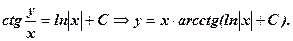
 2.
2. 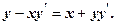
 4.
4. 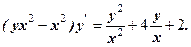
 6.
6. 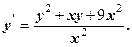
 8.
8. 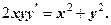
 10.
10. 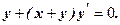
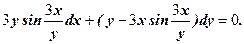
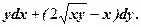
 14.
14.