 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Д. р. першого порядку в неявній формі має виглядСтр 1 из 5Следующая ⇒
Загальні поняття Означення. Рівняння, що містить аргумент, невідому функцію та її похідні або диференціали, називається диференціальним рівнянням (д. р.). В загальному вигляді д. р. може бути записане у формі
яку ще називають неявною формою. Означення. Найвищий порядок похідної або диференціала, що входить в д. р., називають порядкомцього диференціального рівняння. Наприклад,
Якщо ж д. р. (1) можна розв’язати відносно старшої похідної, то отримаємо явну форму д. р.
Означення. Функція Приклади 1.
Цей розв’язок містить довільну сталу С. Надаючи сталій С різних значень, ми отримаємо сім’ю кривих (парабол, див рис. 3.1).
2. Розв’язком д. р. Дійсно, знайдемо спочатку першу похідну 3. Розв’язком д. р.
де Перевіримо. Знайдемо
4. По аналогії з прикладом 1 знайдемо розв’язок д. р.
Після інтегрування маємо
Після повторного інтегрування знаходимо
Задачу про знаходження розв’язку д. р. називають задачею інтегрування даного диференціального рівняння. Графік розв’язку д. р. називається інтегральною кривою. З наведених прикладів бачимо, що розв’язок д. р. знаходиться неоднозначно, геометрично розв’язок д. р. може задавати сім’ю кривих на площині
Диференціальні рівняння першого порядку. Теорема про існування та єдиність розв’язку д. р. Задача Коші Д. р. першого порядку в неявній формі має вигляд
Якщо ж із співвідношення (1) можна виразити
Важливою в теорії д. р. є така теорема. Теорема. ( про існування та єдиність розв’язку д. р.). Якщо в д. р. Означення. Умова Задача знаходження розв’язку Приклад. Розв’язати задачу Коші для д. р. Розв’язання. Шляхом інтегрування знаходимо так званий загальний розв’язок
Отже розв’язком задачі є функція Означення. Загальним розв’язком диференціального рівняння 1) для довільного значення сталої С функція 2) для довільних початкових умов існує таке значення С0, що Означення. Частинним розв’язком диференціального рівняння Тепер можна геометрично пояснити зміст теореми про існування та єдиність розв’язку диференціального рівняння: через кожну точку
Розглянемо диференціальне рівняння Розв’язати диференціальне рівняння Далі перейдемо до вивчення простіших диференціальних рівнянь першого порядку. До них відносяться: 1) диференціальні рівняння з відокремлюваними змінними; 2) однорідні відносно змінних диференціального рівняння; 3) лінійні диференціальні рівняння.
Поиск по сайту: |
 , (1)
, (1) - д. р. першого порядку,
- д. р. першого порядку, - д. р. другого порядку,
- д. р. другого порядку,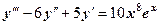 - д. р. третього порядку.
- д. р. третього порядку. (2)
(2)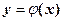 , яка має на деякому інтервалі
, яка має на деякому інтервалі  похідні
похідні  , і яка після підстановки разом з похідними до д. р. (1) або (2) перетворює його в тотожність називається розв’язком д. р. При цьому ще говорять, що функція
, і яка після підстановки разом з похідними до д. р. (1) або (2) перетворює його в тотожність називається розв’язком д. р. При цьому ще говорять, що функція  задовольняє даному д.р.
задовольняє даному д.р. - це д. р. першого порядку. Його розв’язок можна знайти шляхом інтегрування
- це д. р. першого порядку. Його розв’язок можна знайти шляхом інтегрування

 є функція
є функція  .
.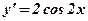 , а тоді другу -
, а тоді другу - 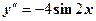 . Підставимо в д. р. вирази
. Підставимо в д. р. вирази  і
і  , отримаємо тотожність
, отримаємо тотожність  .
. ,
,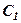 і
і  довільні сталі величини.
довільні сталі величини. ,
,  . Підставимо
. Підставимо  .
.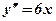 .
.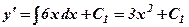 ,
, .
. , як це видно з прикладу 1, де розв’язок залежить від однієї сталої величини С, це для д. р. першого порядку. З прикладів 3 і 4 бачимо, що розв’язки д. р. другого порядку можуть мати дві довільні сталі
, як це видно з прикладу 1, де розв’язок залежить від однієї сталої величини С, це для д. р. першого порядку. З прикладів 3 і 4 бачимо, що розв’язки д. р. другого порядку можуть мати дві довільні сталі  .
. . (1)
. (1) , то отримаємо д. р. першого порядку в явній формі
, то отримаємо д. р. першого порядку в явній формі . (2)
. (2) та її частинна похідна
та її частинна похідна  неперервні в області D, яка містить точку
неперервні в області D, яка містить точку  , то існує єдиний розв’язок д. р.
, то існує єдиний розв’язок д. р.  , який задовольняє умову
, який задовольняє умову  для довільної точки
для довільної точки 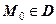 .
. , якій задовольняє розв’язок д. р.
, якій задовольняє розв’язок д. р.  , називають початковою умовою.
, називають початковою умовою. при початковій умові
при початковій умові  .
. , який описує сім’ю парабол. Згідно початкової умови маємо
, який описує сім’ю парабол. Згідно початкової умови маємо .
. - це одна із сім’ї парабол, що проходить через точку М0 (1,-1). Отриманий розв’язок
- це одна із сім’ї парабол, що проходить через точку М0 (1,-1). Отриманий розв’язок  називається функція
називається функція 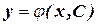 , яка залежить від сталої С і задовольняє умові:
, яка залежить від сталої С і задовольняє умові: є розв’язком диференціального рівняння;
є розв’язком диференціального рівняння; .
.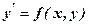 називається розв’язок, який дістають із загального при заданій початковій умові.
називається розв’язок, який дістають із загального при заданій початковій умові. області
області  проходить одна і тільки одна інтегральна крива (див. рис. 3.2).
проходить одна і тільки одна інтегральна крива (див. рис. 3.2).
 в точці
в точці  , отримаємо
, отримаємо  . За геометричним змістом значення похідної в точці М0 співпадає з кутовим коефіцієнтом дотичної до кривої
. За геометричним змістом значення похідної в точці М0 співпадає з кутовим коефіцієнтом дотичної до кривої  , де
, де  - кут нахилу дотичної до осі ОХ). Отже, обчислюючи значення похідної
- кут нахилу дотичної до осі ОХ). Отже, обчислюючи значення похідної  в кожній точці області D, отримаємо поле напрямків.
в кожній точці області D, отримаємо поле напрямків.