 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задачі на складання д. р
10. Задача про радіоактивний розпад. Відомо, що швидкість розпаду радію в момент часу t пропорційна наявній в цей момент масі m(t). Знайти закон радіоактивного розпаду, якщо відомо, що початкова маса дорівнювала Розв’язання. Позначимо
- середня швидкість розпаду, яка показує на скільки одиниць змінюється маса за одиницю часу. Границя цього відношення при
Згідно фізичного закону маємо
де k - коефіцієнт пропорційності. Д. р. (1) є рівнянням радіоактивного розпаду, воно відноситься до д. р. з відокремлюваними змінними. Розв’яжемо його
Зауважимо, що в останньому випадку довільну сталу при інтегруванні ми взяли у формі ln C, це для того, щоб легше було звільнитися від логарифмів. Крім того, відомо, що lne=1, тому Отже, далі запишемо
Функція (2) є загальним розв’язком д. р. (1). Згідно з початковою умовою
Таким чином, запишемо
Знайдемо тепер коефіцієнт пропорційності за умовою, що за t=23 роки маса зменшується на 1%, тобто від початкової маси
Відомо, що для еквівалентних нескінченно малих Далі маємо
Отже закон радіоактивного розпаду радію
Знайдемо період напіврозпаду Т. Це час Т, за який початкова маса
Внаслідок логарифмування знаходимо
20.Задача про випуск продукції при сталій ціні. Нехай до моменту часу t реалізовано продукції певної галузі в обсязі Позначимо через
де l - коефіцієнт пропорційності. Вважаючи, що величина інвестиції складає фіксовану величину доходу
де m так звана норма інвестиції (m-const),
- диференціальне рівняння закону випуску продукції, де Розв’яжемо д. р. (3):
. Позначимо
- загальний розв’язок. За початковою умовою
Якщо при
Отже, ми знайшли закон випуску продукції в залежності від часу. Зауважимо, що д. р. (3) описує також ріст народонаселення, динаміку росту цін при постійній інфляції, процес радіоактивного розпаду (див. попередню задачу) та ін. 30. Задача про випуск продукції при змінній ціні. Із збільшенням об’єму виробництва продукції
яке далі залишається рівнянням з відокремлюваними змінними. Розглянемо наступний приклад. Приклад. Знайти закон зміни обсягу реалізованої продукції
відомий коефіцієнт пропорційності між швидкістю випуску продукції та інвестицією Розв’язання. Рівняння (5) в умовах задачі матиме вигляд
Дріб розкладемо на прості:
Тоді
При
- закон обсягу випуску продукції при змінній ціні. Зауважимо, що подібними рівняннями описується процес поширення інформації (реклами), динаміка епідемій, процес розмноження бактерій в обмеженому середовищі та ін. 40. Ефективність реклами. Припустимо, що в торгівельній мережі реалізується продукція В, про яку в момент часу t з числа потенціальних покупців N знають лише x. Для прискорення збуту продукції В, по радіо та телебаченню були дані рекламні оголошення. Вважаємо, що після рекламних оголошень швидкість зміни числа покупців, які знають про продукцію В, пропорційна як числу тих, хто знає про товар, так і числу покупців, які про нього не знають. Домовимось, що час відраховується після рекламних оголошень, коли про товар знало Розв’язання. За час
Останнє рівняння відрізняється від д. р. (6) тільки позначеннями, тому аналогічно попередньому отримуємо:
Відповідно до початкової умови (
Із співвідношення
знаходимо
Крива, побудована відповідно до рівняння (9) має вигляд зображений на рисунку і носить назву логістичної кривої.
Рис.
Поиск по сайту: |
 . Знайти також період напіврозпаду радію, якщо встановлено, що за 23 роки маса зменшується на 1%.
. Знайти також період напіврозпаду радію, якщо встановлено, що за 23 роки маса зменшується на 1%. величину маси в момент часу t. Нехай за проміжок часу від t до
величину маси в момент часу t. Нехай за проміжок часу від t до  внаслідок розпаду маса зменшилась на
внаслідок розпаду маса зменшилась на  , тоді
, тоді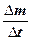 -
- дорівнює миттєвій швидкості розпаду в момент часу t, тобто
дорівнює миттєвій швидкості розпаду в момент часу t, тобто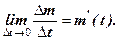
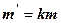 , (1)
, (1)
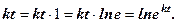
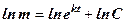 , або
, або 
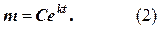
 із (2) при
із (2) при  отримуємо
отримуємо
 .
.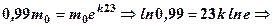
 .
. , тому
, тому 


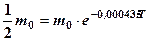 .
.
 . Отже,
. Отже, (років).
(років). . Припустимо, що вся вироблена продукція реалізується за сталою ціною p, тобто, ринок ненасичений. Тоді величина доходу буде дорівнювати
. Припустимо, що вся вироблена продукція реалізується за сталою ціною p, тобто, ринок ненасичений. Тоді величина доходу буде дорівнювати 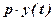 .
. величину інвестиції, що направляється на розширення виробництва, при цьому знехтуємо часом між закінченням виробництва продукції і її реалізацією. Припустимо далі, що швидкість випуску продукції пропорційна величині інвестиції, тобто
величину інвестиції, що направляється на розширення виробництва, при цьому знехтуємо часом між закінченням виробництва продукції і її реалізацією. Припустимо далі, що швидкість випуску продукції пропорційна величині інвестиції, тобто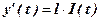 , (1)
, (1) , (2)
, (2) . Із (1) і (2) отримаємо
. Із (1) і (2) отримаємо - (3)
- (3) ,
,
 , тоді
, тоді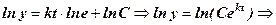
 -
-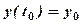 знаходимо С:
знаходимо С: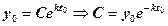 , тоді
, тоді . (4)
. (4) обсяг продукції дорівнював
обсяг продукції дорівнював  , тобто
, тобто .
. на реалізовану продукцію (крива попиту) є спадною функцією, тому д. р. (3) тепер прийме вигляд
на реалізовану продукцію (крива попиту) є спадною функцією, тому д. р. (3) тепер прийме вигляд , (5)
, (5) , якщо відомо, що крива попиту задана рівнянням
, якщо відомо, що крива попиту задана рівнянням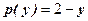 ,
, (див. (1)) , норма інвестиції
(див. (1)) , норма інвестиції  ,
,  (умовних одиниць).
(умовних одиниць). (6)
(6)



 .
.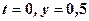 знаходимо С:
знаходимо С: 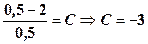 . Отже,
. Отже, 

 - (7)
- (7) людей. Знайти залежність числа x – проінформованих покупців від часу t.
людей. Знайти залежність числа x – проінформованих покупців від часу t. кількість проінформованих покупців зміниться на
кількість проінформованих покупців зміниться на 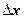 .
.  - середня швидкість зміни проінформованих покупців,
- середня швидкість зміни проінформованих покупців, 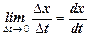 - швидкість зміни x в момент часу t. За умовою задачі маємо
- швидкість зміни x в момент часу t. За умовою задачі маємо ,
,  . (8)
. (8)


 .
. ) маємо
) маємо


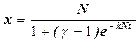 . (9)
. (9)