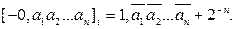Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную системы счисления и наоборот

Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную системы счисления

Двоичная система счисления имеет основание 2 и две цифры: 0 и 1.

Восьмеричная система имеет основание 8 и цифры: 0, 1, …, 7.

Шестнадцатеричная система имеет основание 16 и цифры: 0, 1, …, 9, A, B, C, D, E, F.

Ниже приведена таблица 1 соответствия чисел от 0 до 15 в данных системах счисления.

Таблица 1 Соответствие чисел в разных системах счисления

Для преобразования целого числа Z_p→Z_q в случае q=p^r, где r – целое число, большее единицы, достаточно Z_p разбить справа налево на группы по r цифр и каждую из них независимо перевести в систему q.

Т.е. для перевода любого целого двоичного числа в восьмеричное (8=2³) необходимо разбить его справа налево на группы по 3 цифры (триады, самая левая группа может содержать менее трех двоичных цифр), а затем каждой группе поставить в соответствие ее восьмеричный эквивалент.

Пример 10. Перевести число 11011001 из двоичной системы в восьмеричную.

11011001₍₂₎=11011001=331₍₈₎

т.к. 11₍₂₎=3₍₈₎,

011₍₂₎=3_(8),

001₍₂₎=1₍₈₎.

А перевод целого двоичного числа в шестнадцатеричное (16=2⁴) производится путем разбиения данного числа на группы по 4 цифры (тетрады).

Пример 11. Перевести число 1100011011001 из двоичной системы в шестнадцатеричную.

1100011011001 ₍₂₎=1100011011001=18D9₍₁₆₎

т.к. 1₍₂₎=1₍₁₆₎,

1000₍₂₎=8₍₁₆₎,

1101₍₂₎=D_(16),

1001₍₂₎=9₍₈₎.

Задания.

Перевести следующие числа из двоичной системы счисления в восьмеричную и шестнадцатеричную:

1) 1110101011₍₂₎à?_{(8), (16)}

2) 10101001011₍₂₎à? _{(8), (16)}

3) 11110101101₍₂₎à? _{(8), (16)}

4) 1000010111110₍₂₎à? _{(8), (16)}

5) 101010101₍₂₎à? _{(8), (16)}

6) 1011010101101₍₂₎à? _{(8), (16)}

1.3.2 Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную

Для преобразования целого числа Z_p→Z_q в случае p=q^r, где r – целое число, большее единицы, достаточно каждую цифру числа Z_p заменить соответствующим r-разрядным числом в системе счисления q, дополняя его при этом нулями слева до группы в r цифр.

То есть, перевод восьмеричных и шестнадцатеричных чисел в двоичные производится обратным путем – сопоставлением каждому знаку числа соответствующей триады (тетрады).

Пример 12. Перевести число 331 из восьмеричной системы в двоичную.

331₍₈₎=11011001=11011001.

т.к. 3₍₈₎=11₍₂₎, (первое число не обязательно дополнять до триады)

3₍₈₎=11₍₂₎, а если дополнит до триады, то 011,

1₍₈₎=1₍₂₎, а если дополнить до триады, то 001.

Пример 13. Перевести число 18D9 из шестнадцатеричной системы в двоичную.

18D9 ₍₁₆₎=1100011011001=1100011011001 ₍₁₆₎

т.к. 1₍₁₆₎=1₍₂₎,

8₍₁₆₎=1000₍₂₎,

D₍₁₆₎=1101_(2),

9₍₈₎=1001₍₂₎.

Задания.

Перевести следующие числа из восьмеричной и шестнадцатеричной системы счисления в двоичную:

1) 3A74₍₁₆₎à?₍₂₎ 7) 2A9C₍₁₆₎à?₍₂₎

2) 746₍₈₎à?₍₂₎ 8) 2535₍₈₎à?₍₂₎

3) 7BCD₍₁₆₎à?₍₂₎ 9) 152E₍₁₆₎à?₍₂₎

4) 253₍₈₎à?₍₂₎ 10) 1624₍₈₎à?₍₂₎

5) 1F67₍₁₆₎à?₍₂₎ 11) 7FD₍₁₆₎à?₍₂₎

6) 637₍₈₎à?₍₂₎ 12) 251₍₈₎à?₍₂₎

Кодирование чисел. Прямой, обратный и дополнительный коды. Сложение чисел с фиксированной запятой в прямом, обратном и дополнительных кодах

В современных ЭВМ используется 2 способа представления двоичных чисел – с фиксированной и с плавающей запятой. В формате с фиксированной запятой используется как беззнаковое представление чисел, так и представление чисел со знаком, где знак кодируется двоичной цифрой – обычно плюсу соответствует 0, а минусу – 1. Под код знака обычно отводится старший разряд a₀ двоичного вектора a₀a₁a_2…a_n, называемый знаковым.

Запятая может быть фиксирована после любого разряда двоичного числа, но чаще всего используется 2 формата: целые числа, когда запятая фиксируется после младшего разряда a_n, и дробные числа – запятая фиксируется после a₀.

Мы будем рассматривать дробные числа a₀,a₁a_2…a_n.

Кодирование чисел

Прямой код

Пусть А= a₀,a₁a_2…a_n.Если A>0, то А= 0,a₁a_2…a_n, если же A<0, то А= =1,a₁a_2…a_n.Приведенное кодирование дробных двоичных чисел со знаком принято называть прямым кодом числа и обозначается [A]_d. То есть,

Пример 14.Если A=0,110101, то [A]_d=0,110101.

Если A=-0,101110, то [A]_d=1,101110.

Обратный код

Представление обратного кода определяется следующим соотношением:

Т.е. обратный код положительного числа равен самому числу. Для получения обратного кода отрицательного числа достаточно присвоить знаковому разряду значение 1 и проинвертировать все остальные разряды числа.

Для перехода из обратного кода в прямой осуществляется преобразование т.е. [[A]_i]=[A]_d.

Пример 15.Если A=-0,111000, то [A]_i=1,000111.

Если A=-0,101110, то [A]_i=1,010001.

Дополнительный код

Представление дополнительного кода определяется следующим соотношением:

Дополнительный код положительного числа равен самому числу. Дополнительный код отрицательного числа дополняет исходное число до основания системы счисления. Дополнительный код отрицательного числа образуется в соответствии:

Первый способ.Для преобразования отрицательного числа в дополнительный код следует преобразовать его сначала в обратный код и добавить единицу к младшему разряду обратного кода.

Второй способ: оставить без изменения все младшие нули и одну младшую единицу, остальные разряды проинвертировать.

Пример 16.Если A=-0,111000, то [A]_i=1,000111, а [A]_c=1,001000.

ЕслиA=-0,101110, то[A]_i=1,010001, а[A]_c=1,010010.

Задания.

Перевести следующие числа в прямой, обратный и дополнительный код:

1) 0,0111 6) -0,11110101

2) -0,0111 7) 0,1010110

3) -0,1000 8) -0,1000110

4) -0,0101 9) 0,10100000

5) -0,10100010 10) -0,10111000

Поиск по сайту: