 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вычисление вероятностей ⇐ ПредыдущаяСтр 5 из 5
Рассмотрим биномиальное распределение, для которого известны величины n и π. Необходимо найти вероятность того, что X будет в точности равно некоторому значению а. Существует формула для вычисления вероятности, которая оказывается полезной в случае малых и средних значений n. (При больших n можно использовать более простое, по сравнению с представленным здесь строгим, решение, основанное на нормальном распределении. Его мы рассмотрим в разделе 7.4.) Кроме того, в статистических таблицах (например, в табл. В.3 приложения В книги Э. Сигел ……… приводятся точные значения вероятностей биномиального распределения и кумулятивные вероятности для п от 1 до 20 и π = 0,05, 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,7, 0,8, 0,9 и 0,95. Точная формула имеет следующий вид.
Р(х=а) =
Если применить эту формулу для каждого из значений а от 0 до п (иногда этот процесс оказывается очень трудоемким), можно полностью вычислить распределение вероятности. Затем, складывая необходимые из полученных таким образом значений, можно вычислить вероятность для любого интересующего нас значения X. Рассмотрим пример применения приведенной выше формулы. Предположим, что существуют n = 5 возможных попыток, причем вероятность успеха каждой из них равна π = 0,8. Найдем вероятность в точности а = 3 успешных попыток. Ответ вычисляем следующим образом:
Р(х=3) = (Обозначение n! читается как «n факториал» и означает произведение целых чисел от 1 до n. Принято также считать, что 0! = 1.) Это вероятность в точности трех успешных попыток. Если необходимо найти также вероятность достижения успеха три или более раз, необходимо провести расчеты по этой формуле еще два раза: один раз при а = 4 и один раз при а =5. Вероятность достижения успеха три или более раз будет равна сумме полученных значений. Для вычисления вероятностей можно также воспользоваться компьютером, как показано ниже. Функция = БИНОМРАСП(а, n, π, ЛОЖЬ) для Р(х=а), и БИНОМРАСП(а, n, π, ИСТИНА) для Р(х<=a). Функция плотности вероятности и функция кумулятивного распределения Биномиальное распределение с n =5 и р = 0,800000
а Р(х=а) Р(х<=a) 0 0,00032 0,00032 1 0,0064 0,00672 2 0,0512 0,05792 3 0,2048 0,26272 4 0,4096 0,67232 5 0,32768 1
После вычисления отдельных значений вероятности (для 3, 4 и 5 успешных попыток) получаем искомый результат: Р(Х Таким образом, вероятность достижения успеха три или более раз из пяти возможностей составляет 94,2%. Кроме того, в соответствии с правилом дополнительности, вероятность три или более должна быть равна единице минус вероятность два или менее, которая представлена среди результатов компьютерных вычислений числом 0,0579. Используя это значение, находим ответ: 1 - 0,0579 = 0,9421.
При вычислении вероятностей биномиального распределения с помощью Excel, чтобы получить вероятность Р(Х=а) того, что результат окажется равным а, необходимо использовать формулу = БИНОМРАСП (а, n, π, ЛОЖЬ), а для вычисления вероятности Р(Х
Пример. Сколько крупных клиентов позвонят завтра?
Сколько крупных клиентов вашей фирмы (всего у вас есть 6 крупных клиентов) позвонят завтра? Вы склонны предполагать, что каждый из них может позвонить с вероятностью π = 0,25 и что обращаются к вам они независимо друг от друга. Если так, то количество крупных клиентов, которые позвонят завтра, имеет биномиальное распределение. Сколько звонков от крупных клиентов можно ожидать? Другими словами, чему равно ожидаемое значение X? Вот ответ на этот вопрос: Е(Х) = n Чему равна вероятность того, что позвонят именно двое из шести крупных клиентов? Ответ на этот вопрос имеет следующий вид:
Р(Х = 2) = Ниже приведено полное распределение вероятности для количества звонков от крупных клиентов, которые поступят завтра, включая все возможные случаи от 0 до n =6. Функция плотности вероятности и функция кумулятивного распределения Биномиальное распределение n=6 и р=0,25.
а Р(х=а) Р(х<=a) 0 0,177978516 0,177978516 1 0,355957031 0,533935547 2 0,296630859 0,830566406 3 0,131835938 0,962402344 4 0,032958984 0,995361328 5 0,004394531 0,999755859 6 0,000244141 1
Обратите внимание, что наиболее вероятными оказываются один или два звонка, как и следовало ожидать при среднем значении 1,5 звонка. Воспользовавшись этим распределением вероятности, можно вычислить любую представляющую интерес вероятность, характеризующую обращение крупных клиентов в фирму завтра по телефону. Вероятность того, что позвонят все шесть клиентов, невелика (0,0002, или 0,02%, это значительно меньше вероятности в 1%). Вероятность того, что позвонят 4 или более из них, составляет 0,0330 + 0,0044 + 0,0002 = 0,0376. Вероятность того, что день будет совершенно спокойный, без звонков от крупных клиентов, составляет 0,178. Полное распределение вероятности для данного случая показано на рис. 7.2.2.
Пример. Сколько логических анализаторов запланировать для производства?
Качеству выпускаемого товара уделяется большое внимание, однако логические анализаторы настолько сложны, что их производство все еще не лишено определенных недостатков. Из предыдущего опыта известно, что около 97% готовой продукции работает хорошо. Сегодня предстоит отгрузить потребителю 17 таких устройств. Вопрос состоит в следующем: сколько устройств надо выпустить, чтобы иметь разумные гарантии того, что можно будет отгрузить 17 работающих должным образом логических анализаторов? Разумно предположить, что количество работающих устройств подчиняется биномиальному распределению, где n — количество запланированных для производства устройств, а π - вероятность того, что каждое из них работает должным образом (эта вероятность равна 0,97). Такое предположение даст возможность рассчитать вероятность надлежащего функционирования 17 или более устройств, выпущенных в соответствии с производственным планом. Что произойдет, если в плане предусмотреть выпуск 17 устройств, не предусмотрев возможности дефектов? В этом случае может показаться, что высокий уровень выхода годного товара (97%) сыграет свою положительную роль, но в действительности вероятность того, что все 17 устройств будут работать хорошо (при n =17 и a =17), составит только 0,596:
a P(X=a) 10 3,13647E-07 11 6,45352E-06 12 0,000104332 13 0,001297462 14 0,011986074 15 0,077509946 16 0,313269363 17 0,595826044
Рис. 7.2.3. Распределение вероятности для данного случая Таким образом, если в производственный план внести то же количество товара, что и необходимо отгрузить, 17 единиц, риск окажется очень большим! Вероятность того, что удастся выполнить заказ, окажется равной только 59,6%, а с вероятностью 40,4% отправить товар соответственно заказу и в рабочем состоянии не удастся. Распределение вероятности для данного случая показано на рис. 7.2.3. Похоже, что лучше включить в план выпуск не 17, а большего количества устройств. Что если в производственный план внести выпуск n = 18 устройств? Для того чтобы найти вероятность того, что удастся отгрузить по меньшей мере 17 работающих должным образом устройств, необходимо сложить вероятности для a = 17 и a = 18:
а Р(Х=а) 10 2,11712E-08 11 4,97843E-07 12 9,38988E-06 13 0,000140126 14 0,00161812 15 0,01395179 16 0,084582728 17 0,321746064 18 0,577951263
Р(Х ≥ 17) = Р(Х=17) + Р(Х=18) = 0,322 + 0,578 = 0,900.
Таким образом, если в производственный план заложить выпуск 18 устройств, вероятность успешной отгрузки 17 работающих устройств составит 90%. Этот результат выглядит неплохо, однако все еще необходимо учитывать то, что возможность неудачи составляет 10%. Соответствующее распределение вероятности показано на рис. 7.2.4.
Рис. 7.2.4.
Аналогичные расчеты показывают, что если внести в производственный план выпуск 19 устройств, то вероятность получить для отгрузки потребителю 17 работающих устройств составит 98,2% (9,2% + 32,9% + 56,1%). Таким образом, для того, чтобы в достаточной мере гарантировать успешное выполнение заказа на 17 работающих устройств, в план следует внести выпуск по меньшей мере 19 устройств.
а Р(Х=а) 17 0,091697628 18 0,32943222 19 0,560612725
Поиск по сайту: |

 = 0,2048
= 0,2048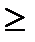 3) = Р(Х=3) + Р(Х=4) + Р(Х=5) = 0,2048 + 0,4096 + 0,3277 = 0,9421.
3) = Р(Х=3) + Р(Х=4) + Р(Х=5) = 0,2048 + 0,4096 + 0,3277 = 0,9421. а) того, что результат окажется меньше чем, или равным а, использовать формулу = БИНОМРАСП (а, n, π, ИСТИНА).
а) того, что результат окажется меньше чем, или равным а, использовать формулу = БИНОМРАСП (а, n, π, ИСТИНА). π = 1,5 звонков от крупных клиентов. Стандартное отклонение составляет σx =
π = 1,5 звонков от крупных клиентов. Стандартное отклонение составляет σx =  = 1,060660. Это означает, что следует ожидать на один или два звонка больше или меньше значения 1,5, полученного в результате вычислений. Несмотря на то, что это значение дает некоторое представление о количестве звонков, которое можно ожидать, полученный результат еще не характеризует вероятность того, что такое количество клиентов действительно позвонят. Вычислим теперь соответствующие вероятности.
= 1,060660. Это означает, что следует ожидать на один или два звонка больше или меньше значения 1,5, полученного в результате вычислений. Несмотря на то, что это значение дает некоторое представление о количестве звонков, которое можно ожидать, полученный результат еще не характеризует вероятность того, что такое количество клиентов действительно позвонят. Вычислим теперь соответствующие вероятности. = 15×0,0625×0,316406 = 0,297.
= 15×0,0625×0,316406 = 0,297.

