 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение биномиального распределения и биномиального соотношения
Рассмотрим некоторое конкретное событие. Каждый раз при выполнении случайного эксперимента это событие или происходит, или нет. Наличие двух возможных результатов и определяет приставку би- (т.е. “двух-”) в слове биномиальное. Случайная величина X, которая представляет собой число наступлений определенного события в результате п попыток, имеет биномиальное распределение в следующих случаях. 1. Если в каждой из п попыток вероятность наступления события π одна и та же. 2. Если все попытки независимы друг от друга. Требование независимости означает невозможность “заглядывать”, как, например, в случае распределения заказов особого блюда посетителями ресторана. Если некоторые из посетителей делают заказ этого блюда потому, что видят, как другие явно им наслаждаются (мысленно восклицая “Я тоже хочу это!”), количество заказов не будет соответствовать биномиальному распределению. Для того чтобы распределение заказов оказалось биномиальным, все посетители должны делать свой выбор независимо. Биномиальная пропорция р — это представление имеющей биномиальное распределение случайной переменной X в виде доли общего количества попыток n.
p =
(Обратите внимание на то, что π — это фиксированное число, определяющее вероятность наступления события, а р — случайная величина, зависящая от наблюдаемых данных.) Например, если в результате опроса n = 600 покупателей было установлено, что X = 38 из них собираются покупать ваш товар, биномиальная пропорция оказывается равной
p = Выражающее биномиальную пропорцию (соотношение) число р называют также биномиальной долей. Его можно воспринимать еще и как относительную частоту, с которой мы уже встречались в главе 6.
Пример. Сколько подано заявок? Сложный путь вычислений
В этом примере показан сложный способ исследования биномиальной случайной величины. Несмотря на то, что необходимость в построении дерева вероятностей возникает достаточно редко, поскольку оно обычно довольно велико, на него полезно один раз посмотреть, чтобы понять, что же в действительности происходит в случае биномиального распределения. Более того, когда будет представлен более короткий (более легкий) способ вычислений, вы поймёте с благодарностью, как много времени вы экономите! Предположим, что нас интересуют следующие n = 3 звонка в отдел торговли по каталогам, а из опыта известно (или мы так предполагаем), что π = 0,6, т.е. 60% обращений приводят к получению заказа на покупку (другие звонки связаны с запросом информации или неправильным соединением). При решении задач с биномиальным распределением вероятность π обычно дается в условии. В реальной жизни у этой вероятности те же источники, о которых мы вели речь ранее: относительная частота, теоретические расчеты и субъективные оценки. Что можно сказать о количестве обращений, которые приведут в данном случае к оформлению заказа? Понятно, что это число окажется равным 0,1,2 или 3. Поскольку каждый звонок скорее приведет к подаче заявки, чем нет, следует, видимо, ожидать, что вероятность подачи трех заявок будет больше, чем вероятность того, что не будет подано ни одной заявки. Но как найти эти вероятности? Дерево вероятностей на рис. 7.2.1. а дает полное описание ситуации и иллюстрирует результат каждого из трех телефонных звонков.
Обратите внимание на то, что показанные вдоль ветвей условные вероятности всегда равны 0,60 и 0,40 (это вероятности для каждого из телефонных звонков), поскольку мы считаем, что заказы делаются независимо и звонящие в отдел лица не влияют друг на друга. Количество заказов показано на рис. 7.2.1а) в крайнем правом столбце; например, второе сверху число, 2, отражает тот факт, что в первом и во втором телефонном звонках (но не в третьем) были сделаны заказы и, таким образом, были получены два заказа. Обратите внимание на то, что существуют три способа (и, соответственно, три пути на дереве) получить два заказа. Для того чтобы построить распределение вероятности количества полученных заказов, можно сложить все вероятности различных способов реализации данного количества заказов.
Полученное распределение вероятности показано на рис. 7.2.1б). Из распределения вероятности можно найти любую необходимую вероятность простым сложением соответствующих значений. Так, например, вероятность получения по меньшей мере двух заказов равна 0,432 + 0,216 = 0,648. Используя формулы для вычисления среднего значения и стандартного отклонения, приведенные в разделе 7.1, можно найти среднее (1,80 заказа) и стандартное отклонение (0,849 заказа). Однако все это требует слишком больших затрат труда. Существует формула, которая позволяет значительно быстрее найти среднее, стандартное отклонение и необходимые вероятности. Несмотря на то, что в данном простом примере все эти значения можно вычислить непосредственно, ситуация не всегда складывается так удачно. Так, например, если бы мы рассматривали не 3, а 10 последовательных звонков, в правой части дерева было бы не 8 вероятностей, как на рис. 7.2.1а, а 1024 вероятностей. В приведенном примере мы рассмотрели предложенную ситуацию, выделили все возможные комбинации и затем перешли к распределению вероятности: количества наступлений события. Концептуально это правильный путь рассмотрения ситуации. А теперь мы рассмотрим легкий путь вычислений необходимых значений.
Поиск по сайту: |
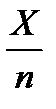 =
= 