 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вычисление среднего и стандартного отклонения
Среднее, или ожидаемое значение, дискретной случайной величины представляет собой некоторое определенное число, характеризующее типичное значение этой величины, подобно тому, как некоторый набор данных характеризуется средним значением. Среднее для случайной величины Х обозначают либо малой греческой буквой µ (мю), либо Е(Х) (читается “ожидаемое значение X"). Формула для вычисления среднего имеет следующий вид.
µ = Е(Х) =
Если бы вероятности всех значений были одинаковыми, мы получили бы простое усреднение всех значений. Вообще говоря, среднее значение случайной величины можно определить как взвешенное среднее всех возможных значений, в котором в качестве весов выступают соответствующие вероятности. В рассмотренном выше примере средний доход вычисляется следующим образом: Ожидаемый доход = (10 * 0,20) + (5 * 0,40) + (1 * 0,25) + (-4 * 0,15) = 3,65. Таким образом, ожидаемый доход составляет 3,65 миллионов долларов. Это значение характеризует все различные возможные результаты (10, 5, 1, -4) одним числом, которое учитывает вероятность (правдоподобие) каждого из них. Стандартное отклонение дискретной случайной величины приблизительно указывает, насколько реальные значения этой случайной величины могут отличаться от среднего. Во многих случаях в коммерческой деятельности стандартное отклонение характеризует риск, показывая, насколько неопределенной является ситуация. Стандартное отклонение обозначается
В приведенном выше примере стандартное отклонение, дохода вычисляется следующим образом:
σ =
Стандартное отклонение в размере $4 400 000 показывает, что в данном случае присутствует значительный риск. Доход вполне может оказаться на $4 400 000 выше или ниже среднего значения в $3 650 000. На рис.7.1.1. показано распределение вероятностей. Высота вертикальной линии соответствует вероятности, а положение линии – величине дохода для каждого случая. Показано также ожидаемое значение, 3 650 000, и стандартное отклонение, 4 400 000.
Рис. 7.1.1. Распределение вероятности будущих доходов. Показано также среднее значение (ожидаемый доход) и стандартное отклонение (риск)
Пример. Оценка риска и доходности
Перед вами стоит задача — оценить три разных проекта (X,Y иZ) и разработать рекомендации для высшего руководства. По каждому из проектов необходимы инвестиции в объеме $12 000, а возврат средств планируется на следующий год. По проекту X гарантированный возврат составит $14 000. По проекту Y может быть получено либо $ 10 000, либо $20 000, вероятность в каждом случае составляет 0,5. Проект Z не даст ничего с вероятностью 0,98 или принесет $1 000 000 с вероятностью 0,02. Эти данные собраны в табл.7.1.2. Табл. 7.1.2.
Средние значения найти достаточно просто: для проекта X это $14 000, для Y среднее значение находится как 10000 * 0,50 + 20 000 * 0,50 = $15 000, а для проекта Z среднее составляет: 0 * 0,98 + 1 000000 * 0,02 = $20 000. Мы можем записать это следующим образом: Е(Х) = µх= $14 000, E(Y) = µy = $ 15 000, E(Z) = µz = $20 000 Если исходить только из этих величин, проект Z может показаться самым лучшим, а проект X — худшим из всех. Однако средние значения не дают полной информации. Так, например, несмотря на то, что по проекту Z ожидаемый возврат оказывается самым большим, этот проект несет еще и максимальный риск: вероятность отсутствия каких-либо выплат составляет 98%! Присущие каждому из рассматриваемых случаев риски характеризуются стандартным отклонением. σх = σy = σz =
Исследование стандартного отклонения подтверждает возникшие опасения. Проект Z действительно оказывается самым рискованным — намного более рискованным, чем два других. Проект X — самый безопасный. Это верное дело, не несущее никакого риска. В случае проекта Y риск составляет $5 000. Какой проект выбрать? На этот вопрос нельзя ответить, используя только методы статистического исследования. Несмотря на то, что ожидаемое значение и стандартное отклонение предоставляют нам полезные для принятия решения данные, задача этим не исчерпывается. Обычно предпочтение отдается большим ожидаемым выплатам и меньшему риску. Однако в приведенном примере возможность получения больших выплат сопряжена с более высоким риском. Окончательный выбор проекта требует от вас (и от вашей фирмы) определить, что важнее — доход или риск, — и, исходя из этого, определить, оправдывает увеличение ожидаемых выплат такое увеличение риска или нет. Что если попробовать оценить проекты в терминах дохода, а не выплат? Поскольку каждый проект требует инвестиций в $ 12000, для перехода от выплат к доходу необходимо вычесть $ 12000 из каждой величины выплат в таблице распределения вероятностей. Доход = Выплаты - $ 12 000. Применяя правила из раздела 5.2, которые так же справедливы для характеристик случайных величин, как и для характеристик наборов данных, вычтем $ 12 000 из каждого среднего значений и оставим без изменений стандартные отклонения. Таким образом, без дополнительных подробных вычислений мы получаем следующие величины ожидаемого дохода: X: $2 000 (14 – 12 = 2). Y:$3 000 Z: $8 000 Стандартные отклонения для дохода такие же, как и для размера выплат: X: $0, Y; $5 000, Z: $140 000
Поиск по сайту: |

 , что соответствует использованию нами буквы
, что соответствует использованию нами буквы 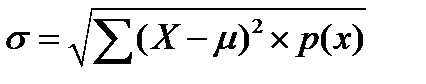

 = 4,40.
= 4,40. = $ 0
= $ 0 = $ 5 000
= $ 5 000 = $ 140 000
= $ 140 000