 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Оценка показателей эффективности инвестиционного проекта
Чистый дисконтированный доход (ЧДД, интегральный эффект, чистая текущая стоимость, NPV) – накопленный дисконтированный чистый доход (сальдо реальных денег, эффект) за весь расчетный период, определяемый по формуле:
где ЧДt – чистый доход на tом шаге расчета; Кt – капиталообразующие инвестиции на tом шаге расчета; Е – норма дисконта; Т – горизонт расчета проекта. Для принятых в расчете одинаковых значений ЧДt на каждом временномшаге ЧДД проекта можно определить с учетом формулы текущей стоимости периодических аннуитетных результатов:
Т = Тс + Тэ, (17) где Тс – срок строительства в годах; Тэ – плановый период эффективной реализации проекта (эксплуатации объектов) с получением эффектов. В рассматриваемом примере: - Тс =2 года, Тэ = 20 лет, Т = 2 + 20 = 22 лет; - принятое значение Е = 0,12; - размер годового чистого дохода ЧДгод = 80150,3 тыс.руб.; - капиталообразующие инвестиции всего: К = 135637,8 тыс.руб. в том числе К1 –68497,1 тыс. руб. К2 – 67140,7 тыс.руб.
Находим сумму дисконтированных капиталообразующих затрат:
= 114682,3 тыс.руб. Дисконтированные доходы:
Отсюда ЧДД = 477262,5 – 114682,3 = 362580,2 тыс.руб. ЧДД > 0 – проект (инвестиции) эффективен. Индекс доходности проекта определяется отношением накопленных дисконтированных притока и оттока реальных денег
Внутренняя норма доходности (ВНД) Внутренняя норма доходности проекта определяет значение нормы дисконта, выше которого проект перестает быть эффективным. Этот показатель характеризует реальную предельную доходность капиталообразующих инвестиций в проект в течение продолжительности периода его экономической оценки. Для проекта, требующего на нулевом шаге инвестиции в размере К и в дальнейшем обеспечивающего постоянный доход (Д) в течение неограниченного срока ВНД (Евн) = Для других проектов с неравномерными денежными потоками в расчетном периоде ВНД проекта находится из условия:
При значении нормы дисконта равном «Евн» чистый дисконтированный доход проекта обращается в нулевую сумму:
С учетом этого нахождение ВНД удобно осуществлять графическим способом, строя функцию ЧДД = ¦(Е), и находя значение Евн для нулевой величины ЧДД. Поскольку график данной зависимости носит нелинейный характер, то его построение должно осуществляться минимум по пяти-семи точкам (для пяти-семи значений Е). В рассматриваемом примере для Е = 0,12 полученное значение ЧДД составило 362580,2 тыс.руб. Примем Е=0,2 Получим:
Так как ЧДД > 0, следует двигаться в сторону увеличения Е. Примем Е = 0,30.
= 64837,3 тыс.руб. Так как ЧДД > 0, примем следующее значение Е=0,4.
руб. Так как ЧДД > 0, примем следующее значение Е=0,45
= 5490,9 тыс. руб Так как ЧДД>0, примем следующее значение Е=0,5
= - 4281,9 тыс. руб Полученное значение ЧДД <0, следовательно, 0,45<Евн< 0,5. Окончательное значение Евн найдем на графике ЧДД = ¦(Е), координаты которого будут иметь значения:
График функции ЧДД = ¦(Е) покажем на рис. 1.
  
 
Рис.1. График зависимости ЧДД проекта от принятого значения Е
Таким образом Евн = 0,475, что соответствует доходности инвестиций 47,5 % годовых. Полученное значение Евн = 0,475 (47,5 %), больше рекомендуемой эталонной нормы прибыли для данной группы инвестиционных проектов Е = 0,12 (12 %), следовательно проект экономически эффективен.
Поиск по сайту: |
 , (15)
, (15) , (16)
, (16)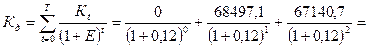 0 + 61158,1 + 53524,2 =
0 + 61158,1 + 53524,2 = 477262,5 тыс.руб.
477262,5 тыс.руб. . (18)
. (18) 4,16 > 1 – проект эффективен.
4,16 > 1 – проект эффективен. . (19)
. (19) . (20)
. (20) . (21)
. (21) тыс. руб.
тыс. руб. 157255,6 – 92418,3 =
157255,6 – 92418,3 = 102110,3 – 83182,1 = 18928,2 тыс.
102110,3 – 83182,1 = 18928,2 тыс. 84664,1 – 79173,2 =
84664,1 – 79173,2 = 71233,3 – 75505,2 =
71233,3 – 75505,2 =