Размерные цепи. Способ равных допусков и способ допусков одного квалитета при решении размерных цепей

При конструировании механизмов, машин, приборов и других изделий, проектировании технологических процессов, выборе средств и методов измерений возникает необходимость в проведении размерного анализа, с помощью которого достигается правильное соотношение взаимосвязанных размеров и определяются допустимые ошибки (допуски). Подобные геометрические расчеты выполняются с использованием размерных цепей.

Размерной цепьюназывается совокупность взаимосвязанных размеров,непосредственно участвующих в решении поставленной задачи, образующих замкнутый контур и определяющих взаимное положение поверхностей (или осей) одной или нескольких деталей.

Сущность расчета размерной цепи заключается в установлении допусков и предельных отклонений всех ее звеньев исходя из требований конструкции и технологии. При этом различают две задачи: прямая и обратная.

Прямая задача заключается в определении номинальных размеров, допусков и предельных отклонений всех составляющих звеньев размерной цепи по заданным номинальному размеру и допуску (отклонениям) исходногозвена. Такая задача относится к проектному расчету размерной цепи.

Обратная задача заключается в определении номинального размера, допуска и предельных отклонений замыкающего звена по установленным номинальным размерам, допускам и предельным отклонениям составляющихзвеньев. Такая задача относится к поверочному расчету размерной цепи.

Прямую задачу можно решать одним из способов:

Способ равных допусков применяют, когда все размеры цепи входят в один интервал диаметров и могут быть выполнены с примерно одинаковой точностью, т. е. можно принять

T1 =T2 =…=Tср, зная что допуск размера замыкающего звена равен сумме допусков размеров составляющих звеньев, получаем , где k – количество звеньев размерной цепи, включая замыкающее звено.

Этот допуск корректируют для некоторых составляющих размеров в зависимости от их значений, конструктивных требований и технологических возможностей изготовления. При этом выбирают стандартные поля допусков предпочтительного применения. Способ равных допусков прост, но поскольку корректировка допусков составляющих звеньев произвольна, он недостаточно точен.

Способ допусков одного квалитета применяют, если все составляющие цепь размеры могут быть выполнены с допуском одного квалитета и допуски составляющих размеров зависят от их номинального значения. При решении задач этим способом условно принимают, что возрастание допуска линейных размеров при возрастании номинального размера имеет ту же закономерность, что и возрастание допуска диаметра. Эта закономерность выражена формулой для единицы допуска i . Для размеров от 1 до 500 мм

i=0,453 D + 0,001D ,где D – средний геометрический размер для интервала диаметров, к которому относится данный линейный размер. Таким образом, в общем виде имеем

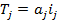,где a j – число единиц допуска, содержащееся в допуске данного размера.

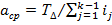зная что допуск размера замыкающего звена равен сумме допусков размеров составляющих звеньев, получаем . Величины, стоящие в знаменателе, выбирают по таблицам, величинаTзадана по условиям задачи. Величина aср , полученная по формуле, путем сравнения с табличными величинами показывает, по какому примерноквалитету следует обрабатывать размеры, составляющие цепь. Допуски выбирают из таблицы допусков на диаметры. Определив допуски, находят значения и знаки верхних и нижних отклонений составляющих размеров.

Поиск по сайту: