 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Найпростіші рухи твердого тіла
4.1.1. Поступальний рух твердого тіла. Поступальним називається такий рух твердого тіла, при якому довільна пряма або її частина, проведені в цьому тілі, залишається в процесі руху паралельною сама собі. Поступальний рух здійснюють кузов автомобіля на горизонтальній ділянці дороги, спарники коліс локомотива, педалі велосипеда. Кінематика поступального руху твердого тіла визначається такою теоремою: всі точки твердого тіла при поступальному русі мають однакові кінематичні характеристики (швидкості, прискорення і траєкторії).
 та та 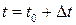 . Виберемо в тілі дві довільні точки . Виберемо в тілі дві довільні точки  які в моменту часу які в моменту часу 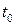 визначаються радіус-векторами визначаються радіус-векторами 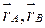 . Позначимо через . Позначимо через 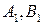 образи точок образи точок  в момент часу в момент часу 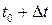 при поступальному русі (рис. 4.1). За означеннями твердого тіла і поступального руху можна записати при поступальному русі (рис. 4.1). За означеннями твердого тіла і поступального руху можна записати
Це означає, що чотирикутник
Рис. 7.1. Поступальний рух твердого тіла
Поділивши останю векторну рівність на
На підставі означення вектора швидкості матеріальної точки одержимо

Диференціюючи (4.2) по часу
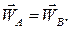
На підставі (4.1) можна записати
Остання рівність показує, що траєкторію точки Оскільки точки На підставі доведеної теореми поступальний рух твердого тіла повністю визначається рухом довільної його точки. Це означає, що задача кінематики поступального руху твердого тіла зводиться до задачі кінематики матеріальної точки (розділ 3).
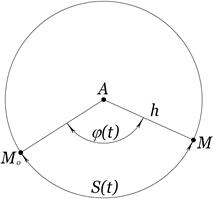
4.1.2. Обертальний рух твердого тіла навколо нерухомої осі. Розглянемо тверде тіло і деяку нерухому вісь Обертальним рухом твердого тіла навколо нерухомої осі називається такий рух, при якому кожна його точка рухається по колу, центр якого належить осі обертання
Для визначення положення тіла, що здійснює обертальний рух, проведемо через вісь обертання дві півплощини: одну нерухому, а іншу рухому, яка проходить через точки тіла і обертається разом з ним. Тоді положення тіла в довільний момент часу буде визначатися положенням рухомої півплощини, або кутом між рухомою і нерухомою півплощинами (рис. 4.2). Кут Оскільки положення твердого тіла в просторі однозначно визначається положенням трьох неколінеарних його точок, то в розглядуваному русі достатньо визначити положення довільної точки
Тому
Останні співвідношення показують, що
Розглянемо два моменти часу Середньою кутовою швидкістю точки
Границя цього відношення при
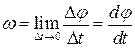 . .
Одиниця виміру кутової швидкості рад/с. Кутова швидкість є функція часу
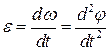 . .
Одиниця виміру кутового прискорення рад/с2. Оскільки кут повороту Зауважимо, що в залежності від напрямку обертання кутова швидкість Якщо Лінійні швидкості і прискорення точок при обертальному русі тіла. Нехай обертальний рух твердого тіла навколо нерухомої осі задано рівнянням
Розглянемо в тілі довільну точку
Тому на підставі (3.20) одержимо такі кінематичні формули для визначення швидкості і прискорення точки
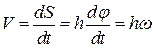 ; ; 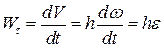 ; ; 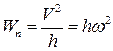 . .
Додатні напрямки швидкості і прискорення точки у випадку прискореного руху показано на Якщо рух сповільнений, то вектор
 . .
На підставі (4.7) (4.8) можна зробити висновок, що лінійні швидкості і прискорення точок тіла при його обертальному русі змінюються вздовж радіуса за лінійним законом. За цими ж формулами можна знайти рух будь-якої іншої точки, знаючи рух однієї точки тіла, а також характеристики руху всього тіла в цілому. 4.1.3. Рівнозмінний обертальний рух твердого тіла. Рух твердого тіла навколо нерухомої осі називається рівнозмінним, якщо в кожен момент часу
Інтегруючи останню рівність, будемо мати
Тут Підставляючи (4.9) в (4.6) після інтегрування, знаходимо
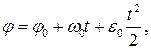
де
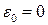 , то одержимо відповідні співвідношення для рівномірного обертального руху навколо нерухомої осі , то одержимо відповідні співвідношення для рівномірного обертального руху навколо нерухомої осі
Ці формули мають таку структуру, як і формули (3.17), (3.18). 4.1.4. Векторні формули для швидкості і прискорення точки при обертальному русі тіла.
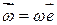 , де , де  – кутова швидкість обертального руху тіла. Його будемо називати вектором кутової швидкості. Це ковзний вздовж осі обертання вектор, напрямок якого визначається за правилом гвинта. – кутова швидкість обертального руху тіла. Його будемо називати вектором кутової швидкості. Це ковзний вздовж осі обертання вектор, напрямок якого визначається за правилом гвинта.
Диференціюючи рівність
або
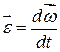 . .
Вектор
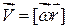 . .
Диференціюючи останню рівність по часу, знаходимо
або
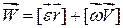 . .
Перший доданок у правій частині (4.14) визначає вектор тангенціального прискорення
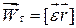 ; ; 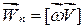 . .
Поиск по сайту: |
 .
. паралелограм, тому
паралелограм, тому 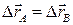 .
.
 і перейшовши до границі при
і перейшовши до границі при 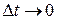 , маємо
, маємо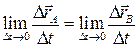 .
. , знаходимо з врахуванням (3.10)
, знаходимо з врахуванням (3.10)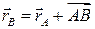 .
. можна сумістити з траєкторією точки
можна сумістити з траєкторією точки  паралельним перенесенням на вектор
паралельним перенесенням на вектор 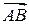 .
. При поступальному русі спільну для всіх точок тіла швидкість
При поступальному русі спільну для всіх точок тіла швидкість  називають швидкістю поступального руху тіла, а прискорення
називають швидкістю поступального руху тіла, а прискорення  – прискоренням поступального руху. Вектори
– прискоренням поступального руху. Вектори  , яка незмінно з ним зв’язана. Вважаємо, що вісь закріплена за допомогою підшипника
, яка незмінно з ним зв’язана. Вважаємо, що вісь закріплена за допомогою підшипника  З означення випливає, що довільна пряма, яка належить тілу і паралельна осі обертання описує в процесі руху кругову циліндричну поверхню. При цьому всі точки цієї прямої мають однакові швидкості, прискорення і траєкторії. Точки осі обертання залишаються нерухомими.
З означення випливає, що довільна пряма, яка належить тілу і паралельна осі обертання описує в процесі руху кругову циліндричну поверхню. При цьому всі точки цієї прямої мають однакові швидкості, прискорення і траєкторії. Точки осі обертання залишаються нерухомими.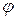 будемо називати кутом повороту тіла і вважати додатнім якщо він відкладений від нерухомої півплощини в напрямку протилежному ходу годинникової стрілки. Кут повороту вимірюється в радіанах .
будемо називати кутом повороту тіла і вважати додатнім якщо він відкладений від нерухомої півплощини в напрямку протилежному ходу годинникової стрілки. Кут повороту вимірюється в радіанах . , яка не належить осі обертання.
, яка не належить осі обертання.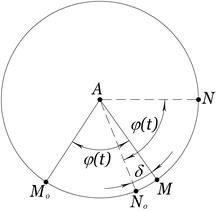 Розглянемо переріз тіла площиною, яка проходить через точку
Розглянемо переріз тіла площиною, яка проходить через точку 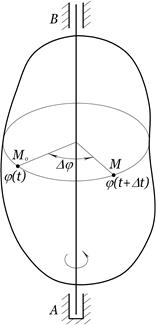



 положення точки
положення точки  . Положення точки
. Положення точки  , яка визначає закон обертального руху твердого тіла навколо нерухомої осі. Зауважимо, що кут
, яка визначає закон обертального руху твердого тіла навколо нерухомої осі. Зауважимо, що кут  буде однаковим для всіх точок розглядуваного кола (рис. 4.3), отже і для всіх точок тіла. Це випливає із означення абсолютно твердого тіла, для якого
буде однаковим для всіх точок розглядуваного кола (рис. 4.3), отже і для всіх точок тіла. Це випливає із означення абсолютно твердого тіла, для якого .
.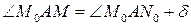 і
і  .
.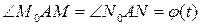 .
.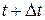 , яким відповідає два положення точки
, яким відповідає два положення точки 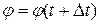 . Приріст кута повороту точки
. Приріст кута повороту точки 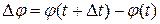 (рис. 4.4).
(рис. 4.4).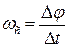 .
.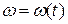 . Похідна від неї по часу називається кутовим прискоренням точки
. Похідна від неї по часу називається кутовим прискоренням точки  будемо називати відповідно кутовою швидкістю і кутовим прискоренням твердого тіла.
будемо називати відповідно кутовою швидкістю і кутовим прискоренням твердого тіла.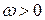 тіло обертається в додатному напрямку.
тіло обертається в додатному напрямку. , то обертальний рух твердого тіла називається прискореним, при
, то обертальний рух твердого тіла називається прискореним, при  – сповільненим.
– сповільненим. (рис. 4.5).
(рис. 4.5). .
.
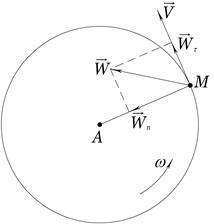

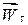 змінює напрямок на протилежний. Повне прискорення точки
змінює напрямок на протилежний. Повне прискорення точки 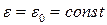 . За формулою (4.6) знаходимо
. За формулою (4.6) знаходимо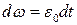 .
. ,
,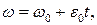
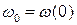 – початкова кутова швидкість тіла.
– початкова кутова швидкість тіла.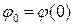 – початковий кут повороту тіла.
– початковий кут повороту тіла.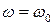 ;
;  .
.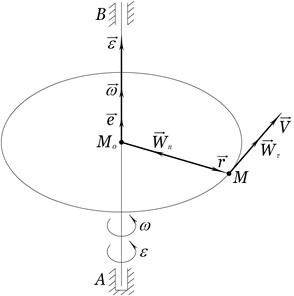 Розглянемо тверде тіло, яке здійснює обертальний рух навколо нерухомої осі за законом
Розглянемо тверде тіло, яке здійснює обертальний рух навколо нерухомої осі за законом 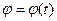 . Всі точки тіла в кожний момент часу мають однакові величини
. Всі точки тіла в кожний момент часу мають однакові величини 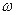 і
і 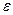 . Вісь обертання
. Вісь обертання 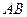 в процесі руху залишається незмінною, тому її додатній напрямок можна визначити одиничним вектором
в процесі руху залишається незмінною, тому її додатній напрямок можна визначити одиничним вектором 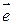 за правилом гвинта (рис. 4.7).
за правилом гвинта (рис. 4.7).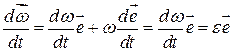 ,
,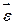 називається вектором кутового прискорення обертального руху тіла. Якщо
називається вектором кутового прискорення обертального руху тіла. Якщо 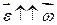 і такий обертальний рух називається прискореним. При
і такий обертальний рух називається прискореним. При 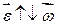 – обертальний рух називається сповільненим. Введення векторів
– обертальний рух називається сповільненим. Введення векторів  та
та 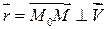 і
і 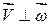 , то за означенням векторного добутку двох векторів можна записати
, то за означенням векторного добутку двох векторів можна записати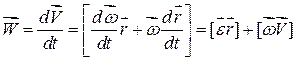 ,
, . При цьому
. При цьому