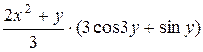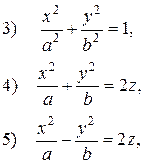|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Форматирование трехмерных графиков
Форматирование трехмерных графиков выполняется с помощью диалогового окна Форматирование 3-D графика (3-D Plot Format), которое вызывается двойным щелчком мыши в области графика. В этом диалоговом окне доступно большое количество параметров, изменение которых способно очень сильно повлиять на внешний вид графика (см. рис. 9, 10). Они сгруппированы по принципу действия на нескольких вкладках. Изменение типа графика Чтобы поменять тип уже имеющегося графика необходимо установить соответствующий переключатель в нижней части вкладки Общие (General) и нажать кнопку ОК. График будет перерисован. Вращение графика Самый простой способ ориентации системы координат с графиком в трехмерном пространстве это перетаскивание ее указателем мыши. Другой способ изменения ориентации графика – с помощью полей Вращение (Rotation), Наклон (Tilt) и Искривление (Twist) на вкладке Общие (General), которые в совокупности определяют соответствующие углы и тем самым задают направление всех трех осей координат в пространстве. Стиль осей С помощью группы переключателей можно задать один из следующих стилей оси координат: · Периметр (Perimeter); · Угол (Corner); · Нет (None) – оси отсутствуют. Масштабирование графика В поле Масштаб (Room) вкладки Общие (General) можно задать числовое значение масштаба. Формирование осей Вкладка Оси (Axes) содержит три вложенных вкладки, в которых задаются параметры для каждой из трех координатных осей. Стиль заливки и линий Задать различный стиль заливки и линий можно с помощью вкладки Внешний вид (Appearance) для контурного и поверхностного графиков. При выборе переключателя Залить поверхность (Fill Surface) из группы Параметры заливки (Fill Options) вы получаете доступ к опциям цвета (Color Options). Если выбрать переключатель Сплошной цвет (Solid Color), то получится однотонная заливка поверхности. Если установить переключатель Палитра (Colormap), то поверхность или контурный график будут залиты разными цветами и оттенками, при чем выбрать цветовую схему можно на вкладке Дополнительно (Advanced). Спецэффекты На вкладке Дополнительно (Advanced) имеется доступ к управлению несколькими специальными эффектами оформления графиков, благодаря которым они смотрятся более красиво. К эффектам относятся: · Блеск (Shininess) – имеется возможность регулировать сияние в пределах от 0 до 128; · Туман (Fog) – эффект тумана; · Прозрачность (Transparency) – задается процент прозрачности графика; · Перспектива (Perspective) – показ перспективы с определением видимости расстояния. Заголовок графика Заголовок графика определяется на вкладке Название (Title) и может быть расположен как сверху, так и снизу графика. Редактирование точек данных Формат точек, включая тип символа, размер, соединение их линий задается на вкладке Внешний вид (Appearance). Задание по теме №5_1
I. Построить поверхности:
1) z(x, y)=2×x×sinx+3×y×cosy
2)
Лабораторная работа №6.
Изучая иеорию интерполяции, вы познакомились с интерполяционными формулами, которые в точности воспроизводят значения данной функции в узлах интерполяции. Однако в ряде случаев выполнение этого условия затруднительно или даже нецелесообразно: 1. Если заданные величины х и у являются экспериментальными данными, то могут содержать в себе существенные ошибки, т.к. получены в результате измерений или наблюдений. Поэтому построение аппроксимирующего многочлена, воспроизводящего в точности заданное значение функции, означало бы тщательное копирование допущенных при измерениях ошибок. 2. Если имеются точные значения функции в некоторых точках, но число таких точек n весьма велико, то интерполяционный многочлен будет очень высокой степени (если только разности не будут становиться постоянными). Поэтому возникает задача построения многочлена некоторой вполне определенной степени, но меньшей чем n - 1, который хотя и не дает точных значений функции в узлах интерполяции, но достаточно близко к ним подходит.
Поиск по сайту: |