 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Численное интегрирование и дифференцирование
Наиболее распространенным подходом к численному вычислению интеграла
является разбиение отрезка [a, b] на n равных частей а = х0< х1< . . . < хn = b c шагом h =
Соотношения вида (2) называют квадратурными формулами. Численное интегрирование с помощью ортогональных полиномов
Численное дифференцирование аналитически или таблично заданной функции f(x) на отрезке [a, b] в точке х = Х заключается в замене f(x) интерполяционным полиномом ϕ(x),
Для численного вычисления интеграла
отрезок [a, b] разбивают на n равных частей а = х0< х1< . . . < хn = b c шагом h =
В простейших случаях в качестве интерполяционного многочлена ϕ(x) берут ступенчатую, кусочно-линейную или кусочно-параболическую функции, а также полином степени k = n (ϕ(x) = xk).
Рис. 2. Численное дифференцирование и интегрирование
Разные методы интегрирования формула прямоугольников
формула трапеций
формула Симпсона (n – четное число)
Символьное интегрирование и дифференцирование Для вычисления интегралов (или нахождения первообразных) аналитически заданной функции используется команда Symbolic →Integrateon Variable(Интегрировать по переменной). Она возвращает символьное значение неопределенного интеграла по указанной маркером ввода переменной. Выражение, в состав которого входит переменная, является подынтегральной функцией. Команда Symbolic→Differentiate on Variable(Дифференцировать попеременной) возвращает символьное значение производной выражения по той переменной, которая указана курсором. Для вычисления производных высшего порядка нужно повторить вычисление необходимое число раз. Результат символьного преобразования иногда содержит специальные функции, которые не являются частью списка встроенных функций MathCAD. Вот определения некоторых из них: γ – константа Эйлера,
Дифференцирование
С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов до 5-го порядка включительно. И функции, и аргументы могут быть как действительными, так и комплексными.
Поиск по сайту: |
 (1)
(1)
 , интерполирование функции y = f(x) на отрезке [a, b] (получение интерполяционного многочлена Φ(x)) и замена в (1) интеграла интегральной суммой:
, интерполирование функции y = f(x) на отрезке [a, b] (получение интерполяционного многочлена Φ(x)) и замена в (1) интеграла интегральной суммой: (2)
(2)
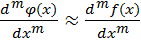 который можно найти аналитически с помощью соответствующих формул
который можно найти аналитически с помощью соответствующих формул (7).
(7). (5)
(5) (6).
(6).


 мМетод неопределенных коэффициентов состоит в вычислении определенного и интеграла (1) с помощью формулы (2), коэффициенты Аi, которой находятся в
результате решения следующей системы уравнений:
мМетод неопределенных коэффициентов состоит в вычислении определенного и интеграла (1) с помощью формулы (2), коэффициенты Аi, которой находятся в
результате решения следующей системы уравнений:
 Г где
Г где  , k = 0, 1, . . ., n.
, k = 0, 1, . . ., n.

