 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Мультипликатор автономных налогов
Рассмотрим сначала действие мультипликатора автономных налогов, т.е. не зависящих от уровня дохода. Поскольку в простой кейнсианской модели предполагается, что налоги взимаются только с домохозяйств, т.е. оказывают влияние на величину потребительских расходов, то с включением в наш анализ налогов меняется функция потребления, принимая вид: С = С + mрc (Y – Т). Изменение налогов ведет к изменению величины располагаемого дохода. (РД = ЛД – Т). Рост налогов сокращает располагаемый доход, а сокращение налогов - увеличивает располагаемый доход. Если, например, налоги сокращаются на 100$, то располагаемый доход увеличивается на 100$. Но располагаемый доход делится на потребление (С) и сбережения (S). Если мрc = 0.8, то при увеличении располагаемого дохода на 100$ потребление увеличивается на 80$ (100 х 0.8= 80), а поскольку мультипликатор расходов в этом случае равен 5 (1/(1 – 0.8) = 1/0.2 = 5), то прирост совокупного дохода в результате изменения налогов на 100$ составит 400$ (DY = DС х 1/(1- мрc) = 80 х 5 = 400), а не 500$, как в случае изменения государственных закупок на те же 100$, т.е. мультипликативный эффект меньше. Т.е. мультипликатор начинает действовать как бы со второй ступени (первым членом геометрической прогрессии будет не 100, а 80). Определим теперь величину мультипликатора налогов. Налоги действуют на совокупный спрос через изменение потребительских расходов.
Подставив формулу (2) в формулу (1) и несколько перегруппировав, получим:
Величина Выведем мультипликатор автономных налогов алгебраически. Подставим функцию потребления: Следует обратить внимание на 2 момента: 1) мультипликатор налогов всегда величина отрицательная. Это означает, что его действие на совокупный доход обратное. Рост налогов приводит к снижению совокупного дохода, а сокращение налогов – к росту совокупного дохода. В нашем примере сокращение налогов на 100$ (Т= - 100) привело к увеличению совокупного дохода на 400$ (Y = - mрc /(1 – mрc) х (Т) = - 0.8/(1 – 0.2) х 100 = - 4 х (-100) = 400) 2) по своему абсолютному значению мультипликатор налогов всегда меньше мультипликатора автономных расходов. Итак, мультипликативный эффект налогов меньше, чем мультипликативный эффект государственных закупок (очевидно, что [mрc mрc)] < [1 / (1 - mрc)]), поскольку изменение государственных закупок воздействует на совокупный спрос непосредственно (они включены в формулу совокупного спроса), а изменение налогов воздействует косвенно – через изменение потребительских расходов. Например, если при mрс = 0.8 и государственные закупки, и налоги увеличиваются на 100$, то рост государственных закупок увеличивает совокупный доход на 500$ (Y = G х 1/(1 – mрс) = 100 х 5 = 500), а рост налогов сокращает совокупный доход на 400$ (Y = Т х [-mрс /(1 – mрс)] = 100 х (- 4) = 400). Т.е. в результате совокупный доход (выпуск) увеличился на $100. Исходя из этого обстоятельства, можно вывести мультипликатор сбалансированного бюджета для автономных (аккордных) налогов.
Поиск по сайту: |
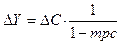
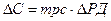
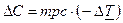
Þ 
и есть мультипликатор налогов. А поскольку (1 – mрc) есть не что иное, как mрs (предельная склонность к сбережению), то мультипликатор налогов можно записать и как (-mрc / mрs). В нашем примере он равен (- 4) (- 0.8 / (1 - 0.8) = - 0.8 / 0.2 = - 4). Мультипликатор налогов – это коэффициент, который показывает, во сколько раз увеличится (сократится) совокупный доход при сокращении (увеличении) налогов на единицу.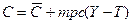
в функцию национального дохода Y= С + I + G, получим: Y = С + mрc (Y – Т) + I + G, откуда 
. Если обозначить мультипликатор автономных налогов КТ, то 
и, следовательно DY = КТ DТ