 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Эффект мультипликатора
Для того, чтобы определить величину равновесного выпуска (равновесного национального дохода) следует приравнять его к величине планируемых расходов: Что произойдет, если увеличатся расходы? Кейнс показал, что рост расходов ведет к росту дохода, однако доход возрастает в большей степени, чем вызвавшее его увеличение расходов, т.е. с эффектом мультипликатора. Мультипликатор – это коэффициент, который показывает, во сколько раз увеличивается (сокращается) совокупный доход (выпуск) при увеличении (сокращении) расходов на единицу. Действие мультипликатора основано на том, что расходы, сделанные одним экономическим агентом обязательно превращаются в доход другого экономического агента, который часть этого дохода расходует, создавая доход третьему агенту и т.д. В результате общая сумма доходов будет больше, чем первоначальная сумма расходов. Предположим, что домохозяйство увеличивает свои автономные расходы на $100, т.е. покупает на эту сумму товары и услуги. Это означает, что производитель этих товаров и услуг получает доход в $100, который он тратит на потребление и сбережения. Предположим, что предельная склонность к потреблению мрс = 0.8, что означает, что из каждого дополнительного 1 доллара дохода экономический агент тратит на потребление 80 центов (т.е. 80%), а 20 центов (т.е. 20%) сберегает (т.е. предельная склонность к сбережению mрs = 0.2 ). В этом случае, получив $100 дополнительного дохода, производитель потратит $80 на потребление (Y х mрс =100 х 0.8 = 80) и $20 пойдут на сбережения (Y х mрs = 100 х 0.2 = 20). Потраченные им на потребление (на покупку товаров и услуг) $80 создадут дополнительный доход еще одному продавцу, который в свою очередь потратит $64 на потребление (Y х mрс = 80 х 0.8 = 64) и $16 сбережет (соответственно 80 х 0.2 = 16) и т.д. Процесс будет продолжаться до тех пор, пока прирост расходов не дойдет до 0.
Просуммируем все полученные доходы, чтобы узнать, насколько в результате увеличился совокупный доход:
Аналогичные рассуждения применимы и к изменению (автономных) инвестиционных расходов. Увеличивая инвестиции, фирма закупает инвестиционные товары, создавая доход их производителю, который в свою очередь расходует часть этого дохода на потребление, обеспечивая доход производителю этих потребительских товаров и т.д. В результате рост совокупного дохода будет в несколько раз большим, чем первоначальный прирост инвестиций, т.е. будет действовать эффект мультипликатора, и мультипликатор (но в данном случае инвестиционных расходов) также будет равен Формулу мультипликатора автономных расходов можно вывести и алгебраически. Поскольку:
Графическое изображение эффекта мультипликатора расходов (например, мультипликатора инвестиций) представлено на рис.9.5.
Чем выше предельная склонность к потреблению (mрс), тем величина мультипликатора автономных расходов больше. Так, например, если mрс = 0.9, мультипликатор = 10 (1 / (1 – 0.9) = 10), а при mрс = 0.75, мультипликатор = 4 (1 / (1 – 0.75) = 4). А поскольку mрс определяет наклон кривой планируемых расходов, то чем больше mрс, тем кривая более крутая.
А чем более крутая кривая планируемых расходов (т.е. чем больше mрс и, следовательно, мультипли-катор, тем больший при-рост дохода даст одинаковое увеличение расходов). Это проиллюстрировано на рис.9.6. На рис.9.6 (б) предельная склонность к потреблению (mрс) больше, а поэтому кривая планируемых расходов более крутая и мультипликативный эффект роста дохода при одинаковой величине роста расходов больше (DY2 > DY1), чем на рис.9.6 (а).
Поиск по сайту: |
 , где
, где  , то есть
, то есть  .
.
 Мы получили бесконечно убывающую геометрическую прогрессию (а это и есть математический смысл мультипликатора) с основанием (mрс) меньше единицы. Следовательно, ее сумма равна
Мы получили бесконечно убывающую геометрическую прогрессию (а это и есть математический смысл мультипликатора) с основанием (mрс) меньше единицы. Следовательно, ее сумма равна  , т.е.
, т.е.  . Выражение
. Выражение 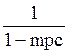 представляет собой мультипликатор (автономных)потребительских расходов. В нашем примере мультипликатор равен 5 (1 / 1 – 0.8 = 5). Следовательно, при росте автономных потребительских расходов на $100 рост совокупного дохода составил $500 (100 х 5 = 500).
представляет собой мультипликатор (автономных)потребительских расходов. В нашем примере мультипликатор равен 5 (1 / 1 – 0.8 = 5). Следовательно, при росте автономных потребительских расходов на $100 рост совокупного дохода составил $500 (100 х 5 = 500). .
.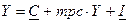


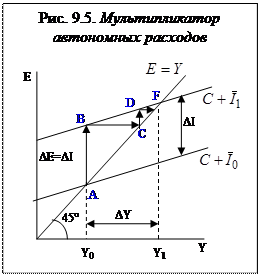 На рисунке видно, что каждый следующий прирост дохода меньше, чем предыдущий. Процесс мультипликации длится до тех пор, пока прирост дохода не станет равным нулю.
На рисунке видно, что каждый следующий прирост дохода меньше, чем предыдущий. Процесс мультипликации длится до тех пор, пока прирост дохода не станет равным нулю.