|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Процесс заряда конденсатора от источника постоянного напряжения
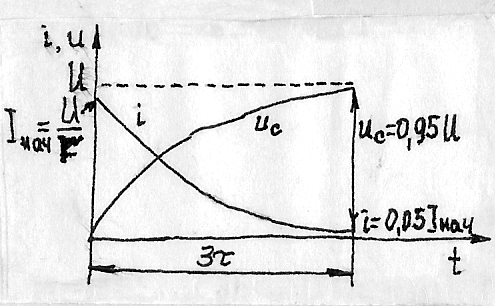
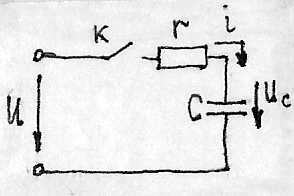
Заряд емкости через сопротивление а) схема; б) эпюры напряжений
После замыкания ключа К начинается заряд конденсатора с и в цепи протекает ток заряда i. По II закону Кирхгофа: ir+uc –u=0; отсюда i=u-uc/r ; В то же время i= c duc/dt Приравняв выражение для токов, имеем: uc=rc* duc/dt +uc Решение этого дифференциального уравнения:
где τ=rc – постоянная времени цепи [Ом*с/Ом ] =[с]
Нарастание напряжения на емкости до 95%. Остальные максимальные значения n стадий тока до 5% от начального значения происходит по экспоненте за время t=3τ, т. е. процесс заряда инерционен и зависит от параметров цепи. Рассмотрим цепь, в которой конденсатор подключен к источнику синусоидальной ЭДС.
а) схема б) временный график В первую четверть периода напряжение uc возрастает, du/dt>0 , i>0; при этом положительные направления i и uc совпадают, энергия источника переходит в энергию поля конденсатора, который накапливает энергию Wc =(cucm ) 2 /2. Во вторую четверть периода напряжение убывает, du/dt<0 , i<0; ток изменяет направление, и энергия поля конденсатора возвращается в источник. В следующую половину периода ток изменяет, и процесс накопления и возврата энергии конденсатором повторяется. Следовательно, в цепи с идеальной емкостью (при отсутствии активных потерь) происходит непрерывный обмен энергией между источником и полем конденсатора без потерь. Соединение конденсаторов
Параллельное соединение конденсаторов. Здесь конденсаторы находятся под общим напряжением u, а общий заряд, который они получают от источника:
Поэтому Параллельное соединение конденсаторов применяют для увеличения общей емкости.
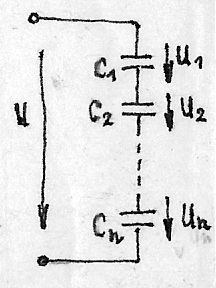
В этом случае заряды, получаемые конденсаторами, одинаковы, т.к. через них протекает один и тот же ток.
Поэтому: C3=q/u1+u2+...+un=q/(q/C1)+(q/C2)+...+(q/Cn)=1/(1/C1)+(1/C2)+...+(1/Cn) Если С1=С2=…=Сn ; то С3=С/n . Последовательное соединение конденсаторов применяют в случае, когда допустимое напряжение одного конденсатора меньше напряжения источника. Индуктивный элемент
Индуктивный элемент в цепи синусоидального тока характеризуется наличием изменяющегося магнитного поля, создаваемого этим током, интенсивность которого может быть оценена магнитным потоком Ф, выражаемым в веберах [Вб] или [В*с]
Сумма магнитных потоков отдельных витков катушки индуктивности называется потокосцеплением.
где: W – количество витков катушки индуктивности; Если магнитные потоки всех витков одинаковы, то
С другой стороны, потокосцепление:
где L – индуктивность, представляющая собой в данном случае коэффициент пропорциональности между потокосцеплением и током, вызывающим его:
Единица индуктивности – генри; дольные единицы милли-, микрогенри [мГн], [мкГн]. Наведение ЭДС в катушке индуктивности при изменении потокосцепления называется самоиндукцией. Согласно закону электромагнитной индукции ЭДС самоиндукции определяется скоростью изменения потокосцепления, взятая с обратным:
Следовательно, индуктивность может быть также определена как коэффициент пропорциональности между скоростью изменения тока в катушке и наводимой при этом ЭДС самоиндукции. Знак «-» означает, что ЭДС самоиндукции препятствует причине, вызывающей её.
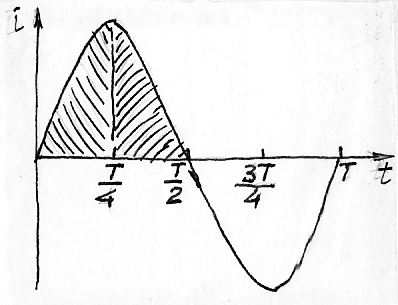
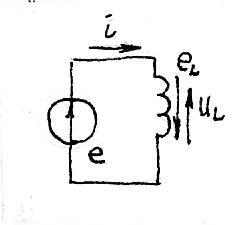
Работа катушки индуктивности в цепи синусоидального тока: а) схема б) временный график Действительно, если катушку индуктивности подключить к источнику синусоидальной ЭДС, то: В первую четверть периода ток возрастает (di/dt>0) и ЭДС самоиндукции еl<0, направлена навстречу току и препятствует его увеличению.
Во вторую четверть периода ток убывает (di/dt<0) и ЭДС самоиндукции еl>0, т. е. совпадает с направлением тока, препятствуя его уменьшению; При этом энергия магнитного поля катушки возвращается в источник. Следовательно, в цепи с идеальной катушкой индуктивности (т.е. при отсутствии активных потерь) происходит непрерывный обмен энергией между источником и магнитным полем катушки без потерь. Напряжение на катушке индуктивности равно по величине и противоположено по направлению ЭДС индукции: ul=-el Рассмотрим процесс увеличения силы тока в цепи с индуктивностью и активным сопротивлением при подключении постоянного напряжения.
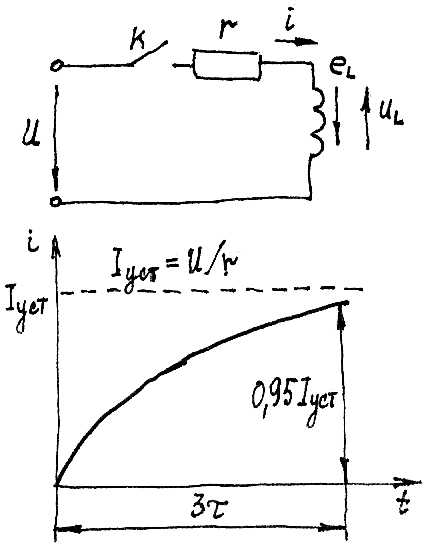
Увеличение силы тока в цепи, содержащей индуктивность и активное сопротивление: а) схема; б) временный график
При замыкании ключа К в цепи начинает протекать ток. Составим уравнение по II закону Кирхгофа для данной цепи: ir-el-u=0; i=u+ei/r; el=-L di/dt; u=ir+L di/dt. Решение этого дифференциального уравнения имеет вид:
Iуст=u/r – установившийся ток по окончании переходного процесса. τ=L/r [Ом*с/Ом]= [с] - постоянная времени цепи. Из временного графика видно, что нарастание тока до 95% установившегося значения Iуст=u/r происходит по экспоненте за время t=3 τ. Спад тока в цепи до 5% от установившегося значения также происходит по экспоненте за время t=3 τ. Лекция №5
Поиск по сайту: |


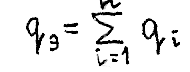
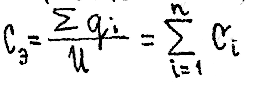
 Последовательное соединение конденсаторов.
Последовательное соединение конденсаторов.


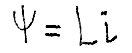
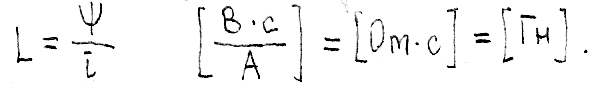
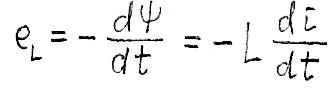
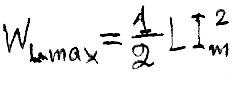 При этом энергия источника переходит в энергию магнитного поля катушки:
При этом энергия источника переходит в энергию магнитного поля катушки: