|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод эквивалентного генератора.
Пусть требуется определить ток
Воспользуемся методом суперпозиции
Если
Где
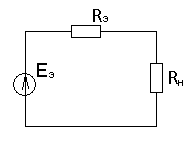
Метод эквивалентного генератора позволяет определить ток только в одной ветви эл. схемы кроме этой ветви активным двухполюсником (эквивалентным генератором ЭДС) с сопротивлением
При этом согл. теореме об эквивалентном генераторе. Должно выполняться условие для этих двух равенств хотя бы двух из трех параметров относительно зажимов, где включен По второму закону Кирхгофа
Следовательно,
Для расчета тока в отдельной ветви необходимо определить Последовательность расчета методом эквивалентного генератора.
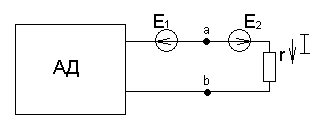
а) б) в) Рис.1.31 2.
Пусть требуется определить ток 3. Условно исключаем из цепи участок, на котором требуется определить ток, оставляя его разомкнутым (создаем режим х.х. в этой цепи (рис.1.31,б)). 4. Выбираем произвольно и обозначаем на схеме положительное направление 5. Определяем
Примечание: если в результате решения 6. Указываем на схеме если это необходимо, действительное направление 7. Мысленно исключаем из схемы источник (оставляя их внутренние сопротивления) и определяем
8. Определяем ток в исследуемой цепи (ветви):
Направления тока совпадает с направлением Метод эквивалентного генератора (активного двухполюсника) позволяет достаточно просто рассчитать отдельный участок эл. цепи а также преобразовать (упростить) цепь, заменив ее эквивалентной схемой. Лекция №3 1.1.14. Баланс мощности в цепях постоянного тока. В общем виде уравнение баланса мощности имеет вид:
Где m, n – количество источников и приемников соответственно. Определение: условия баланса мощности. Алгебраическая сумма мощностей, вырабатываемых источниками, равна арифметической сумме мощностей, которые потребляют приемники и вспомогательные элементы (т.к. в правую часть уравнения входит квадрат тока, т.е. его направление не имеет значения; поэтому сумма арифметическая). В левой части уравнения возможны следующие случаи: - При совпадении по направлению в активной ветви ЭДС и тока слагаемым присваивается знак «+» (т.е. источник отдает энергию в цепь); - Если направление ЭДС и тока противоположны, слагаемым присваивается знак «-» (т.е. источник работает в режиме приемника). 1.1.15.Способы соединения источников электрической энергии. А. Последовательное соединение источников Рис.1.32.
Пусть имеется n последовательно соединенных источников Для этих цепей составим уравнение по второму закону Кирхгофа
Приравняем выражения для
Где
Последовательное соединение источников позволяет увеличивать напряжение, действующее на нагрузке. Б. Параллельное соединение источников.
Рис.1.33. Пусть имеется n- параллельно соединенных источников
В режиме холостого хода
Если
Приравниваем выражения для
И подставим в это неравенство выражение (1.10) для
Отсюда следует, что Параллельное соединение источников применяют тогда, когда номинальный ток и мощность одного источника недостаточны для питания приемников:
1.1.16. Условие передачи максимальной мощности источника во внешнюю цепь.
Рис.1.34. Рассмотрим цепь (рис.1.34.), в которой
Мощность в нагрузке
В режиме к.з.: В режиме х.х.: Т.к. при крайних значениях
Для определения экстремума продифференцируем данную дробь и приравняем производную к нулю.
(
Таким образом, мощность, отдаваемая источником в нагрузку, максимальная, когда внутреннее сопротивление источника равно сопротивлению нагрузки. Такой режим называется согласованным.
Где
При х.х. : При к.з. : Согласованный режим:
Рис.1.35. Зависимости
Лекция №4 Основные понятия о синусоидальном переменном токе. Переменный ток используется в различных областях электротехники. Электрическая энергия в промышленной энергетике почти во всех случаях производится, распределяется и потребляется в виде энергии переменного тока. Это объясняется тем, что переменный ток легко трансформировать, преобразовывая переменный ток высокого напряжения в переменный ток низкого напряжения и наоборот. Переменным током (напряжением) называется такой ток (напряжение), который периодически во времени изменяет своё значение и направление. Закон изменения тока (напряжения, ЭДС) во времени может быть любым. Однако в промышленной энергетике используется преимущественно ток (напряжение, ЭДС) изменяющийся по гармоническому закону. При этом обеспечивается наиболее простой механизм получения синусоидальной ЭДС (модель – рамка, вращающаяся с постоянной угловой скоростью ω в равномерном магнитном поле), достигается максимальной КПД генераторов, двигателей и трансформаторов. Возникающая в катушках индуктивности ЭДС самоиндукции e= -L di/dt и ток через конденсаторы i=C duc/u также изменяются по закону, что невозможно при любой другой функции. При этом существенно упрощается расчёт электрических цепей. Мгновенные значения ЭДС, тока и напряжения: e=Emsin(ωt+Ψe) i=Imsin(ωt+Ψi) u=umsin(ωt+Ψu) где um ,Im ,Em - максимальное (амплитудное) значение ЭДС тока, напрямую полученное при sin(ωt+Ψe)=1 т. е. (ωt+Ψe)=π/2. ω=2πƒ – условная частота, рад/с ƒ=1/Т – циклическая частота, 1/с Т – период колебания. Период – это время, в течении которого совершается один цикл периодического процесса. Ψе , Ψi , Ψu – начальные фазы (при t=0). (ωt+Ψ) – текущая фаза колебания.
Временный график синусоидального тока
1.2.2 Элементы электрических цепей синусоидального тока. Одна из особенностей цепей синусоидального тока заключается в том, что в них могут присутствовать емкостные и индуктивные элементы, которые вносят фазовые сдвиги между током и напряжением; их сопротивление переменному току зависит от частоты. 1. Емкостный элемент.
В процессе заряда этого конденсатора на его обкладках накапливаются заряды противоположенного знака. q=cu , где с – емкость конденсатора.
Таким образом, емкость – это коэффициент пропорциональности между приложенным к конденсатору напряжением и наложенным в нём зарядом: c= q/u; Кл/В=Ас/В=с/Ом=Ф Емкость выражается в фарадах (а также в микро-, нано-, пикофарадах) Емкость плоского конденсатора с= ε ε0 S/d=εа *S/d ε0= 8,854 * 10-12 Ф/м – диэлектрическая проницаемость вакуума. ε= относительная диэлектрическая проницаемость диэлектрика. S – площадь пластин d - расстояние между пластинами/ Напряжение и ток емкостного элемента связаны уравнением: i=dq/dt=c*duc/dt; отсюда u=1/с ∫ i* dt+A где А – постоянная величина. При синусоидальном токе А=0, т.к. эта функция не имеет составляющей.
Поиск по сайту: |
 лишь в одной ветви аmв, тогда остальная часть схемы представим в виде активного двухполюсника
лишь в одной ветви аmв, тогда остальная часть схемы представим в виде активного двухполюсника

 =
= 



 таков, что
таков, что  (х.х), то
(х.х), то
 - эквивалентное сопротивление двухполюсника.
- эквивалентное сопротивление двухполюсника.




 – напряжение, создаваемое в цепи при хх, т.к.
– напряжение, создаваемое в цепи при хх, т.к.  и с учетом
и с учетом 

 можно определить расчетным и опытным путем.
можно определить расчетным и опытным путем.


 в цепи аnв(рис.1.31,а).
в цепи аnв(рис.1.31,а). (рис.1.31,б).
(рис.1.31,б).
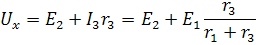
 относительно точек, откуда исключен исследуемый участок цепи (рис.1.31,в)
относительно точек, откуда исключен исследуемый участок цепи (рис.1.31,в)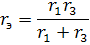

 .
.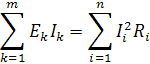

 ,
,  , которые надо заменить эквивалентной схемой с одним источником
, которые надо заменить эквивалентной схемой с одним источником 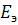 ,
,  (рис.1.32.)
(рис.1.32.)

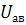 в схемах рис.1.32,а и 1.32.б и получим
в схемах рис.1.32,а и 1.32.б и получим
 – напряжение, создаваемое
– напряжение, создаваемое -м источником.
-м источником.
 которые надо заменить эквивалентной схемой с
которые надо заменить эквивалентной схемой с 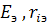 (рис.1.33). Применим для этих цепей метод узловых напряжений:
(рис.1.33). Применим для этих цепей метод узловых напряжений:


 Приравняв эти выражения для
Приравняв эти выражения для 








 может меняться от 0 до
может меняться от 0 до  ток в этой цепи
ток в этой цепи



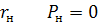 , то это значит, что существует максимум, где-то в этом промежутке, где
, то это значит, что существует максимум, где-то в этом промежутке, где


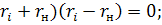 отсюда
отсюда
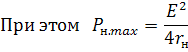

 – мощность в нагрузке
– мощность в нагрузке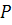 – мощность, развиваемая источником
– мощность, развиваемая источником



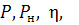 от
от