 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Анализ продольного профиля пути и выбор расчетного подъема
Анализ заданного профиля пути участка заключается в следующем: – определение станции, на которой будет проверяться критическая масса состава по условию взятия поезда с места; – установление наибольшего спуска, на котором будет решаться тормозная задача; – обоснование и выбор расчетного подъема, значение которого будет использоваться в дальнейшем при определении критической массы состава. Критическая масса состава будет определяться на станции Б, так как для проверки массы состава по троганию с места эта станция расположена на наиболее трудном элементе, уклон равен +2 ‰. При спрямлении элемента 12 (см. таблицу 3.1) установили наибольший спуск, на котором будет решаться тормозная задача. Определяем расчетный подъем, он равен +8,0 ‰, т.к. он имеет длину 5000 м, на нем находится кривая длинной 500 метров и радиусом 150 м, ему предшествует подъем +2‰ на длине 1200 метров. Также он является не самым крутым, самый крутой подъем равен +10,0 ‰ и имеет длину 900 м (см. таблицу 3.1). Поэтому на подъеме равном +8,0 ‰ при длине 5000 м может быть достигнута равномерная скорость движения.
3.2 Спрямление и приведение профиля пути
Для упрощения тяговых расчетов продольный профиль и план пути подвергаем обработке, состоящей из двух операций: 1) спрямление продольного профиля – объединение ряда его смежных элементов в один участок с однородным уклоном i'с; 2) спрямление пути в плане – замена кривых фиктивными подъемами i"с в пределах спрямленных элементов профиля. Спрямленный профиль должен сохранять особенности действительного профиля, поэтому нельзя спрямлять: – элементы профиля пути станции; – элементы с уклонами разного знака; – расчетного подъема с прилегающими элементами. Крутизну спрямленного элемента i'с, ‰, определяют по формуле
i'с =
где i1, i2, … in – уклоны спрямляемых элементов, ‰; S1, S2, … Sn – длины спрямляемых элементов, м.
Чтобы в расчетах не допустить больших погрешностей из-за замены действительного профиля спрямленным, проводят проверку допустимости их спрямления по эмпирической формуле
S j ≤ 2000 /│i'c - in│, (3.2)
где S j – длина спрямляемого элемента пути, м; ∆i – абсолютная разность между уклонами спрямленного и спрямляемого элементов, ‰. Такой проверке подвергаются все элементы, входящие в спрямляемую группу. Если хотя бы один элемент не удовлетворяет условию (3.2), то такую группу спрямлять нельзя. Если на спрямляемых элементах расположены кривые, то их заменяют фиктивным подъемом от кривой i"c, ‰, по формуле
где n – количество кривых на спрямленном участке; Sкр – длина кривой, м; Rкр – радиус кривой, м. Приведенный уклон спрямленного элемента в продольном профиле и плане пути ic, ‰, определяется по выражению
ic=i'c+i"c . (3.4)
Подставим числовые значения в заданные формулы. Числа будем брать из таблицы 1.1. Элемент 1 - станция В – этот элемент не спрямляется. Станция В не находится на кривой, приведенный уклон будет равен крутизне участка, которая равна 0,0‰. Спрямляем 2-3 элементы по формуле (3.1)
i'c=
Проводим проверку по формуле (3.2):
700 ≤ 2000/|1,6-0|
700 м < 1250 м
800 ≤ 2000/|3-1,6|
800 м < 1469,5 м
Проверка выполняется, значит можно спрямить эти два элемента. Приведенный уклон вычисляется по формуле (3.4):
ic=-1,6+0=-1,6‰.
Элемент 4 спрямлять нельзя, так как ему предшествовали площадка с уклоном, а за ним находится расчетный подъем, на котором будет определяться критическая масса состава. Приведенный уклон вычисляется по формуле (3.4):
ic=2,0+0,0=2,0‰.
Элемент 5 спрямить нельзя, так как на 5 элементе находится расчетный подъем. Элементы 4 и 5 переносим в таблицу. Элемента 5, расположен в кривой, поэтому выполняем расчет фиктивного подъема от кривой i"c, ‰, по формуле (3.3):
i"c=
Приведенный уклон вычисляется по формуле (3.4):
ic=8,0+0,5=8,5‰.
Спрямляем 6-7 элементы по формуле (3.1)
iс' =
Проводим проверку по формуле (3.2):
500 ≤ 2000/|3,4-3|
500м <5000м
500 ≤ 2000/|4-3,4|
300м < 3333,3м Проверка выполняется, значит, можем спрямить эти два элемента. Приведенный уклон вычисляется по формуле (3.4):
ic=-3,4+0,0=-3,4‰.
Элемент 8 нельзя спрямить ни с элементами 6-7, ни 9-10, так как они имеют разные знаки. Поэтому элемент 8 переносим в таблицу. Приведенный уклон, для элемента 8, вычисляется по формуле (3.4):
ic=10,0+0,0=10,0‰.
Спрямляем 9 и 10 элемент по формуле (3.1)
i'c=
Проводим проверку по формуле (3.2):
4500 ≤ 2000/|3-2,6|
4500м > 5000м
1000 ≤ 2000/|2,6-1|
1000м >1250м Проверка выполняется, значит, можем спрямить два элемента. Десятый элемент имеет кривую. Подставим значения спрямленных элементов в формулу (3.3): i"c=
Приведенный уклон, для элементов 9-10, вычисляется по формуле (3.4):
ic=-2,6+0,3=-2,3‰.
Элемент 11 - станция Б – этот элемент не спрямляется. На элементе 12 установили наибольший спуск, на котором будет решаться тормозная задача. Спрямляем 13 и 14 элементы по формуле (3.1)
i'c=
Проводим проверку по формуле (3.2):
600 ≤ 2000/|2-1,3|
600м <2857,14м
1200 ≤ 2000/|1,3-1|
1200м < 6666,6м
Проверка выполняется, значит, можем спрямить эти два элемента. Спрямляем 13-14 и 15 элементы по формуле (3.1)
i'c=
Проводим проверку по формуле (3.2):
600 ≤ 2000/|2,2-2| 600м <10000м
1200 ≤ 2000/|2,2-1| 1200м < 1666,6м
1900 ≤ 2000/|3-2,2| 1900м < 2500м
Четырнадцатый элемент имеет кривую. Подставим значения спрямленных элементов в формулу (3.3):
i"c=
Приведенный уклон вычисляется по формуле (3.4):
ic=2,2+0,2=2,4‰.
Проверка выполняется, значит, можем спрямить эти три элемента. Спрямляем 16 и 17 элементы по формуле (3.1)
i'c=
Проводим проверку по формуле (3.2):
4800 ≤ 2000/|8-7,4|
4800м <3333,33м
4800 ≤ 2000/|7,4-3|
4800м < 454,5м
Условие не выполняется, эти два элемента спрямлять нельзя. Элемент 16 переписываем в таблицу. Спрямляем 17 и 18 элементы по формуле (3.1)
i'c=
Проводим проверку по формуле (3.2):
600 ≤ 2000/|3-1,7|
600м <1538,5м
1200 ≤ 2000/|1,7-1|
1200м < 2857,14м
Проверка выполняется, значит, можем спрямить эти три элемента. Восемнадцатый элемент имеет кривую. Подставим значения спрямленных элементов в формулу (3.3):
i"c=
Получили фиктивный подъем. Приведенный уклон считаем по формуле (3.4): ic= -1,7+0,1 =-1,6 ‰
Спрямляем 19 и 20 элементы по формуле (3.1)
i'c=
Проводим проверку по формуле (3.2):
1600 ≤ 2000/|2-1,6|
1600 м < 5000 м
900 ≤ 2000/|1,6-1|
900 м < 3333,33 м
Проверка выполняется, значит можем спрямить эти два элемента. Двадцатый элемент имеет кривую. Подставим значения спрямленных элементов в формулу (3.3):
i"c=
Получили фиктивный подъем. Приведенный уклон считаем по формуле (3.4): ic= 1,6+0,2 =1,8 ‰ Результаты расчетов по спрямлению заданного профиля пути сводятся в таблицу 3.1. Таблица 3.1 – Таблица спрямления профиля пути
Продолжение таблицы 3.1
Поиск по сайту: |
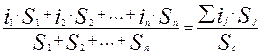 (3.1)
(3.1)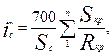 (3.3)
(3.3) 
 ‰.
‰. ‰.
‰. ‰.
‰.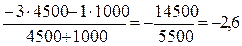 ‰.
‰.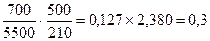 ‰.
‰. ‰.
‰. ‰.
‰. ‰.
‰. ‰.
‰.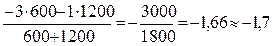 ‰.
‰. ‰.
‰.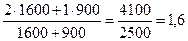 ‰.
‰.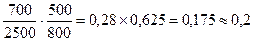 ‰.
‰.